|
Auteur :
WARME R.

Dossier : FORMATEUR


|
|
NOM : ………………………………
|
Prénom : …………………………..
|
Classe :…………………..
|
|
Année scolaire : ………………………
|
Dossier
pris le : ……/………/………
|
Validation
de la formation : O -
N
Le : ……………………………………..
Nom
du formateur : ……………………
|
|
ETABLISSEMENT :
…………………………………………..
|
TITRE :
Calcul numérique et calcul algébrique .
RECHERCHE DE LA VALEUR
NUMERIQUE d’une expression littérale
INFORMATIONS
PEDAGOGIQUES :
|
NIVEAU :
Formation Niveau V
(inclus le CAP et CFA)
|
OBJECTIFS :
- Savoir calculer la valeur numérique d’une
expression algébrique.
- Savoir avec une formule donnée et à partir des valeurs
connues :remplacer les lettres par leur valeur et effectuer le ou les
calculs en vue d’obtenir un résultat .
|
I ) Pré requis: Première
page d’écran interactif
; Cliquer sur « cours ».
II ) ENVIRONNEMENT du
dossier :
III
) LECON
n° 7 RECHERCHE DE LA
VALEUR NUMERIQUE d’une expression
littérale .
Chapitres :
IV) INFORMATIONS
« formation leçon » :
V )
DEVOIRS ( écrits):
* remédiation : ces
documents peuvent être réutilisés ( tout ou partie) pour conclure une formation
.
iNous avons déjà
recherché un résultat en
remplaçant des lettres par des nombres
.lors de la leçon sur les « nombres décimaux
relatifs @ ( voir les derniers exercices de l’évaluation )».
Il est souhaitable de reprendre
ces calculs et pour les mettre en lien ce qui a té fait avec
ce cours .La leçon « sur la recherche d’une valeur numérique d’une expression littérale »
est la suite des calculs avec des
nombres relatifs .
Le but de la leçon « valeur numérique d’une expression
littérale » étant d ’ utiliser des « formules » qui
sont utilisées le cadre professionnel.
Dans le programme il n’est pas
prévu de traiter « normalement » la leçon sur les priorités dans les
calculs .
Pourtant il faut connaître l
’ordre dans lequel on effectuera les
opérations ;: par quelle opération commence t - on ? et par quelle
termine - t - on ? si il y a ( en
partie ou tout ) des additions ,soustractions ,
multiplications ,divisions et puissances voir racine dans une chaîne
d’opérations .
Pré
requis :
|
Leçon
|
LECON
|
|
N°7
|
RECHERCHE DE LA VALEUR NUMERIQUE D’ UNE EXPRESSION
LITTERALE .
|
CHAPITRES :
iEn arithmétique , lorsque
l’on utilise des formules ( voir :calcul d’aire ;
périmètre ….) ; on remplace des lettres par des nombres ( grandeurs) , en
vu de trouver une valeur numérique ; ce
calcul est une activité appelée :
« rechercher la valeur numérique d’une expression littérale » .
Il en est de même si l’on calcule
la valeur numérique d’une expression
algébrique .
Exemples de formules (
expressions littérales ) couramment usitées
Un calcul numérique comporte plusieurs étapes qui, à chaque
fois sont :
-
soit changer l’écriture d’un
nombre.
Exemple : 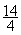 =
= 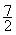 = 3,5
= 3,5
-
soit effectuer une série de transformations grâce à une règle (ou une procédure)
Exemple : 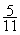 +
+ 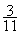 =
= 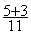 =
=
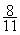
Préambule : Pour
pouvoir effectuer un calcul ou une série de calculs , en vu de trouver un
nombre (appelé : résultat ) , il faut avant tout savoir le lire et donc de connaître les conventions d’écritures
et les priorités opératoires .
En calcul numérique :
· On n’écrit jamais deux signes qui se suivent
sans parenthèses .
on n’écrit
pas 3 ´ - 4 mais
on écrit 3 ´ ( - 4 )
· Au lieu
d’écrire 3 ´ 3 , on écrit 3² ; et 3´ 3´ 3
s’écrit 33
· Le trait de fraction signifie la division du
numérateur par le dénominateur et tout se passe comme si le numérateur et le
dénominateur étaient entre parenthèses.
Ainsi :
* 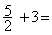 s’écrit
5 ÷ 2 + 3 = ; qui s’écrit
aussi ( 5 ÷ 2 ) + 3
= 5,5
s’écrit
5 ÷ 2 + 3 = ; qui s’écrit
aussi ( 5 ÷ 2 ) + 3
= 5,5
* et 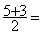 s’écrit
( 5 +3 ) ÷ 2 = ; soit
(8 ) ÷ ( 2 ) = 4
s’écrit
( 5 +3 ) ÷ 2 = ; soit
(8 ) ÷ ( 2 ) = 4
|
i9
|
I.2.
Principales règles de transformations de
l’écriture des nombres
|
:i
|
Il est souvent très utile de transformer les écriture des
nombres et de les remplacer par une valeur numérique. Nous retiendrons les
transformations suivantes :
A) :
@ i 3² signifie 3 ´ 3 (
= 9 ); comme 33 signifie
3´ 3´ 3 ( = 27)
B ) : @ i Le
trait de fraction signifie une division : 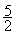 = 2,5
= 2,5
C ) : @ i « simplifier » ; « rendre irréductible » et
« réduire au même dénominateur »
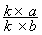 =
= 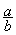
Les nombres « k » et « b » sont des
nombres non nuls . cette écriture permet
de simplifier une fraction
ou de réduire deux
fractions aux mêmes
dénominateurs.
- Simplifier directement les fractions suivantes :
|
Soit la
fraction :
|
On peut
diviser le numérateur et le dénominateur par :
|
On peut
ainsi remplacer : 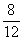
|
|
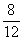
|
« 2 » pour
simplifier ou
« 4 » pour
rendre irréductible .
|
Par
4 / 6 ou 2 / 3
|
-
C 1
) Réduire au même dénominateur 2 fractions :
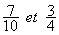 résultat : le dénominateur commun est
« 40 » ;
résultat : le dénominateur commun est
« 40 » ;
les deux fractions équivalentes aux fractions 7 / 10
et 3/ 4 sont 28 / 40 et 30
/ 40
-
C 2
) Réduire au même dénominateur 3
fractions :
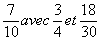 résultat : le
dénominateur commun est
« 60 » ;
résultat : le
dénominateur commun est
« 60 » ;
les
trois fractions équivalentes aux fractions 7 / 10
et 3/ 4 et 18/30 sont 42 / 60 et 45
/ 60 et 36 / 60
D) : @ i L’écriture décimale
et les puissances de dix :
exemples :
a) 0,045 =
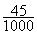 = 45 ´ 10 -3
= 45 ´ 10 -3
b) 0,45 = 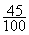 = 45 ´ 10 -2
= 45 ´ 10 -2
E ) :@i L’écriture
décimale et les pourcentages :
exemple : 0,145 = 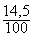 = 14,5
%
= 14,5
%
si la fraction n’est pas
« décimale » ,il faudra :
E 1 ) : @ i- ou
rendre la fraction irréductible .et continuer les calculs avec cette fraction.
E 2 ) : @ i-
ou effectuer la division et
remplacer la fraction par un nombre décimal « arrondi » à
0, ? ? ?1 prés . On remplace le « ? »
par un ou plusieurs« 0 »
F ) : @ i L’écriture 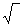 par la
valeur de la racine
par la
valeur de la racine
exemples : on
remplacera 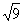 par 3 ;
par 3 ;
et 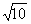 par une valeur approchée » 3,162 )
par une valeur approchée » 3,162 )
le
résultat peut être recherché soit à
partir d’une formule ou d’une chaîne d’opérations possédant ou non des
parenthèses.
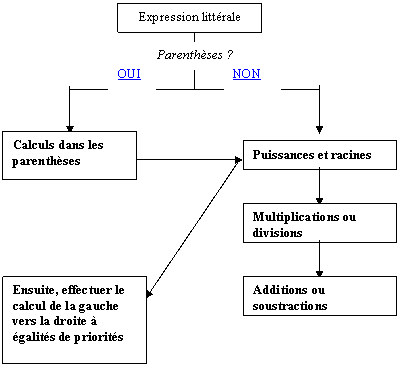
Organigramme concernant l’ordre chronologique des
calculs :
¶ Résultat
numérique recherché à
partir d’un énoncé et d’une formule donnée
Si les calculs s’effectuent
à partir d’une formule donnée :
+Le calcul est direct :
Il n’y a que des
nombres séparés par des signes opératoires dans le deuxième membre , le résultat
s’obtient directement ;on remplace chaque
lettre par leur valeur numérique ,ensuite on effectue les calculs .
Exemple : Calcul d’aire du trapèze (à l’aide de la
formule : 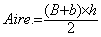 )
)
Application : Un trapèze a les dimensions suivantes :
B = 12,6 cm ; b = 7,4 cm ; h = 6,8 cm.
Calcul de son aire . A = 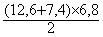 =
68 cm2
=
68 cm2
+Le calcul est
indirect :
L’expérience et les connaissances en algèbre sont
nécessaires ! ! ! ! ! !
Il y a des nombres
dans les deux membres de l’égalité , il y a une lettre dans un des membres ,
qu’il faut isoler . C’est alors un problème d’algèbre : il faut faire
l’inventaire des données numériques , on identifie ce que l’on cherche , on transforme l’égalité
pour isoler l’inconnue , on fait le calcul .
Exemple
: Trouver la hauteur du trapèze qui à une aire de 50 m2 et
dont les bases mesurent 12,6 m et
7,4 m .
Soit la
formule : 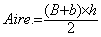 ;
on remplace les lettres par les valeurs données :
;
on remplace les lettres par les valeurs données : 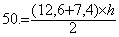
On transforme pour obtenir : h= 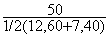 =
=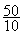 =
5 m
=
5 m
( info @ + :voir le cours sur « résoudre un
problème du premier degré »)
· Résultat
numérique à rechercher à partir
d’une chaîne d’opérations :
Exemple de calculs à
effectuer dans une chaîne d’opérations
L’expression contient
des additions, soustractions
,multiplications ,divisions (ou fractions….) , des puissances , des racines:
Exemple 9,2 - 42  7
+ 2,7
7
+ 2,7  (-6)2 +
(-6)2 + 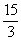 -
- 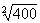 =
=
|
Procédure
|
Exemple
|
|
1ereEtape
|
Calculer
la racine au préalable faire le
calcul sous la racine au cas où…..
|
9,2 - 42  7
+ 2,7 7
+ 2,7  (-6)2 + (-6)2 + 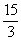 -
20 -
20
|
|
2emeEtape
|
Calculer
les puissances
|
9,2 - 16
 7
+ 2,7 7
+ 2,7  (+36) + (+36) + 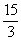 -
20 -
20
|
|
3emeEtape
|
Calculer
les divisions
|
9,2 - 16  7
+ 2,7 7
+ 2,7  (+36) +
5 - 20 (+36) +
5 - 20
|
|
4emeEtape
|
Calculer
les multiplications
|
9,2 - 112 +
(+ 97,2 ) + 5 -
20
|
|
5emeEtape
|
Transformer
l’expression algébrique en somme algébrique
|
(+9,2)+( - 112) + (+ 97,2 ) + (+ 5) + ( - 20)
|
|
6emeEtape
|
Calculer
la somme des nombres positifs
|
(+9,2)+
(+ 97,2 ) + (+ 5) = (+(9,2+97,2+5)= (+
111,4)
|
|
7emeEtape
|
Calculer
la somme des nombres négatifs
|
( - 112) + (
- 20) =( - (112+20)) = (-132)
|
|
8emeEtape
|
Calculer
la somme des nombres de signe contraire
|
(+ 111,4)+ (-132)
= ( - (132- 111,4)) = (-20,6)
|
|
9emeEtape
|
Rendre
compte
|
9,2 - 42  7
+ 2,7 7
+ 2,7  (-6)2 + (-6)2 + 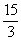 - - 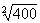 =(-20,6) =(-20,6)
|
ACTIVITES : Calculer (CORRIGE : CLIQUER ICI )
1°) 3 + 5,6 + 8 =
2° ) - 5 - 6,3 -7,2 =
3° ) -8,3 + 5 - 9 - 13,5 + 7,7 =
4°) 15,3 - 4  5,3
+ 7
5,3
+ 7 3
=
3
=
5°) 3, 5 - 9 : 2 + 4 9
=
9
=
6°) -8.4
+ 11 +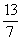
 1,2
=
1,2
=
7 °) 3, 52- 9 : 2 + 4 92
=
92
=
8 ° ) -8,42 + 11 +
(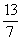 )
2
)
2 1,2 =
1,2 =
9°) 9,2
- 42  7 + 2,7
7 + 2,7  (-6)2 +
(-6)2 + 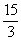 -
- 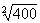 =
=
( info + @ : calculs de……)
|
i9
|
II.
NOTIONS sur le CALCUL ALGEBRIQUE et exemple de résolution de problèmes à
traiter avec l ’ algèbre .
|
Cd info plus
+++
|
i Les objectifs
de base en algèbre qu’il faudra atteindre en fin de niveau V
sont :
- savoir effectuer des calculs qui comportent des
variables ou des inconnues ( notées généralement « x » et
« y ») ; savoir développer et factoriser des expressions ,
- savoir mettre un problème en équation et
- savoir
résoudre des équations ( et système) du premier degré .
Ce cours a pour
but de vous familiariser au vocabulaire qui sera
utilisé dans les objectifs cités ci - dessus .
i Dans les
expressions algébriques le signe
« multiplié » n’est jamais
représenté.
On n’écrit pas les signes ´, sauf entre deux nombres
( pour ne pas confondre entre 24
et 2 ´ 4 )
Exemples :
|
Formule
|
En
omettant les signes ´
|
L’expression
se lit :
|
|
2 ´ p ´ R
|
2p R
|
2 fois
pi fois R
|
|
3´x
|
3x
|
3 fois
ixe
|
|
a´b
|
ab
|
a fois b
|
|
a´b´c
|
abc
|
a fois b fois c
|
|
3´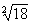
|
3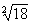
|
3 fois racine carré de 18
|
|
2 ´ x ´ ( 1
- x )
|
2 x (
1 - x )
|
2 fois x
facteur de 1-x
|
|
3 ´ ( 2´ x + 1)
|
3 ( 2x +
1)
|
3
facteur de 2 ixe plus un
|
|
x ´ ( 2´x +2 )
|
x ( 2x +2 )
|
ixe
facteur de 2ixe plus 2
|
|
(2´x +1)´(3´x + 2)
|
(2x+1) (3x+2)
|
2ixe
plus un entre parenthèses facteur
de 3 ixe plus 2.
|
iremarque :
les groupes de mots
« fois entre
parenthèses » et « facteur de » ont la même signification .
êATTENTION au risque d’erreur : ne pas confondre ce qui est dit et de ce qui
est écrit :
Exemple 1 : a +b² est différent de l’écriture ( a + b ) ²
3 + 5
² = 3 + 25 = 28
¹ (3+5)² = 64
Exemple 2 : a - b² est différent de l’écriture ( a -
b ) ² ;
3 -
5² =
3 - 25 =
- 23 ¹ ( 3
-5 )² = 4
A retenir :
Quand on
multiplie un nombre par une lettre ou une parenthèse, on n’écrit pas le signe ´
¶ Calculs @ : tous les calculs peuvent se décomposer en multiplications ,
divisions , additions ou soustraction de monômes ( un monôme est une expression
algébrique qui ne contient ni signe + ni
signe - , c’est un produit de
coefficient et de lettre (s))
Exemples de monômes : 3x ;
2,5 x² ; 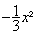
|
On décompose en produit de facteurs et l’on
« regroupe »
|
On regroupe les termes de même degré
|
|
Multiplication de deux monômes
|
Addition ou soustraction de deux monômes de même degré
|
|
Exemple
1 :
5 x²  2x
= 5 2x
= 5 2 2 x x
 x x  x =
10 x3 x =
10 x3
Exemple
2
- 3 x 3  2 x²
= - 3 2 x²
= - 3 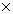 x x
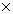 x x x x 2 2 x x x
x
= - 6 2
2 x 5
x 5
= - 12 x 5
|
Exemple 3
5
x² - 2 x² = 3
x²
Exemple
4
4
x² - 3 x² = 1 x²
= x²
|
· Développements et factorisations @
+ Développement @
Définition : Une expression algébrique
est développée si elle est écrite sous la forme
d’une somme de monômes
Les deux modèles mathématiques de base du
développement sont : k ( a + b
) et
k ( a - b )
Exemples :
|
Expressions algébriques de la forme :
|
|
Forme non
développée
|
Forme développée
|
|
k ( a + b )
|
k a + k b
|
|
3 ( x +
5 )
|
3x + 15
|
|
3 ( 2x +
5 )
|
6x + 15
|
|
3 ( x -
5 )
|
3x - 15
|
|
3 ( 2x -
5 )
|
6x - 15
|
Applications :
|
Forme
|
Application numérique
|
Application algébrique :
|
|
k ( a + b)
|
a) 3
( 2 + 5
) = 3 (
7 ) = 3 ´ 7 = 21
b) 3 (
2 +
5 ) = 3 ´ 2 + 3 ´ 5 = 6 +
15 = 21
|
a) 3 ( x
+ 5 ) = 3 ´ x + 3 ´ 5 = 3x
+ 15
b) 3 (
2x +
5 ) = 3 ´2 ´ x + 3 ´ 5 = 6x
+ 15
|
|
k ( a - b )
|
a) 3
( 5 - 2 ) =
3 ( 3 ) = 3 ´ 3 = 9
* b) 3
(5 - 2
) = 3 ´ 5 - 3 ´ 2 = 15
- 6 = 9
|
a) 3 (
x -
5 ) = 3 x - 3 ´ 5 = 3x
- 15
b ) 3 ( 2x
- 5 ) = 3 ´2 ´ x - 3 ´ 5 = 6x
- 15
|
* exemple de développement d’une somme de nombres relatifs :
3
[ (+5 ) + ( -
2 ) ] = 3
(+5 ) + 3 (
- 2 )
= ( +15 )
+ ( - 6 ) = ( + 9 )
Activités :
Développer
2 ( x
+ 3 )
; 7 ( x -
5 ) ; 3 ( 4x + 2,1
) ; 5 ( 3x -
3,2 ) ; x ( x +
1 ) ; x ( 2x + 1 ) ; 2x ( 2x +
1 )
+Suite : Développer ,
réduire, ordonner
@ :
Définition : Une
expression algébrique est développée,
réduite et ordonnée si elle est la somme
de monômes ,de puissances différentes ,ordonnée par puissances décroissantes.
Ordonner :
Exemple d’expression
algébrique ordonnée : A = 7 x² - 3 x + 1
Exemple de l’expression
algébrique ci dessus non-
ordonnée : A = - 3
x + 1 +
7 x²
Réduire : réduire c’est regrouper des termes de même degré ( ou de même
puissance) :
Exemples :
|
Expression « non »
réduite :
|
Expression réduite .
|
|
5 + 3
|
8
|
|
7 - 4
|
3
|
|
x + x
|
2x
|
|
2x + x
|
3 x
|
|
3x + 2 x
|
5 x
|
|
x ² + x ²
|
2 x ²
|
|
3 x + x
|
4 x ²
|
|
Remarque :
on ne peut pas réduire les expressions
ci dessous !
|
|
|
Mais
on peut « factoriser » ! ! ! !à condition de
savoir identifier le « facteur
commun » qui est contenu dans chaque terme . ( info plus +++)
|
|
x ²
+ x ( = x
x + 1 x )
|
= x ( x
+ 1 ) « x » est le facteur commun
|
|
3 +
3 x [ = ( 3 ´ 1 + 3 ´ x ) ]
|
= 3 ( 1 +
x ) « 3 » est le facteur commun
|
|
3 +
x ( il n’y a rien à
modifier)
|
|
Factoriser :
Une expression algébrique est factorisée si elle est écrite sous la forme d’un produit :
A = ( 2x + 1 )²
ou B = 3 ( x + 4 ) ( 3x - 1) ou C
= ( x + 1 ) ( x - 1 )
Pour savoir factoriser il faut savoir identifier les
termes qui contiennent un facteur commun
. ( info plus +++)
On dit aussi que
pour « factoriser » il faut
savoir identifier dans les termes de
l’expression algébrique le (ou les )
facteur commun .
i Pour factoriser
ou développer on utilise les égalités :
k ( a + b ) = k a + k b
(
a + b ) ( c + d ) = a c + ad + b c + bd
ou les Identités
Remarquables .
Pour informations :
les I.R. sont des « outils mathématiques » , elles se présentent sous « 3 formes » , elles sont
utilisées soit pour donner une forme
factorisée ou inversement donner une
forme développée d’une expression algébrique du « second degré » .
|
Modèles
théoriques :
( le deuxième membre
est obtenu après avoir développé , et réduit et ordonné le développement .)
|
Applications ( exemples) : où il faut
successivement : développer ,
réduire et ordonner
|
|
1ère
forme :
La
forme ( a + b )2 qui s’écrit aussi ( a + b ) (a + b) donne
l’égalité de la forme :
( a + b )2 = a2 + 2ab + b2
|
a) ainsi
( x + 1 ) 2 qui s’écrit
( x +1 ) ( x + 1 ) donne l’égalité :
(x + 1 ) 2 = x2
+ 2 x +1
b) et ( 3x + 2 ) 2 s’écrit ( 3x + 2 ) ( 3x + 2 ) donne
l’égalité :
(3x + 2 ) 2 =
(3x)2 +2 fois 3x fois 2
+22
= 9 x²
+ 12 x + 4
|
|
2ème forme :
La
forme ( a - b )2 qui s’écrit aussi ( a - b ) (a - b ) donne
l’égalité de la forme :
( a - b) 2 =
a2 – 2ab + b2
|
a) ainsi : ( x - 1 ) 2 s’écrit
( x - 1 ) ( x - 1 ) :pour donner
l’égalité :
(x - 1 ) 2 = x2
- 2 x +1
b) et ( 3x - 2 ) 2 s’écrit
( 3x - 2 ) ( 3x - 2 ) et donne
l’égalité suivante :
(3x - 2 ) 2 =
(3x)2 -2 fois 3x fois 2
+ 22
= 9 x²
- 12 x + 4
|
|
3ème forme :
*La forme ( a + b ) ( a - b ) qui s’écrit
( a - b ) ( a +b ) donne l’égalité de la forme :
( a - b ) ( a +b ) = a2 – b2
|
a) ainsi
( 3x + 2 ) ( 3x - 2 ) = ( 3x )2 - 22 = 9x² - 4
b) (x - 1 ) 2 = x2
-1
|
·
les égalités en caractère gras
seront à retenir et utilisées dans le cadre du calcul mental .
·
exemples : ( 101) ² ( =
100 + 1 ) ²; 49 ² ( = 50 - 1 ) ² ; ………
iPour
effectuer une opération (calcul) il faut
deux nombres. Lorsqu’il y a plus de deux nombres, il y a au moins deux
opérations à effectuer, il y a souvent
une opération à faire avant l’autre, on
dit que la première opération à priorité sur la seconde opération.
Les 3 principales priorités sont :
+Si il y a des parenthèses :on effectue en
premier les calculs entre ces parenthèses.
Exemple : 2 ( L + l )
= ; on calcule d’abord la somme : L + l puis on multiplie par cette somme
par 2 .
Tout comme il est possible de
développer : 2 ( L + l ) = 2
L +
2 l
+Une puissance à priorité sur la multiplication.
Exemple : 3,14 R²
: on calcule d’abord
R² ;puis on multiplie le résultat par 3,14 .
+La multiplication et la division sont prioritaires
sur l’addition et la soustraction.
Exemple : 3 + 4
l ; on calcule 4 fois « l »
puis on ajoute « 3 »
A ) Exemple d’utilisation d’une formule
|
On donne
les dimensions du trapèze B = 8 ; b
= 5
et h = 4 ( les unités sont des
, par exemple, cm)
On veut
connaître son aire .
On connaît
la formule : A = 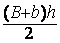
|
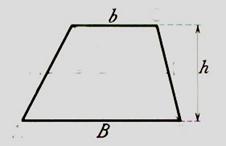
|
|
¬ On remplace les lettres par leurs valeurs : A
= 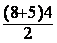
On calcule dans les parenthèses : A = 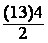
® Puis on calcule
(13)4 = 4 ( 13) = 4 13 = 52 ainsi : A =
13 = 52 ainsi : A = 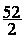
¯ On divise :
52 :2 ainsi A = 26
°On conclue : l’aire du trapèze est de 26 cm²
|
B ) Exemples de calculs : ou il faut
remplacer les lettres par des valeurs numériques et calculer :
|
N°1 ) Soit l’expression littérale :
|
4a + 5 b –
2c
|
Calculer
sa valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation
de l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
4 3
+ 5 3
+ 5 8 – 2
8 – 2 5
= 5
=
|
42
|
|
2°)
|
4,3
|
9,25
|
1,5
|
4 4,3
+ 5 4,3
+ 5 9,25
– 2 9,25
– 2 1,5
= 1,5
=
17,2 + 46,25 - 3
|
60,45
|
|
3°)
|
-4
|
+6
|
-8
|
4 (-4)
+ 5 (-4)
+ 5 (+6) – 2
(+6) – 2 (-8)= (-8)=
-16 + 30 –
(-16) =-16 +30 + (+16)
|
( +30)
|
|
N°2 :Soit l’expression littérale :
|
4a² + 5 b ´ 2c
|
Calculer
sa valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation
de l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
4 3²
+ 5 3²
+ 5 8
8  2 2 5
= 36 + 400 5
= 36 + 400
|
436
|
|
2°)
|
4,3
|
9,25
|
1,5
|
4 4,3²
+ 5 4,3²
+ 5 9,25 9,25
 2 2 1,5
= 1,5
=
73,96 +
|
212,71
|
|
3°)
|
-4
|
+6
|
-8
|
4 (-4)²
+ 5 (-4)²
+ 5 (+6)
(+6)  2 2 (-8)= (-8)=
64 + ( - 480 ) =
|
- 416
|
|
N°3 :Soit l’expression littérale :
|
4a + ( 5 b
– 2c )²
|
Calculer sa
valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation
de l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
4 3
+ ( 5 3
+ ( 5 8 – 2
8 – 2 5)
² = 5)
² =
|
912
|
|
2°)
|
4,3
|
9,25
|
1,5
|
4 4,3
+ ( 5 4,3
+ ( 5 9,25
– 2 9,25
– 2 1,5)²
= 1,5)²
=
17,2 + 612,5625
|
629,5625
|
|
3°)
|
-4
|
+6
|
-8
|
4 (-4)
+ (5 (-4)
+ (5 (+6) – 2
(+6) – 2 (-8))²= (-8))²=
- 16
+ 2116 =
|
2100
|
|
N° 4 :Soit l’expression littérale :
|
4a + ( 5 b
– 2c )²
|
Calculer
sa valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation
de l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
4 3
+ ( 5 3
+ ( 5 8 – 2
8 – 2 5)
² = 5)
² =
|
912
|
|
2°)
|
4,3
|
9,25
|
1,5
|
4 4,3
+ ( 5 4,3
+ ( 5 9,25
– 2 9,25
– 2 1,5)²
= 1,5)²
=
17,2 + 612,5625
|
629,5625
|
|
3°)
|
-4
|
+6
|
-8
|
4 (-4)
+ (5 (-4)
+ (5 (+6) – 2
(+6) – 2 (-8))²= (-8))²=
- 16
+ 2116 =
|
2100
|
|
N°5 :Soit l’expression littérale :
|
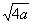 + 5 + 5 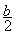 – (2
c ) ² – (2
c ) ²
|
Calculer
sa valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation
de l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
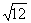 + 5 + 5 4 – ( 10 ) ² = 2
4 – ( 10 ) ² = 2 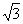 + 20 - 100 = + 20 - 100 =
= 2 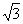 - 80 - 80
|
= 2 ( - 40 + 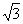 ) )
|
|
2°)
|
-4
|
+6
|
-8
|
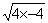 + 5 fois + 5 fois 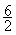 – (2
-8 ) ² : résultat terminal
impossible – (2
-8 ) ² : résultat terminal
impossible
|
Le calcul n’est pas possible pour 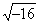
|
CONSEILS :
Après une première lecture : il faut prendre les
travaux auto formatifs, et travailler chapitre par chapitre.
Surtout , allez au « corriger » pour vérifier vos
réponses.
Si le devoir « contrôle » paraît long, passer le
en plusieurs fois.
|
TRAVAUX N°7
d ’ AUTO - FORMATION : CONTROLE
|
|
1°) Compléter la phrase suivante :
Pour calculer la valeur numérique d’une expression littérale
, on remplace …………………………….. qui lui
sont attribuées (données) .
2°) A quel
calcul correspond les formules
suivantes :
|
Formules
|
Permet de calculer :
|
|
A = c²
|
|
|
P =4c
|
|
|
P = 2pR
|
|
|
A = pR² avec
(p » 3,14 )
|
|
|
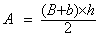
|
|
|
P = 2 (
L + l )
|
|
|
A = L l l
|
|
|
A = 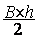
|
|
Compléter la
phrase : un calcul numérique comporte
une ou plusieurs étapes qui , à chaque fois sont :
1°) On n’écrit jamais
deux signes qui se suivent ……………………. .
2°) Au lieu d’écrire 3 ´ 3 , on écrit ……………. ;
3°) Au lieu d’écrire
3´ 3´ 3
s’écrit ………………..
4°) Le trait de
fraction signifie ………………… du ………………………………………. et tout se passe comme si le
numérateur et le dénominateur étaient entre parenthèses.
I.2. Principales règles de transformations de
l’écriture des nombres
Transformer les écritures suivantes :
%Ï 3² signifie ………………… ; comme 33 signifie ……………………
%Ï Le trait de fraction signifie
une division : 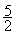 = …………. ;
= …………. ; 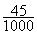 = ………… ;
= ………… ; 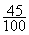 = ……..
= ……..
%Ï 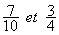 réduire au
même dénominateur commun …………………………………
réduire au
même dénominateur commun …………………………………
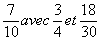 résultat : dénominateur commun
……………………………………….
résultat : dénominateur commun
……………………………………….
%Ï écrire sous forme décimale :
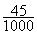 = ……………
= ……………
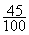 = ………………..
= ………………..
45 ´ 10 -3 = ……………
45 ´ 10 -2 = …………………
%Ï écrire 14,5 % sous forme de fraction = ……………et sous
forme décimale =…….:
%Ï rendre
la fraction irréductible . : 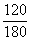 =
=
%Ï effectuer la
division 2 ¸ 3 et remplacer la fraction par un nombre
décimal « arrondi » à 0, 01 prés . 2 / 3
=
%Ï Donner la valeur
de la racine : à 0,01 prés .
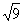 =
=
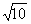 =
=
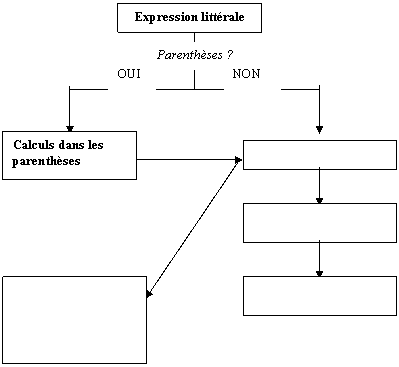
Compléter l’organigramme suivant
avec les mots : Additions ou
soustractions, Multiplications ou
divisions , Puissances et racines ,
Ensuite, effectuer le calcul de la gauche vers la droite à égalités de
priorités
2°) Calcul
à la lecture d’un énoncé et d’une formule donnée
Si les
calculs s’effectuent à partir d’une
formule donnée :
a) A quelle condition dit-on que le calcul est direct ?
b) Quand
dit - on que le calcul est
indirect ? que faut - il faire ?:
Evaluation :
Application 1 : Calcul d’aire du trapèze
( formule : 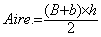 )
)
Un trapèze a les dimensions suivantes : B = 12,6
cm ; b = 7,4 cm ; h = 6,8 cm.
Calcul de son aire .
Application 2 : Trouver la hauteur du trapèze qui à une aire
de 50 m2 et dont les bases mesurent 12,6 m et 7,4 m .
Soit la
formule : 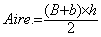 ;
;
Contrôle : On donne une chaîne de nombres contenant
les opérations suivantes :
des additions, soustractions
,multiplications ,divisions (ou fractions….) , des puissances , des racines.
Donnez la procédure ( en 9 étapes maximales) à appliquer
pour parvenir au résultat.
Par
l’exemple suivant 9,2 - 42  7
+ 2,7
7
+ 2,7  (-6)2 +
(-6)2 + 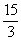 -
- 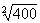 =
=
Série :
Calculer
Faire les calculs suivants en
indiquant les étapes intermédiaires:
1°) il n'y a que des
additions :
3 + 5,6 + 8 =
2° ) il n'y a que des
soustractions :
- 5 - 6,3 -7,2 =
3° ) il n'y a que des additions et
des soustractions :
-8,3 + 5 - 9 - 13,5 + 7,7 =
4°) il n'y a que des additions;
des soustractions ;des multiplications :
15,3 - 4  5,3
+ 7
5,3
+ 7 3
=
3
=
5°) il n'y a que des additions;
des soustractions ;des multiplications
et des division (ou fractions)
3, 5 - 9 : 2 + 4 9
=
9
=
6°) -8.4 +
11 +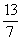
 1,2
=
1,2
=
7°) il n'y a que des additions, soustractions ,multiplications
,divisions , des puissances .
3, 52- 9 : 2 + 4 92
=
92
=
8° ) -8,42 + 11 +
(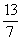 )
2
)
2 1,2 =
1,2 =
9°)Que des
additions, soustractions ,multiplications ,divisions , des puissances
et des racines .
|
II. NOTIONS sur le CALCUL ALGEBRIQUE et exemple de résolution de problèmes en
algèbre
|
Cd info plus +++
|
1°) Compléter la
phrase :
Dans les expressions algébriques le signe « ………………… »
n’est jamais représenté.
2°) écrire les
formules ( 1 ) en utilisant la
convention précédente .
|
Formules
( 1 )
|
Ecritures
normalisée .
|
|
2 ´ p ´ R
|
|
|
3´x
|
|
|
a´b
|
|
|
a´b´c
|
|
|
3´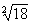
|
|
|
´ x ´ ( 1
- x )
|
|
|
3 ´ ( 2´ x + 1)
|
|
|
x ´ ( 2´x +2 )
|
|
|
(2´x +1)´(3´x + 2)
|
|
3 °): remplacer le groupe de mots « fois entre parenthèses » par un mot qui ( synonyme ) a la même signification :
« ………………… »
4°) traduire
« a » plus « b » au carré : …………………
5°)
traduire « a » plus
« b » entre parenthèses , au
carré . : ……………..
6°) traduire
« a » moins
« b » au carré : ……………….
7°) traduire « a » moins « b » entre
parenthèses , au carré . : ………………
8°) Calculer et commenter :
3
+ 5 ² = ………………………….
(3+5)² = …………………………..
conclusion : 3 + 5 ² est
……………… de (¹) (3+5)²
9°) Calculer et commenter :
3 - 5² =
-……………..
( 3 -5 )²
= ……………
conclusion : 3 - 5 ²
est ……………… de (¹) ( 3 - 5
)²
10 ° ) Quand on multiplie un nombre par une
lettre ou une parenthèse, on n’écrit pas le signe : ´
1°)
compléter la phrase :
tous les
calculs (résultats) peuvent se
décomposer en ……………………………………………..
…………………………………………………………………………………………………….
2°) regrouper les facteurs :
a): 5 x²  2x
=
2x
=
b) -3 x 3  2 x²
=
2 x²
=
3°) regrouper les termes :
a) 5 x²
- 2 x² =
b) 4 x²
- 3 x² =
· Développements et factorisations
a)
Développement : compléter la définition
Définition : Une expression algébrique
est développée si elle est écrite sous la forme
……………………. de monômes .
b) Quels sont les deux modèles mathématiques de base du
développement ?
Exercices : donner la forme développer des expressions suivantes
.
|
Forme non développée
|
Forme développée
|
|
k ( a + b )
|
|
|
3 ( x +
5 )
|
|
|
3 ( 2x +
5 )
|
|
|
k ( a - b )
|
|
|
3 ( x -
5 )
|
|
|
3 ( 2x -
5 )
|
|
|
3 [ (+5 ) + (
- 2 ) ]
|
|
|
Suite Activités :
|
|
|
2 ( x +
3 )
|
|
|
7 ( x -
5 )
|
|
|
3 ( 4x +
2,1 )
|
|
|
5 ( 3x - 3,2
)
|
|
|
x ( x + 1
)
|
|
|
x ( 2x
+ 1 )
|
|
|
2x ( 2x
+ 1 )
|
|
+Suite : Développer , réduire,
ordonner :
compléter
la phrase suivante :
Définition : Une expression
algébrique est développée, réduite et ordonnée si
elle est ……………………………………………………………………………………………………
Exercice :
Voici 3 expressions ; laquelle
est ordonnée ?
|
A = -
3 x + 1 + 7 x²
|
A
= +1
- 3 x + 7 x²
|
A
= 7 x² - 3 x + 1
|
Réduire :
Que
signifie « réduire » ?
Exercices :
réduire les expression suivantes .
|
Expression « non »
réduite :
|
Expression réduite .
|
|
5 + 3
|
|
|
7 - 4
|
|
|
x
+ x
|
|
|
2x + x
|
|
|
3x +
2 x
|
|
|
x ²
+ x ²
|
|
|
3 x ²
+ x²
|
|
Factoriser :
Quand dit - t - on
qu’une expression algébrique est
factorisée ?
Que faut - il identifier dans les termes d’une expression algébrique
avant de factoriser ?
Exercices : Factoriser
les expressions suivantes :
|
x
² + x
( = x x + 1 x )
|
|
|
3
+ 3 x [ =
( 3 ´ 1 + 3
´ x ) ]
|
|
|
3
+ x ( il n’y a rien à modifier)
|
|
Les
I.R. Donner les trois formes des égalités
concernant les Identités remarquables :
Exercices :
En vous aidant de ces égalités ; appliquez les aux exercices
suivants :
|
(x - 1
) 2 =
|
|
|
|
(3x -
2 ) 2 =
|
|
|
|
(3x +
2 ) 2 =
|
|
|
|
(x - 1
) 2 =
|
|
|
|
( 3x +
2 ) ( 3x - 2 ) =
|
|
|
|
(x + 1
) 2 =
|
|
|
1°) Citer les trois grandes priorités :
Calculer :
|
3 + 5 ²
=
|
|
|
( 3 +5 )² =
|
|
|
3 -5² =
|
|
|
( 3 -5 )²
=
|
|
Réponses :
28 ; 64 ;-23 ;4
Série
1 :
B ) Exemples
de calculs : ou il faut remplacer les lettres par des valeurs numériques
et calculer :
|
N°1 ) Soit l’expression littérale :
|
4a + 5 b – 2c
|
Calculer sa valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation de
l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
|
|
|
2°)
|
4,3
|
9,25
|
1,5
|
|
|
|
3°)
|
-4
|
+6
|
-8
|
|
|
|
N°2 :Soit l’expression littérale :
|
4a² + 5 b ´ 2c
|
Calculer sa valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation de
l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
|
|
|
2°)
|
4,3
|
9,25
|
1,5
|
|
|
|
3°)
|
-4
|
+6
|
-8
|
|
|
|
N°3 :Soit l’expression littérale :
|
4a + ( 5 b – 2c )²
|
Calculer sa valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation de
l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
|
|
|
2°)
|
4,3
|
9,25
|
1,5
|
|
|
|
3°)
|
-4
|
+6
|
-8
|
|
|
|
N°4 :Soit l’expression littérale :
|
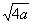 + 5 + 5 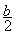 – (2
c ) ² – (2
c ) ²
|
Calculer sa valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation de
l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
|
|
|
2°)
|
-4
|
+6
|
-8
|
|
|
SERIE 2 :
|
N°1 :Soit l’expression
littérale :
|
7a + 8,5 b
|
Calculer sa valeur numérique :
|
|
« a »
|
« b »
|
Transformation de
l’expression
|
Résultat
|
|
1°)
|
6
|
2
|
|
|
|
2°)
|
( + 6)
|
( +2)
|
|
|
|
3°)
|
( +6 )
|
( - 2 )
|
|
|
|
4°)
|
( - 6 )
|
( - 2)
|
|
|
|
5°)
|
( - 6 )
|
( + 2)
|
|
|
|
N°2 :Soit l’expression
littérale :
|
5a - 10 b
|
Calculer sa valeur numérique :
|
|
« a »
|
« b »
|
Transformation de
l’expression
|
Résultat
|
|
1°)
|
6
|
2
|
|
|
|
2°)
|
( + 6)
|
( +2)
|
|
|
|
3°)
|
( +6 )
|
( - 2 )
|
|
|
|
4°)
|
( - 6 )
|
( - 2)
|
|
|
|
5°)
|
( - 6 )
|
( + 2)
|
|
|
|
N°3 :Soit l’expression
littérale :
|
2 m  5
n 5
n
|
Calculer sa valeur numérique :
|
|
« a »
|
« b »
|
Transformation de
l’expression
|
Résultat
|
|
1°)
|
15,5
|
2,6
|
|
|
|
2°)
|
( + 5)
|
( + 3)
|
|
|
|
3°)
|
( +6,1 )
|
( - 2,3 )
|
|
|
|
4°)
|
( - 0,6 )
|
( - 0,2)
|
|
|
|
N°4 :Soit l’expression
littérale :
|
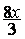 + 11,5 + 11,5
|
Calculer sa valeur numérique :
|
|
« x »
|
|
Transformation de
l’expression
|
Résultat
|
|
1°)
|
6
|
|
|
|
|
2°)
|
( + 9)
|
|
|
|
|
3°)
|
( -3)
|
|
|
|
|
N°5 :Soit l’expression
littérale :
|
4a + 5 b – 2c
|
Calculer sa valeur numérique :
|
|
« a »
|
« b »
|
« c »
|
Transformation de
l’expression
|
Résultat
|
|
1°)
|
3
|
8
|
5
|
|
|
|
2°)
|
4,3
|
9,25
|
1,5
|
|
|
|
3°)
|
-4
|
+6
|
-8
|
|
|
SERIE 3
|
Formules :
|
Calculs :
|
Si
pb : voir « résoudre une équation.
|
|
A = c²
|
c = 5,6 , calculer A =
|
A = 121 ; calculer c =
|
|
P
=4c
|
C =
60 ; calculer P=
|
P = 51,6 ; calculer c =
|
|
P =
2pR
(p » 3,14 )
|
R = 2,5 ; calculer P=
|
P = 47,1 ; calculer R =
|
|
A =
pR² avec
(p » 3,14 )
|
R = 3 ; calculer A =
|
A = 100,48 calculer
R =
|
|
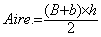
|
B = 4 ; b = 3 ; h = 2,5
Calculer l’Aire =
|
|
|
P =
2 ( L + l )
|
L = 12 ; l
= 5,6
Calculer P =
|
|
|
A =
L l l
|
L = 12 ; l
= 5,6 ; calculer A =
|
|
|
A =
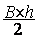
|
B = 4 ; b = 3
calculer A =
|
|
SERIE 4 :
Pour travailler la leçon sur le « repérage » il est conseillé
de savoir faire les calculs ci-dessous :
|
LES FONCTIONS : ( pré requis )
|
|
A partir des explications précédentes
remplir les tableau x suivants : Ces calculs suivants seront
réutilisés pour faire la
représentation graphique de chaque
fonction.
|
1°) Compléter le tableau pour f1(x) = 2,5 x
, et placer ces points dans le repère cartésien .
|
x
|
0
|
0,5
|
1
|
1,5
|
2
|
2,5
|
3
|
3,5
|
4
|
|
f1(x)
|
|
|
|
|
|
|
|
|
|
2°) Compléter le tableau suivant:
f2(x) = x -
1
|
x
|
0
|
0,2
|
0,5
|
0,8
|
1
|
2
|
3
|
4
|
5
|
|
f2(x)
|
|
|
|
|
|
|
|
|
|
3°) soit l’équation f3(x) = -2x + 0,5
, Compléter le tableau suivant:
|
x
|
0
|
-0,2
|
-0,5
|
-0,8
|
-1
|
-2
|
-3
|
-4
|
-5
|
|
f3(x)
|
|
|
|
|
|
|
|
|
|
4°) Compléter le tableau
pour f 4(x) = � 0,5x
|
x
|
0
|
-0,2
|
-0,5
|
-0,8
|
-1
|
-2
|
-3
|
-4
|
-5
|
|
f 4(x)
|
|
|
|
|
|
|
|
|
|
5°) Dans le même repère faire le tracé des fonctions
f1 = y1 ;
f2= y2 ; f3=
y3 et y4 = f4, ,
telles que f1(x) = x2 f2(x) = 3 x2 , f3(x) = - 2x2 et
f 4(x) = �0,5 x2 +1
Au préalable compléter le tableau suivant:
|
x
|
0
|
-0,2
|
-0,5
|
-0,8
|
-1
|
-2
|
-3
|
-4
|
-5
|
|
f1(x)
|
|
|
|
|
|
|
|
|
|
|
f2(x)
|
|
|
|
|
|
|
|
|
|
|
f3(x)
|
|
|
|
|
|
|
|
|
|
|
f 4(x)
|
|
|
|
|
|
|
|
|
|
![]() =
= ![]() = 3,5
= 3,5![]() +
+ ![]() =
= ![]() =
=
![]()
![]() s’écrit
5 ÷ 2 + 3 = ; qui s’écrit
aussi ( 5 ÷ 2 ) + 3
= 5,5
s’écrit
5 ÷ 2 + 3 = ; qui s’écrit
aussi ( 5 ÷ 2 ) + 3
= 5,5 ![]() s’écrit
( 5 +3 ) ÷ 2 = ; soit
(8 ) ÷ ( 2 ) = 4
s’écrit
( 5 +3 ) ÷ 2 = ; soit
(8 ) ÷ ( 2 ) = 4![]() = 2,5
= 2,5![]() =
= ![]()
![]() résultat : le dénominateur commun est
« 40 » ;
résultat : le dénominateur commun est
« 40 » ; ![]() résultat : le
dénominateur commun est
« 60 » ;
résultat : le
dénominateur commun est
« 60 » ;![]() = 45 ´ 10 -2
= 45 ´ 10 -2![]() = 14,5
%
= 14,5
%![]() par la
valeur de la racine
par la
valeur de la racine ![]() par 3 ;
par 3 ;![]() par une valeur approchée » 3,162 )
par une valeur approchée » 3,162 ) 
![]() )
)![]() =
68 cm2
=
68 cm2![]() ;
on remplace les lettres par les valeurs données :
;
on remplace les lettres par les valeurs données : ![]()
![]() =
=![]() =
5 m
=
5 m![]() 7
+ 2,7
7
+ 2,7 ![]() (-6)2 +
(-6)2 + ![]() -
- ![]() =
=![]() 5,3
+ 7
5,3
+ 7![]() 3
=
3
=![]() 9
=
9
= ![]()
![]() 1,2
=
1,2
=![]() 92
=
92
= ![]() )
2
)
2![]() 1,2 =
1,2 =![]() 7 + 2,7
7 + 2,7 ![]() (-6)2 +
(-6)2 + ![]() -
- ![]() =
=



