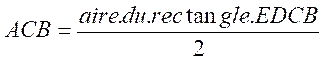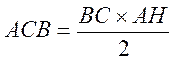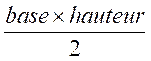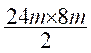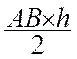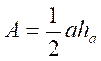1.     Le triangle quelconque ( découverte des notions)

2.     L’aire d’un parallélogramme

3.     Les unités d’aire

4.     Le triangle scalène ( caractéristiques )

Index  

Objectif précédent :

Aire et surface (notion)    

Objectif suivant :

Aire d’un triangle quelconque dont on connaît un angle et une longueur d’un côté.

tableau   

1°) informations sur les triangles      

2°) tout sur les aires 

DOSSIER : Aire du triangle quelconque (scaléne) dont on connaît une longueur  d’un côté et celle de la hauteur associée.

Exercice préliminaire .

Définitions : base , sommet , hauteur .

Formule(s) .

 Aire de triangles de même base et de même hauteur .

Aire d’un triangle quelconque .

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle 

Corrigé évaluation 

Travaux  niv. VI : dos 119

Devoir :

COURS

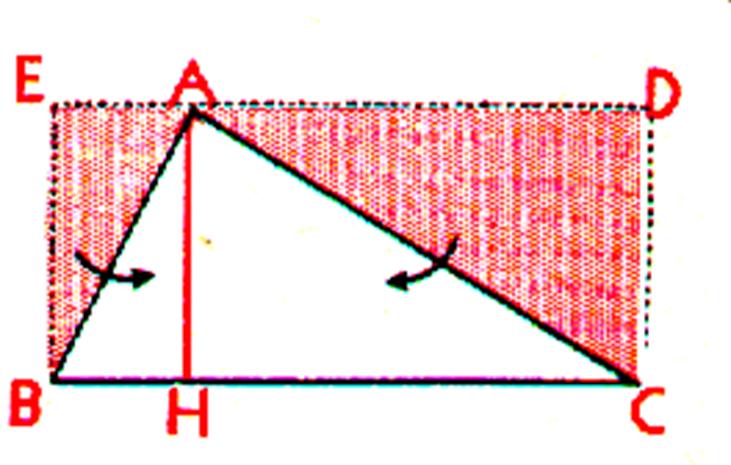
Exercice préliminaire :

Soit un triangle quelconque BAC. Si nous menons aux points  B et C les perpendiculaires au coté BC , ces perpendiculaires forment avec la parallèle menée par le point A , au côté BC , un rectangle EDCB.

Par ailleurs , la hauteur AH décompose le triangle  BAC en deux triangles rectangles BAH et ACH qui sont respectivement égaux aux triangles rectangles EAB et ADC ; en effet , si nous décalquons le triangle EAB , il est facile de vérifier que ce triangle est superposable au triangle AHB ; on vérifie également avec un calque que les triangles rectangulaires ACH et ADC sont superposables donc égaux.

L’aire du triangle  ACB est la moitié de l’aire du rectangle EDCB , nous pouvons en effet écrire :

Aire rectangle EDCB = 2 aires triangle AHB + 2  aires triangle ACH

Aire triangle ACB = aire du triangle AHB + aire du triangle ACH.

Donc aire triangle

Or aire EDCB = BC AH

Donc Aire

Quelques rappels :

-  « Nature du triangle » : le triangle est une figure plane limitée par trois lignes droites qui en sont les côtés .

-    Dans tout triangle il y a un double élément à considérer : les côtés et les angles

-  Les angles sont formés par la plus ou moins grande ouverture des côtés ; l’un d’eux peut être droit ou obtus ; les autres sont nécessairement aigus . Leur somme égale deux droits.

Définitions : base , sommet , hauteur .

                La « base » du triangle est le côté sur lequel il  est censé posé . On peut prendre pour base l’un  quelconque des côtés.

               Le « sommet » est un point  de rencontre des deux autres côtés .

               La  « hauteur » est la perpendiculaire abaissé  du sommet sur la base ou sur son prolongement

A savoir :

L ‘ aire d’un triangle est égale au produit de la longueur de la base par la longueur de la hauteur ,le produit divisé par deux.

Remarque : les longueurs doivent être exprimées dans la même unité de longueur

INF0 PLUS +++++

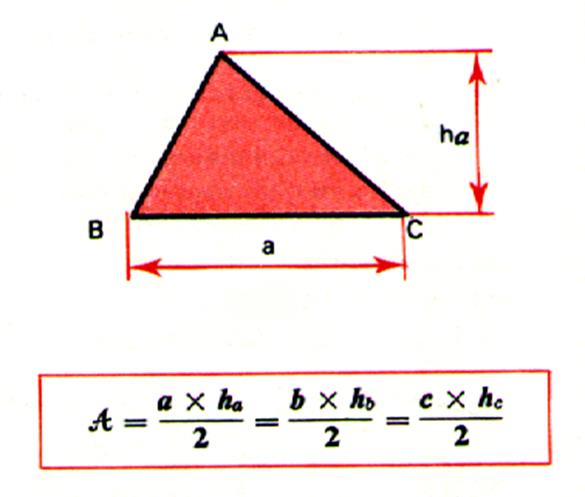
Formule(s) :

Aire =

Application : quelle est l’aire de la surface d’un triangle qui à 24 m de base et 8 m de hauteur .

S =          =                  = 96 m²

Aire des triangles particuliers:

·      Triangle rectangle

·      Triangle isocèle

·      Triangle équilatérale

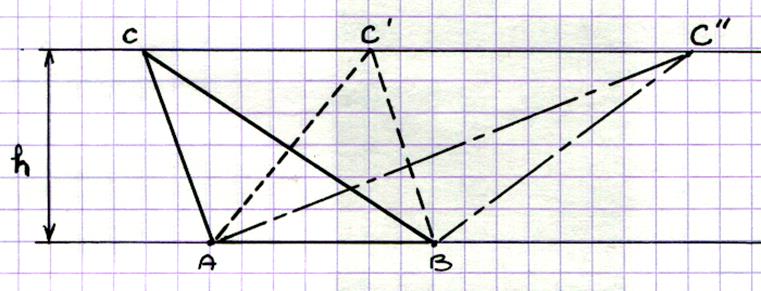
Aire de triangles de même base et de même hauteur :

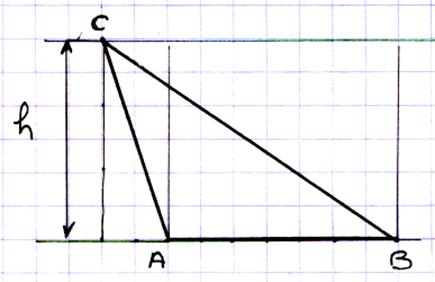
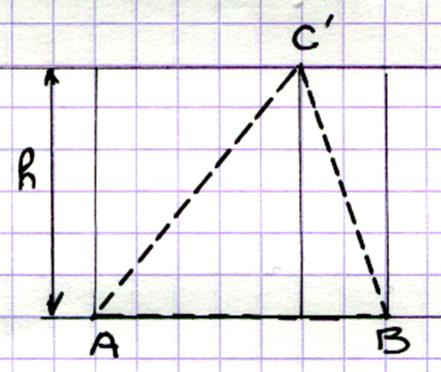
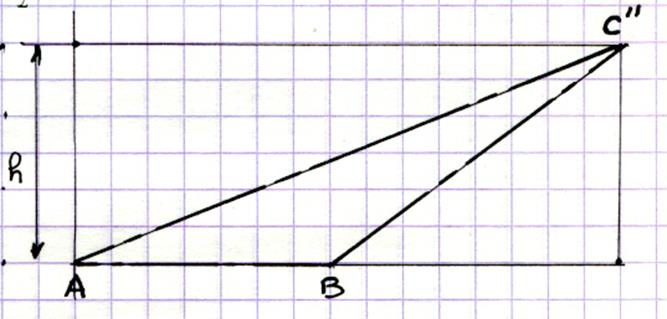
Soit 3 triangles ACB ; AC’B ; AC’’B

On donne  d(A,B)= 3,5  et h =  3

En faisant le calcul d’aire pour chaque triangle , on peut conclure que les triangles ont la même aire .

Tracer ces triangles sur une feuille quadrillée ; compter les carreaux .

Réalisons :

1°) Calcul  de l’aire du triangle ABC :                                       Aire =

2°) Calcul  de l’aire du triangle AC’B :

Aire =

3°) Calcul  de l’aire du triangle AC’’B :

Aire =

Conclusion :  si  3 triangles qui ont la même base et la même hauteur , ils ont la même aire .

Info plus : démonstration du théorème de Pythagore

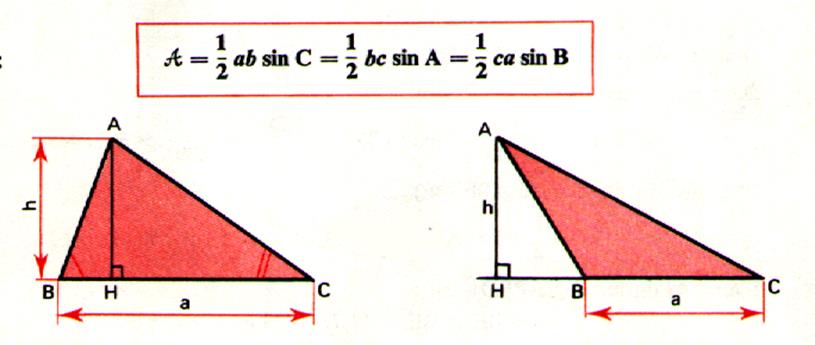
Aire d’un triangle quelconque : ( SOS cours :en faisant intervenir les sinus d’un angle)

AH =   h_a

AB sin. =AC sin

 h_a = c sin  = b sin

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1 ) A quoi est égale l’ aire du triangle  ?

2 ) Donner la formule permettant de calculer l’aire d’un triangle scalène (compléter avec un dessin coté )

EVALUATION

1°) la base d’un triangle mesure   15 cm ; la hauteur 8 cm.

      Calculer son aire.

INTERDISCIPLINARITE

Série 1

1 ) Un pré de forme triangulaire a 42 dam de base et 285m de hauteur . Exprimer son aire en ares.

2 )  Un champ a la forme d’un triangle rectangle . Les deux côtés de l’angle droit ont l’un 88,50 m et l’autre 124 m . quel est son aire , en ares ?

3 )  Un triangle  a une mesure de  108 m² et 12 m de hauteur . quelle est la longueur  de sa base ?

Série 2.

4°) Un jardin de forme triangulaire a une base mesurant 48 m et une hauteur  mesurant 32 m. Quelle est son aire en m² ?

5°) Les côtés de l’angle droit d’un parterre en forme de triangle rectangle mesurent 56 dm  et 4,5 m . Quelle est son aire en m² ?

6°) Un triangle a une aire de 18 00 cm² . Sa base est de 75 cm . Quelle est la mesure de sa hauteur en cm ?

Série 3 .

7°)  Un terrain de forme de triangle rectangle a ses côtés de l’angle droit qui mesure 76 m et 45 m . Quelle son aire, en ha ?

8°) Un triangle a une aire de 0,045 m² .Sa hauteur mesure 25 cm . Quelle est en cl la mesure de sa base ?

9°) Une tôle triangulaire mesure 265 mm de base et 34cm de hauteur. Calculer son aire en cm² ( arrondir à 1 prés par défaut)