Module : PERIMETRE et AIRE Géométrie		DOSSIER : 119
warmaths ; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI
Info conseils et consignes.	TRAVAUX NORMATIFS PRIMAIRE / COLLEGE Matière : MATHEMATIQUES.		Pré requis : dos 118 Corrigé @
AIRE du TRIANGLE QUELCONQUE
Info 1 @ cours aires des triangles quelconques : ; Info 2 @ cours  surface d’ un triangle quelconque : ; Classe de collège 5^ème : les calculs d’aire.
TRAVAUX CONTROLE
Doc WR
Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours .
INFO COURS :

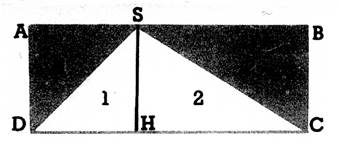
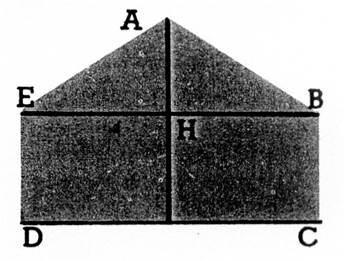
Examinons le triangle SCD il est la moitié du rectangle ABCD, car on trouve dans le rectangle ABCD deux fois les parties « 1 » et « 2 » qui constituent le triangle SCD .
			La base DC du triangle, c’est le grand côté du rectangle (la longueur); la hauteur SH qui correspond à cette base, c’est le petit côté (la largeur).
Surface du rectangle : longueur x largeur ou base x hauteur Surface du triangle : Surface du rectangle ou base x hauteur 2 2 La surface d’un triangle, c’est la moitié du produit d’une base par la hauteur correspondante, toutes les dimensions étant exprimées en unités de même ordre. Remarque; selon la commodité du calcul, on peut a) prendre la moitié du produit base x hauteur; b) multiplier la demi -base par la hauteur; c) multiplier la base par la demi - hauteur; quelque soit le cas « a » ou « b » ou « c » le résultat du calcul sera toujours le même.
TRAVAUX : EVALUATION
1. Copiez et complétez le tableau, relatif à des triangles
Base	12 cm	16 m		35 m	24 m	1,40 m
Hauteur	8 cm	12 m		48 m	19,6 m	75 cm
Surface	…………….	……………		…………..	…………..	……………
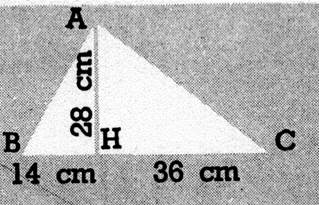
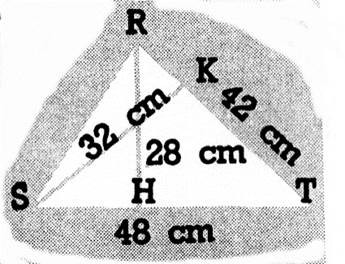
2. Calculez de deux façons la surface de chacun des triangles suivants R
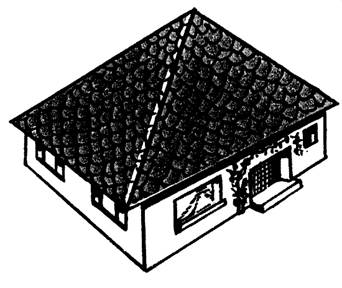
3. Le toit d’un pavillon est formé de 4 triangles égaux mesurant 8,6 m de base et 7,8 m de hauteur . Quelle est la surface totale du toit ? Une tuile coûte 0,45 € et il on faut 22 par mètre carré; combien coûtent les tuiles. de cette toiture ?
4. La figure ci dessous  représente le pignon d’une maison dans lequel
On donne les dimensions suivantes : DC = 9,2 m; BC = 3,25 m; AH = 2,8 m a) Quelle est la surface du pignon? b) Un maçon le couvre d’un crépi et demande 6,4 € par mètre carré. Quelle est la dépense?
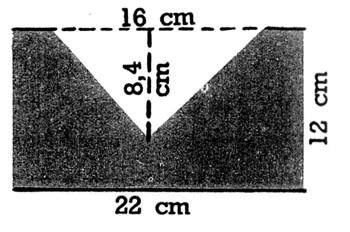
5 - Calculez la surface de chacune des figures ci-dessous, formées de triangles et de rectangles
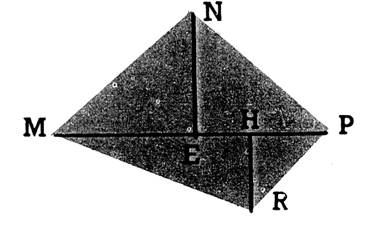
« A »				« B » on donne : MP = 14 cm ; NE = 6 cm ; RH = 4 cm