Pré requis:
|
|
|
|
|
|
|
|
ENVIRONNEMENT du
dossier:
AVANT :
|
APRES :
|
Complément
d’Info :
|
||
|
|
|
|
|
|
TITRE : LE
TRIANGLE QUELCONQUE (dit aussi : « triangle
scalène »)
|
|
|
|
|||
Travaux ; devoirs
|
|
Corrigé
|
|||
|
|
Contrôle |
évaluation |
|||
|
|
|
|
|
|
|
|
Interdisciplinarités : (matière concernée) |
||||||||
|
F |
H |
Géo. |
Vie quotidienne et vie familiale |
Autres : |
Sciences et technique |
Physique Chimie Electricité |
Statistique. |
|
COURS
TRAVAUX PRATIQUES :
|
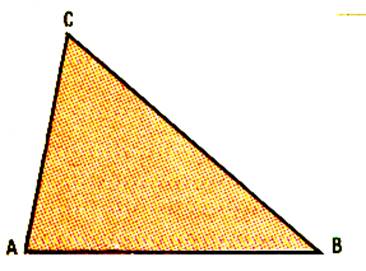
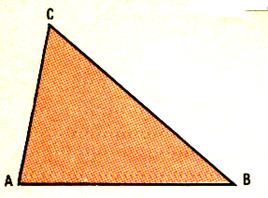
Sur une feuille blanche ; marquer 3 points A ; B ; C . Les joindre . Nous obtenons une figure à
trois côtés . Nous l’appelons « triangle » |
|
|
|
|
|
Découper le triangle précédent. Par pliage comparons les longueurs des côtés. Classer les longueurs des segments du plus grand au plus petit . [AC ] ;
[CB] ; [BA] : Puis les angles . Classer les angles du petit au plus grands. |
exemple :
[BA]> [CB] >[AC ] et
|
|
Classer les angles du petit au plus grands. |
|
Conclusion : si aucun
coté n’a la même longueur ; si
aucun angle n’a la même mesure , si il ne
possède pas un angle droit , le triangle
est un triangle quelconque .
*Le triangle quelconque a 3 côtés
inégaux et 3 angles inégaux .
Activité 2 :Somme des angles dans un triangle :
|
Découpons les angles 1 ;
2 ; 3 du triangle. |
|
|
Placer sur une même lignes et coller ces angles les uns à côté des autres . Quelle est la valeur de ces trois angles ? |
|
Activité 3 :
Identifier le ou les triangles quelconques suivants : ( entourer le numéro)
Pourquoi les autres ne sont pas quelconques ?
|
|
Activité 4 : CONSTRUIRE par
TRACE UN TRIANGLE QUELCONQUE
|
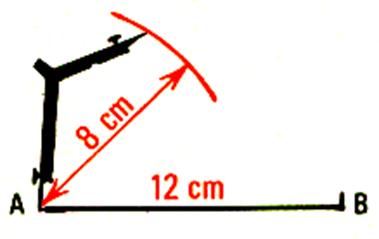
Exemple : tracer un triangle dont les côtés mesurent : AB =
12 cm ; AC = 8 cm ; BC = 10 cm |
|
|
1°) Tracer le segment de droite AB 2°) régler l’écartement du compas ( règle
graduée) à 8cm et tracé un arc de cercle |
|
|
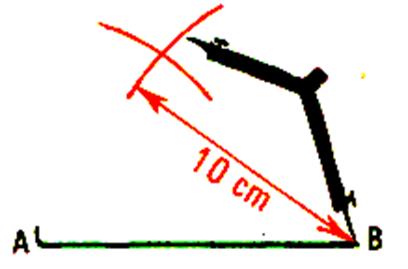
3°) régler l’écartement du compas ( règle
graduée) à 10 cm et tracé un arc de cercle. Celui croise l’arc tracé
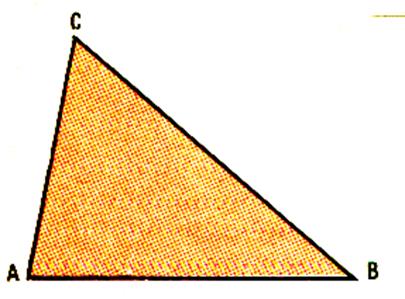
précédemment.( point C) 4°) Tracer AC et BC |
|
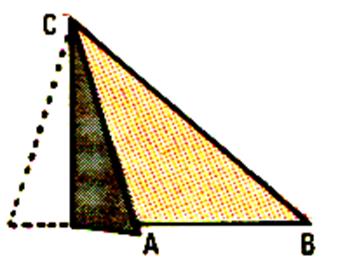
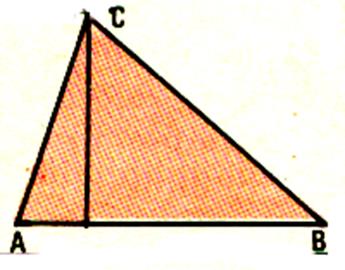
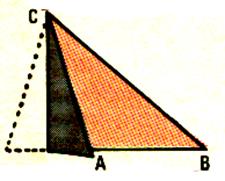
Activité 5 LES HAUTEURS
|
Prendre le triangle découpé précédemment . |
|
|
Plier le triangle comme le montre le croquis ( A et B sur la même ligne) ; |
|
|
Déplions ; traçons cette droite . Mesurer l’angle formé par le pli et le côté AB .
Que pouvons nous conclure ? L’angle est droite la droite est perpendiculaire .
On l’appelle « hauteur ». |
|
Activité complémentaires :
a) Par pliage
, menons les deux autres hauteurs du triangle .Que constatons
nous ?
Elles
se coupent en un même point.
b) Reproduire les triangles ci-dessous :
Pour chacun tracer les hauteurs .
|
|
c) Tracer un triangle ayant 7 cm de base et 4 cm de hauteur
. Pourrait – on eu dessiner d’autres ?
TRAVAUX AUTO FORMATIFS.
1°) Caractéristiques d’un triangle quelconque : ?
|
Sur une feuille blanche ; marquer 3 points
A ; B ; C . Les joindre . Nous
obtenons une figure à trois côtés . Comment
l’appelons – nous ? …………………… |
|
|
Découper le triangle précédent. Comparer les longueurs des côtés. Classer les longueurs des segments du plus grand
au plus petit .
[AC ] ;
[CB] ; [BA] : Puis les angles . Classer les angles du petit au plus grands. |
|
Activité 2 :Somme des
angles dans un triangle :
|
Découpons les angles 1 ; 2 ; 3 du triangle. |
|
|
Placer sur une même lignes et coller ces angles
les uns à côté des autres . Quelle est la valeur de ces trois angles ? |
|
Activité 3 :
Identifier le ou les triangles quelconques
suivants : ( entourer le numéro)
Pourquoi les autres ne sont pas quelconques ?
|
|
Activité 4 : CONSTRUIRE par TRACE UN TRIANGLE
QUELCONQUE
|
Tracer un triangle dont les côtés mesurent :
AB = 12 cm ; AC = 8 cm ; BC = 10 cm |
|
Activité
5 LES HAUTEURS
|
Prendre le triangle découpé précédemment
. |
|
|
Plier le triangle comme le montre le croquis ( A et B sur la même ligne) ; |
|
|
Déplions ; traçons cette droite
. Mesurer l’angle formé par le pli et le côté AB . Que pouvons nous conclure ? |
|
Activité complémentaires :
a) Par pliage , menons les deux autres hauteurs du triangle .Que
constatons nous ?
b) Reproduire les triangles ci-dessous :
Pour chacun tracer les hauteurs .
|
|
c) Tracer un triangle ayant 7 cm de base et 4 cm de
hauteur . Pourrait – on eu dessiner d’autres ?