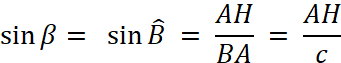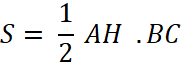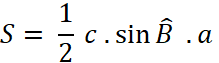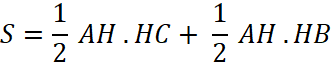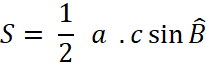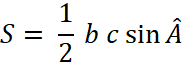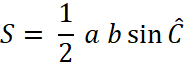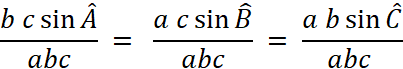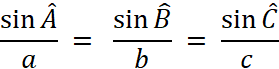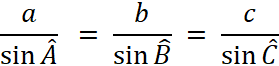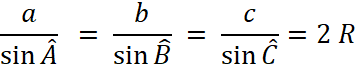Pré requis:					Doc revu en avril 2020.
Les triangles quelconques.
ENVIRONNEMENT du dossier:
Index warmaths			Objectif précédent : Relations métriques dans le triangle rectangle .				Objectif suivant 1°) Suite : relation trigonométrique dans le triangle quelconque…			Info Générales : Pythagore Géométrie. Les sinus.
DOSSIER : LES RELATIONS METRIQUES DANS LE TRIANGLE QUELCONQUE.
	Vous avez étudier l’objectif précédent ,nous allons élargir , compléter cette étude appliquée aux triangle quelconque…
	1. Relation de PYTHAGORE ( Les vecteurs et la relation de PYTHAGORE )
	2. Relation des trois sinus
	Aire du triangle : cas 1 et cas 2
	3. Proportionnalité des longueurs des côtés aux sinus des angles opposés
	4. Relation avec le rayon du cercle circonscrit .
TEST		COURS		Devoir Contrôle		Devoir évaluation		Interdisciplinarité Voir applications en arpentage .	Corrigé Contrôle		Corrigé évaluation
Ces relations trigonométriques dans le triangle quelconque vont permettre de calculer la longueur ou la valeur d’un angle

COURS
Relation de PYTHAGORE : généralisation
SOS rappels
1°) Les vecteurs et la relation de PYTHAGORE :
( Relation de Châles ) (info relation de Châles)
On transforme , on peut écrire ( en conservant l’égalité ) On élève les deux membres au « carré » on développe le deuxième membre ( et on regroupe les termes ) :
*lire « produit scalaire »
A propos de
…. On remplace dans l’égalité ci-dessus ; pour obtenir :
Aussi :
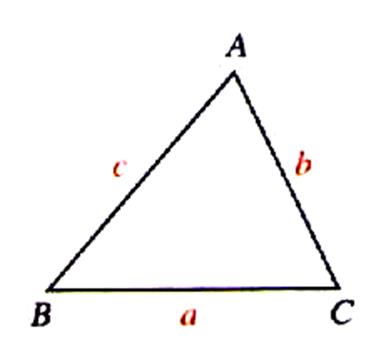
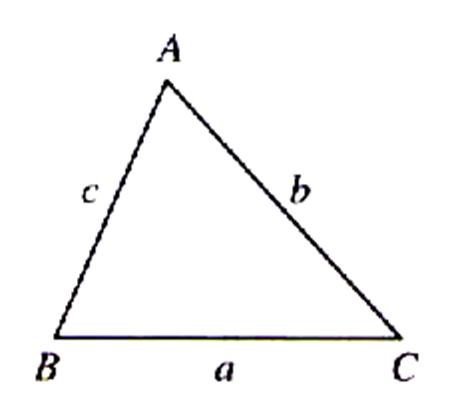
Si dans un triangle quelconque on désigne par « a » ; « b » ; « c » les longueurs des côtés opposés aux sommets A ; B ; C Par A ; B et C une mesure des angles  ; et du triangle , on obtient ( on écrit)  :
Par permutation circulaire nous obtenons les relations suivantes :
remarque : si l’angle est droit ( 90°) , le cosinus , on retrouve la relation de Pythagore du triangle rectangle
2°) Relation des trois sinus
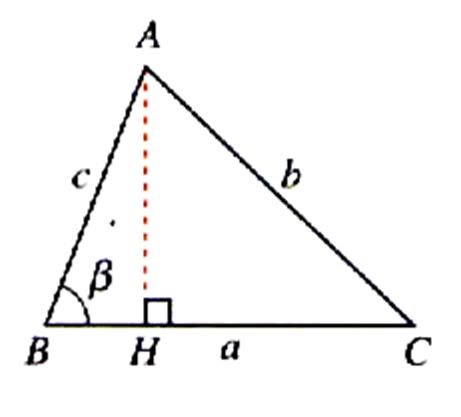
a) Calcul de l’ Aire du triangle : cas 1
soit « S » l’aire du triangle ABC. H est sur [BC] , donc - Dans le triangle rectangle On remarque que : et que Ce qui permet d’écrire que et Aussi dans le calcul de l’aire du triangle « S » devient : AH = c sin B et BC = a Ainsi en remplaçant dans  : devient l’égalité :
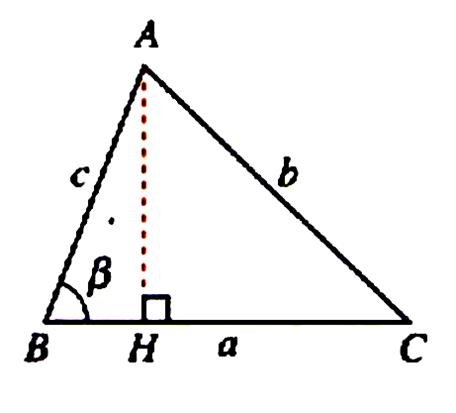
b) Aire du triangle : cas 2
Le point « H » est extérieur à [BC] , donc : L’aire du triangle ABC ( notée : S ) est égale à l’aire du triangle AHC plus l’aire du triangle AHB. Soit : Nota : D’ou Rappels sur « sinus d’un angle ». - On en déduit que la hauteur Ou alors : Et on sait aussi que  : : On peut aussi écrire que D’où le calcul suivant de « S » ( nous en déduisons que …)  : S est égale à la base par la hauteur divisées par 2 . En appliquant la démarche ci-dessus : De même nous pourrions trouver : ; et
3°) Proportionnalité des longueurs des côtés aux sinus des angles opposés
Ci-dessus nous avons montré que nous pouvions trouver « S » de 3 façons différentes.:
Aussi :
Après simplification , on en déduit que
en divisant les membres de ces égalités par le produit « abc » :nous obtenons la suite d’ égalité suivante :
Après simplification :
En conclusion on trouvera souvent l’égalité suivante :
5°) Relation avec le rayon du cercle circonscrit .
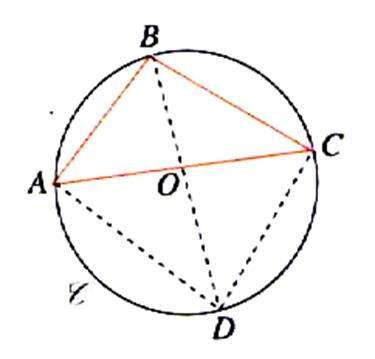
Soit le cercle circonscrit au triangle ABC .Nous désignons par « O » son centre et par « R » son rayon.
Nous plaçons sur la circonférence le point « D » diamétralement opposé au point « B » Les angles BAC et BDC intercepte la même corde sur le cercle . Ces angles sont égaux Ces angles sont supplémentaires Les angles BAC et BDC intercepte la même corde sur le cercle
Ces angles sont supplémentaires Les angles BAC et BDC intercepte la même corde sur le cercle
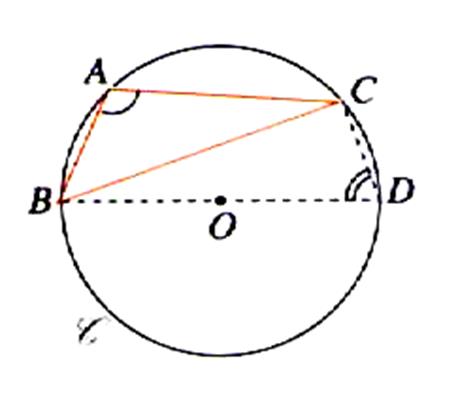
Dans les deux cas le sinus de l’angle BDC ( à noter : ) est égal au sinus le l’angle BAC ( à noter : ) qui est égal au sinus de l’angle A ;( à noter : ) Le triangle BDC est rectangle en C , alors  : En conclusion :
Ce chapitre fait souvent l’objet d’un devoir pour aider à montrer qu’un triangle est rectangle , que le point « O » est le milieu de l’ hypoténuse .