|
DOSSIER : LES RELATIONS
entre les éléments d’un TRIANGLE
QUELCONQUE. |
|
||||||||||
|
|||||||||||
|
Citer les 3 relations que l’on utilise pour
résoudre les triangles quelconques en trigonométrie |
|
||||||||||
|
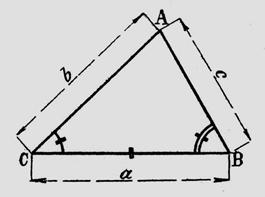
Relation 1 : Règle des sinus :
|
|
||||||||||
|
Relation
2 : a = c cos |
|
||||||||||
|
Relation 3 : a² = b² + c² - 2 c b cos |
|
||||||||||
|
|
|
||||||||||
|
|||||||||||
|
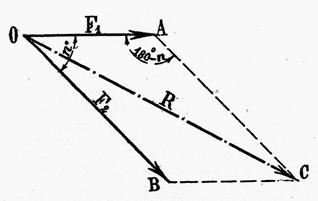
Application : On donne
deux forces : si F1
= 15 N
F 2 = 25 N et L’angle 1°) Calculer la valeur de la résultante 2°) Donner la valeur de la direction de la
résultante |
|||||||||||
|
|
On
peut établir la relation : R² =
F1² + F 2²
- 2 F1 ´ F 2 ( - cos Exemple : On trouvera :
R² = 1380,25
R = 37 ,15 N
|
||||||||||
|
a) Valeur de la résultante : On considère par exemple Le triangle OAC : On établit la relation
suivante , à partir de ce que nous avons vu précédemment :
En remplaçant les segments précédents
par leurs valeurs respectives et en remarquant que cos A = - cos O ( angles supplémentaires) , on a
finalement : R² = F1²
+ F 2² - 2 F1
´ F 2 ( - cos R² = F1² + F 2² +
2 F1 ´ F 2 ´ cos Si par exemple : si F1² = 15 N
F 2 = 25 N et L’angle (d ‘après la table : cos 45° =0,707) , on remplace dans (1)
On aura : R² = 15 ² + 25 ²
+ 2 ´ 15 ´ 25 ´ 0 ,707 R² =
225 + 625 +
750 ´
0 ,707 R² = 850
+ 750 ´ 0 ,707 On trouvera : R²
= 1380,25
On fait ensuite la racine carrée
de R² :
R = 37 ,15 N |
|||||||||||
|
b)
Direction de la
résultante : La relation du sinus permet d’autre part de calculer
l’inclinaison de la résultante par rapport à l’une quelconque des forces. Le triangle OAC donne
en effet : Ou En remplaçant par les valeurs données ou
calculées : et d’établir l’égalité
suivante :
D ‘après la table (ou la
calculatrice) :
on trouvera que le sinus de l’angle AOC = 28°20’ nota : En appliquant la
vérification sur la somme des angles d’un triangle , on constatera que l’angle obtus
supplément de l’angle AOC ne convient pas . |
|||||||||||
|
L’exemple précédent est un exemple de
résolution d’un triangle quelconque connaissant deux côtés et l’angle compris
. Les différents cas de résolution qui peuvent se présenter dans la pratique sont traités
dans les pages suivantes. |
|||||||||||
|
Faire Les
4 EXERCICES types :
|
|||||||||||
|
|
|||||||||||
|
Résoudre un triangle quelconque dont on connaît un
côté « a » et les deux angles adjacents
|
|||||||||||
|
Les données sont : « a » = 83,25 m
|
Les inconnues sont donc : « b » , « c » , et l’angle A. |
|
|||||||||
|
Formules de résolution. A = 180° - ( |
|||||||||||
|
|
|||||||||||
|
on en tire |
|||||||||||
|
|
|||||||||||
|
Calcul de l’angle |
|||||||||||
|
|
|
|
|||||||||
|
Calcul de « b » : Sin 58° 20’ =
0,851 ; sinus 82° 10’= 0,991
|
|||||||||||
|
Calcul de « c » : Sin 39° 30’ = 0,636
; sinus 82° 10’=
0,991
|
|||||||||||
|
Résoudre un triangle quelconque dont on connaît
deux côtés « b » et
« c » et l’angle
|
|||||||||||
|
Les données sont : « b » = 160,60 m « c » = 112 , 90 m |
Les inconnues sont donc : « a » =
? |
|
|||||||||
|
Formules de résolution. |
|||||||||||
|
a²
= b² + c² - 2 c b cos |
|||||||||||
|
|
|||||||||||
|
Dont on tire |
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
Calcul de
« a » :
( cos 26° 15 ‘ = 0,897)
a² = ( 160,60 ) ² + ( 112,90)² - 2 ´ 160,60 ´ 112,90 ´ cos 26° 15’
a² = ( 160,60 ) ² + ( 112,90)² - 2 ´ 160,60 ´ 112,90 ´ 0,897
a² = 38538,77 -
32 528,34 = 6010,43
« a » = 77,50 m
|
|||||||||||
|
Calcul de sinus de
l’angle B pour en déduire l’angle B |
|||||||||||
|
Sin
26° 15’ = 0,442
sin
On trouve |
|||||||||||
|
Calcul de sinus de
l’angle |
|||||||||||
|
sin |
|||||||||||
|
On vérifiera que « Les valeurs de |
|||||||||||
|
Résoudre un triangle quelconque dont on
connaît les trois côtés « a » , « b » et
« c » .
|
|||||||||||
|
Les données sont : « b » = 118 m « c » = 65 ,90 m « a »
= 80,55 m |
Les inconnues sont donc : |
|
|||||||||
|
Formules de résolution : |
|
||||||||||
|
a² = b² + c² - 2 c b cos de cette formule on tire : 2 c b cos et
|
|
||||||||||
|
par la relation des sinus : |
|
||||||||||
|
par transformation , on trouvera : |
|
||||||||||
|
|
|
||||||||||
|
Calculs : |
|
||||||||||
|
Calcul de l’angle
pour 0,291 sur
la table on lit :
73° 5’ et pour - 0,291 : l’angle
L’angle pour le calcul de |
|
||||||||||
|
Calcul de
l’ angle
|
|
||||||||||
|
|
|
||||||||||
|
Pour 0,534 l’ angle
|
|
||||||||||
|
Calcul de
l’ angle On utilise la formule |
|
||||||||||
|
|
|
||||||||||
|
D ‘ après la calculatrice
pour 0,653 on trouve l’angle C
= 40 ° 45’ Nota : les
suppléments des angles B et C ne conviennent pas . (voir vérification
avec la somme des angles dans un
triangle) |
|
||||||||||
|
Quatrième cas : (deux exemples seront
proposés : le premier débouche sur un ensemble de solutions . Le second
exemple débouche sur deux ensembles de
solutions possibles) |
|
||||||||||
|
Résoudre un triangle quelconque dont on connaît
deux côtés et l’angle opposé à l’un
d’eux. |
|
||||||||||
|
Les données : « a » « b » l’angle A. |
Les inconnues sont : L’angle B ; L’angle C « c » |
|
|
||||||||
|
Les formules de résolution sont : |
|
||||||||||
|
|
|
||||||||||
|
( la valeur en degré de l’angle B s’obtient au moyen de la calculatrice ou
d’une table.) |
|
||||||||||
|
Puis l’angle |
|
||||||||||
|
Et |
|
||||||||||
|
Exemple premier : un seul
ensemble de solutions : |
|
||||||||||
|
Exemple numérique : « a » =
95,75m « b » = 70,40 m
|
|
||||||||||
|
|
|
||||||||||
|
Calcul de l’angle |
|
||||||||||
|
d’après la calculatrice : à 0,560
correspond l’angle |
|
||||||||||
|
|
|
||||||||||
|
Calcul de l’angle |
|
||||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
Calcul de « c » : |
|
||||||||||
|
Sin 96° 17’
= sin ( 180° -
96° 17’) = sin 83° 43’ (@
info. +) Et
sin 83° 43’ = 0,994 |
|
||||||||||
|
le côté c = 124,90 m |
|
||||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
Pour sinus B = 0,560 une deuxième valeur de B est 180° - 34° 3’
= 145° 57’. (@ info+) |
|
||||||||||
|
Mais
alors Avec les
données suivantes on peut voir que deux solutions sont
acceptables. |
|
||||||||||
|
Exemple second : on peut proposer deux ensembles
de solutions : |
|
||||||||||
|
|
|
||||||||||
|
On donne : « a » = 77,95 m ;
« b » = 98,10 m et l’angle A = 42°55’ |
|
||||||||||
|
|
|
||||||||||
|
Calcul de l’angle |
|
||||||||||
|
Pour calculer l’angle |
|
||||||||||
|
pour
0,851 , on
a ou |
|
||||||||||
|
Calcul de l’angle |
|
||||||||||
|
2 cas |
|
||||||||||
|
1°)
|
|
||||||||||
|
|
|
||||||||||
|
2°) |
|
||||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
On trouve 2 valeurs pour l’angle B et pour l’angle Vérifications : Cas 1 : 42° 55’ + 59 ° + 78°5’ =
180° Cas 2 : 42° 55’ +
121° + 16° 5’ = 180° |
|
||||||||||
|
Calcul de la longueur de « c » |
|
||||||||||
|
Cas1 : Soit
« c » = 112,06 m |
|
||||||||||
|
Ou
deuxième solution : |
|
||||||||||
|
Cas 2 |
|
||||||||||
|
Soit
« c » = 31,70 m |
|
||||||||||
|
|
|
||||||||||
|
SERIE D’ EXERCICES
sans corrigé : |
|
||||||||||
|
|
|
||||||||||
|
I )
Résoudre un triangle quelconque connaissant : |
|
||||||||||
|
Triangle 1 |
|
||||||||||
|
« a » =
728,5 m |
« b » = ? |
« c » = ? |
|
||||||||
|
|
|
|
|
||||||||
|
|
|
||||||||||
|
Triangle 2 |
|
||||||||||
|
« a » =
164 , 30 m |
« b » = ? |
« c » = ? |
|
||||||||
|
|
|
|
|
||||||||
|
Triangle 3 |
|
||||||||||
|
« a » = |
« b » =632 , 8 m |
« c » =
340 , 5 m |
|
||||||||
|
|
|
|
|
||||||||
|
Triangle 4 |
|
||||||||||
|
« a » = |
« b » = 416,10 m |
« c » =
802, 4 m |
|
||||||||
|
|
|
|
|
||||||||
|
Triangle 5 |
|
||||||||||
|
« a » = 153,20 m |
« b » = 90 , 50 m |
« c » = 162,30 m |
|
||||||||
|
|
|
|
|
||||||||
|
Triangle 6 |
|
||||||||||
|
« a » = 146,15 m |
« b » = 162, 25 m |
« c » = 180, 75 m |
|
||||||||
|
|
|
|
|
||||||||
|
Triangle 7 |
|
||||||||||
|
« a » =
124,75 m |
« b » =
156,25 m |
« c » =
|
|
||||||||
|
|
|
|
|
||||||||
|
Triangle 8 |
|
||||||||||
|
« a » =
219,65 m |
« b » = 184, 45 m |
« c » = |
|
||||||||
|
|
|
|
|
||||||||
|
|
|
||||||||||
|
|
|
||||||||||
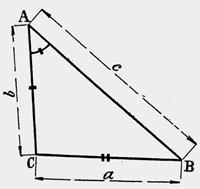
|
Calculer la hauteur AH d’un triangle ABC dans lequel on a : « a » = 4,25 m ; |
|
||||||||||
|
|
|
||||||||||
|
Résoudre un triangle ABC inscrit dans une
circonférence de rayon donné « R » = 0,125 m , sachant que les
angles |
|
||||||||||
|
|
|
||||||||||
|
On donne un triangle ABC ; « a » = 2,75 m ; calculer 1°)le rayon
« r » du cercle inscrit ; 2°) le rayon ra exinscrit dans l’angle |
|
||||||||||
|
|
|
||||||||||
|
INTERDISCIPLINARITE : mécanique. |
|
||||||||||
|
1°) Un corps est soumis à l’action de deux forces concourantes ,,
l’une de 1650 N l’autre de 3250 N .
Ces forces font entre elles un
angle de 56° 25’ . Calculer la
valeur de la résultante des
deux forces ainsi que son inclinaison par rapport aux deux composantes. |
|
||||||||||
|
|
|
||||||||||
|
2° ) On
veut remplacer l’action d’une force de 900 N
par celles de deux forces ayant même point d’application que la
première . |
|
||||||||||
|
|
|
||||||||||
|
|
|
||||||||||