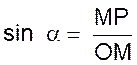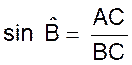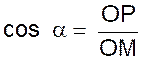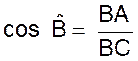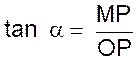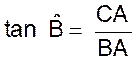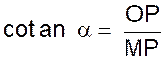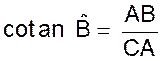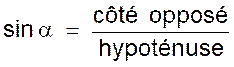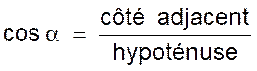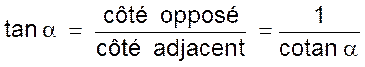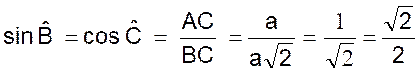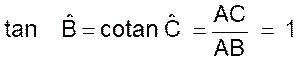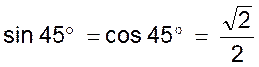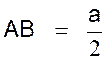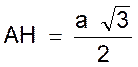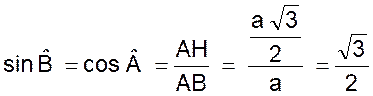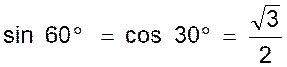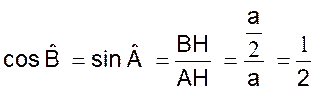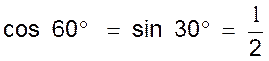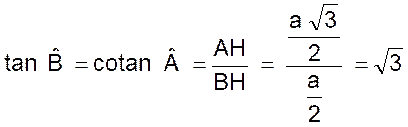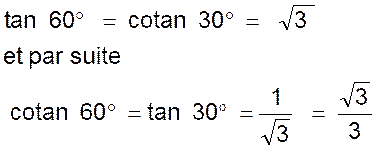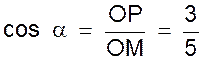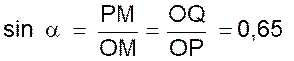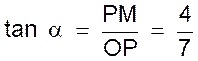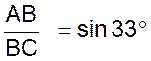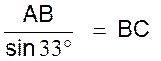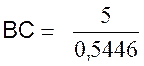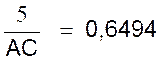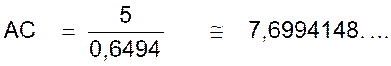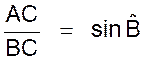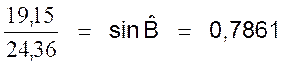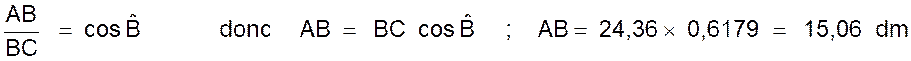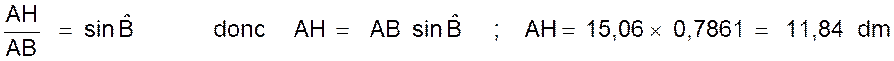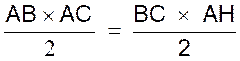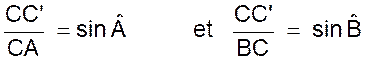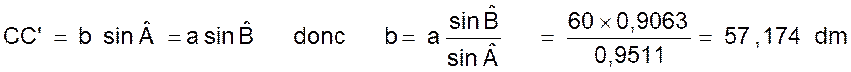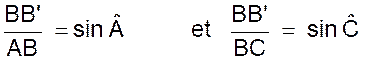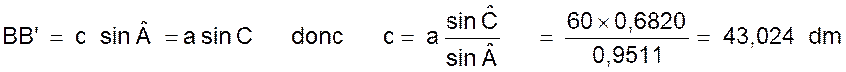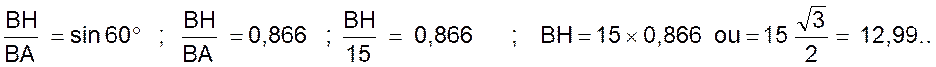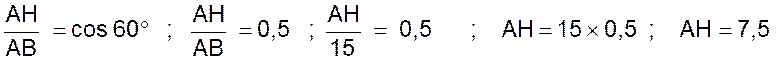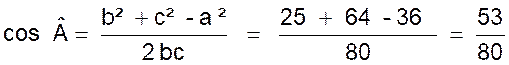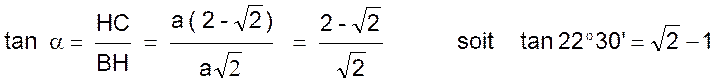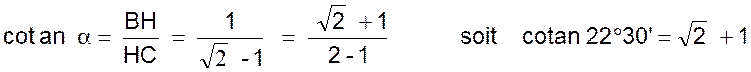Relations trigonométriques dans le triangle rectangle.

les relations que l’on peut établir entre les mesures « a » , « b » , et « c » des côtés d’un triangle ABC et les rapports trigonométriques des angles A , B et C de ce triangle sont appelées « relations trigonométriques » dans le triangle ABC

2°) Théorème

Dans tout triangle rectangle , un côté de l’angle droit est égal :

1°) au produit de l’hypoténuse par le sinus de l’angle opposé à ce côté ou par le cosinus de l’angle adjacent à ce côté.

2°) Au produit du second côté de l’angle droit par la tangente de l’angle opposé à ce côté ou par la cotangente de l’angle adjacent à ce côté.

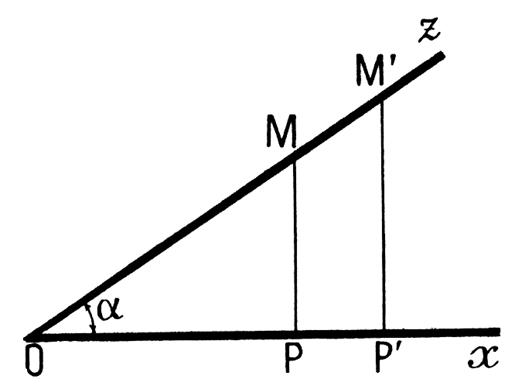
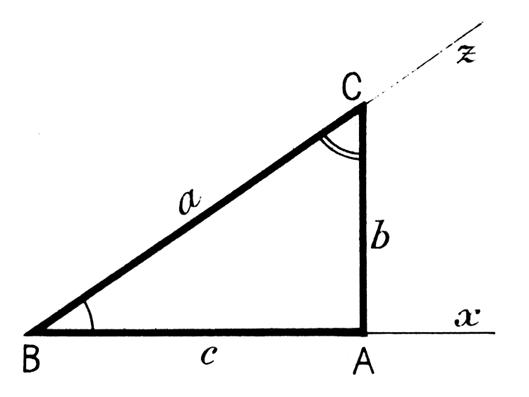
Ce qui se montre , en comparant avec ce qui a été vu dans le cours sur les rapports trigonométriques:

: Soit le triangle ABC , rectangle en A.

On a remplacé OP par BA et BC par OM , nous pouvons établir un parallèle

Soit

AC = BC sin ; AB = BC cos ; AC = AB tan ; AB = AC cotan

Donc :

b = a sin ; c = a cos ; b = c tan ; c = b cotan

en nous situant en l’angle C ; on peut établir les relations suivantes :

c = a sin ; b = a cos ; c = b tan ; b = c cotan

Soit finalement

b = a sin = a cos

c = a sin = a cos

b = c tan = c cotan

c = b tan = b cotan

Remarques :

a) le théorème précédent permet de retrouver les définitions ? on voit ainsi que dans un triangle rectangle dont un des angles aigus est égal à a ( l’autre b ) avec :

a° + b° = 90°

b) D’autre part la comparaison des formules précédentes permet de retrouver le théorème relatif aux angles complémentaires , car on en déduit :

sin a = cos b et tan a = cotan b

3°) Rapport trigonométrique des angles de 45° ; 30° et 60° ( @ info complément)

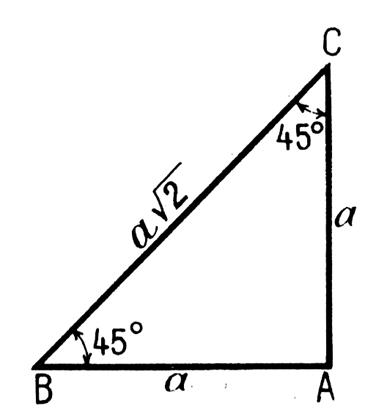
a) Soit un triangle rectangle isocèle ABC : ( @info ++)

AB = AC = a et en A nous avons un angle droit.

Nous sommes en présence d’un demi carré ou BC est une diagonale.

L’angle B = l’angle C = 45° et BC =

Par suite :

Donc

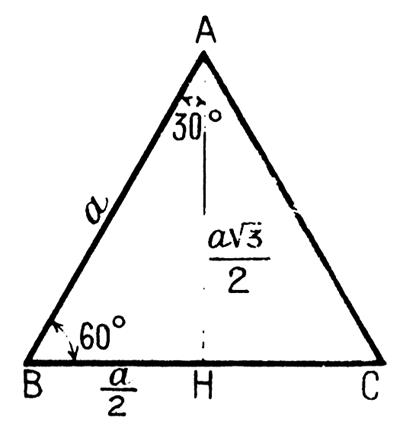
2°) Soit le triangle équilatéral BAC ( @ info + )

La droite i« AH » est à la fois la médiane bissectrice , médiatrice , hauteur .Elle coupe l’angle A en deux parties égales .

Soit le triangle ABH :

L’angle B = 60° ; l’angle A = 30° , l’angle en H = 90° ,

Donc

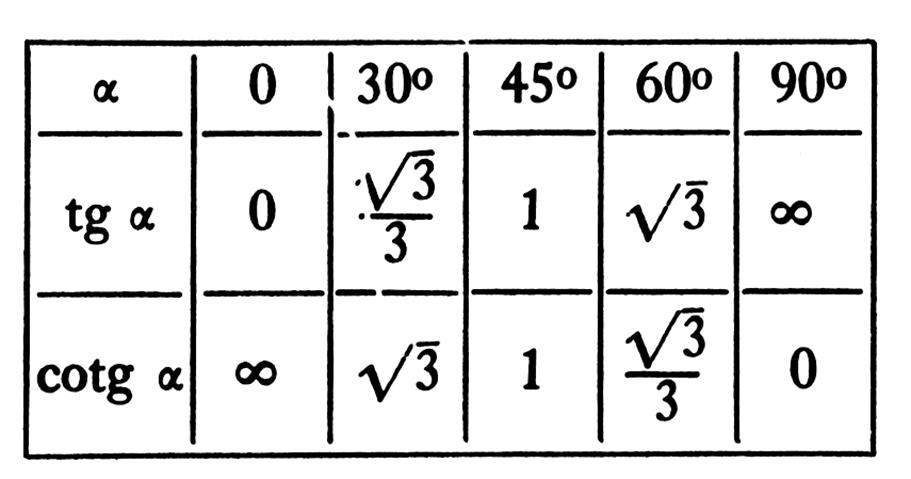
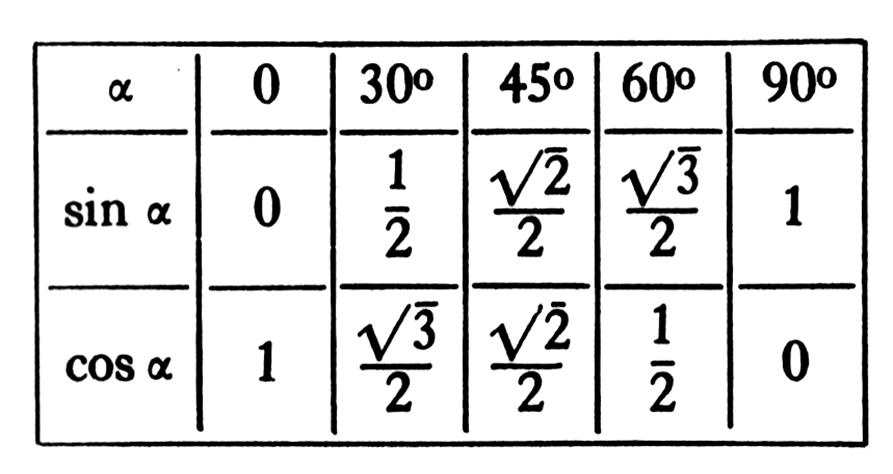
On peut dons dresser le tableau : ( @ info ++ : « angles remarquables » +)

45a

45b

Il est très utile de savoir ces valeurs ou de pouvoir les retrouver rapidement.

4°) Construire un angle connaissant un de ses rapports trigonométriques : (@info plus)

On est ramené à construire un triangle rectangle OPM connaissant le rapport de deux de ses côtés.

a) Construire l’angle dont le cosinus est ( 3/5) . (figure ci dessous)

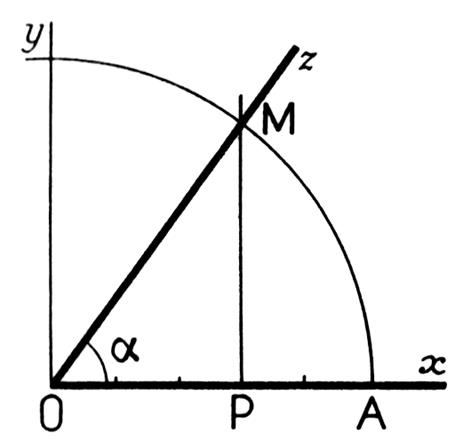
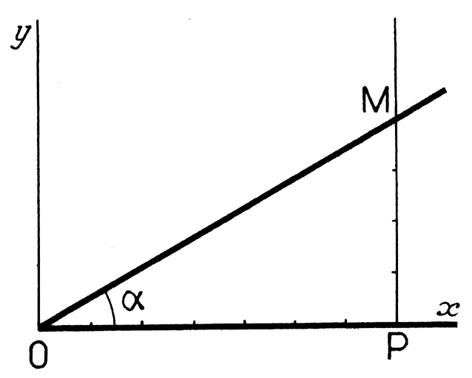
Procédure :

Porter sur une demi- droite Ox deux segments OP = 3 unités et OA = 5 unités.

Tracer une perpendiculaire en P

Tracer le cercle de centre O et de rayon OA .

Le cercle coupe la perpendiculaire de « P » en M .

L’angle a est tel que :

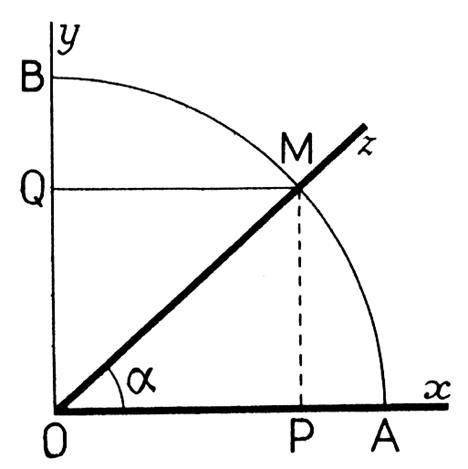
b) Construire l’angle aigu dont le sinus est 0,65 . ( figure ci dessous)

Procédure :

- Tracer deux demi droites perpendiculaires Ox et Oy .

- Tracer un cercle de centre O , de rayon = a = 100 mm. (par exemple)

On obtient OB = OA = a .

- Tracer OQ = 0,65 fois a = ( 0,65 fois 100)

Soit OQ = 65 mm

- tracer la parallèle à Ox , elle coupe le cercle en M .

- tracer OM

Le cercle de centre O passant par A coupe , du côté de Ox , la perpendiculaire en Q à Oy en M .

L’angle xOM = a est tel que

c) Construire l’angle dont la tangente est égale au rapport (4/7) . (voir figure ci dessous)

Tracer deux demi- droites perpendiculaires Oy et Ox .

Porter sur Ox le segment OP = 7 unités

Tracer une perpendiculaire en « P ».

Tracer sur la perpendiculaire à Ox en P , un point tel que PM = 4 unités.

Tracer OM .

L’angle a est donné par l’angle MOx

Est tel que :

Ainsi , après ces trois exemples types : si l’on connaît la mesure d’un angle aigu , on peut donc à l’ aide de la table déterminer sa tangente et construire cet angle sans rapporteur

5°) Résolution d’un triangle rectangle. ( @info ++notion+) et ( @résoudre)

Si dans un triangle rectangle on connaît deux éléments, dont une longueur au moins , on peut calculer les éléments inconnus.

Cette opération est appelée « résolution du triangle »

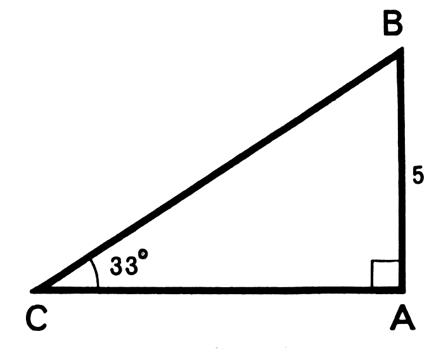
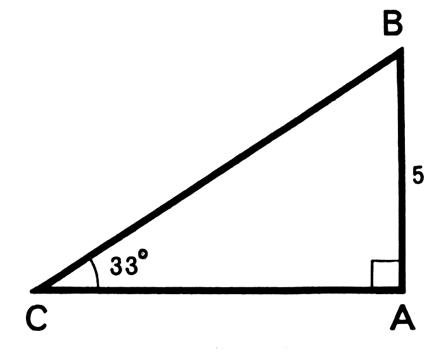
Exemple 1 :

Dans un triangle ABC , rectangle en A , on donne AB = 5 cm et l’angle C. = 33° .

Calculer BC et CA

Résolution : On recherche sur la table :Sin 33° = 0, 5446 ;Cos 33° = 0,8387 ;Tan 33° = ……….

a) Calcul de BC :

On sait que AB = 5 et que

on en déduit que AB = BC sin 33° ,et que

donc ; = 9,18 10 503 soit BC = 9,18 cm

b) Calcul de CA :

(Remarque : pour calculer CA , on prend comme point de départ AB = 5 cm , on ne passe pas par Pythagore)

On sait que : soit

On transforme : soit AC = 7,70 cm

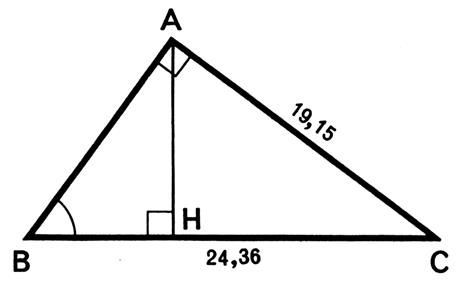
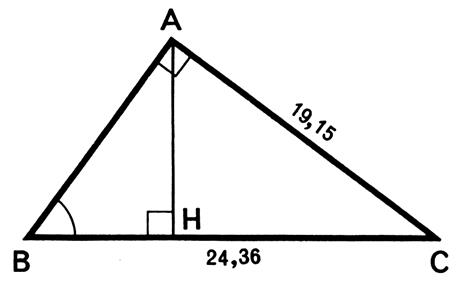
Exemple 2 :

Calculer les angles B et C , le côté AB et la hauteur AH du triangle ABC rectangle en A sachant que BC = 24, 36 dm et AC = 19,15 dm .

a) Calcul du sinus de l’angle B :

On sait que : soit (valeur arrondie )

En degré : D’après la calculatrice l’angle B = 51 , 82253 ° ou 52° 41’ 10’’ ( voir sur la table) , on trouve pour l’angle C = 90° - 52,82253 ° = 38,17747 ° ( = 38° 18’ 50’’ )

En grade : on trouve : l’angle B = 57,59 gr et l’angle C = 42,41 gr

b) Calcul de AB :

c) Calcul de AH :

Remarque : On connaît la valeur de AB ; nous nous plaçons dans le triangle rectangle BAH.

Nota : Nous verrons dans une autre leçon que l’on peut trouver la valeur de AH en passant par du triangle .en posant l’égalité suivante :

6°) Résolution d’un triangle quelconque . ( scalène) ( @ info +++)

En menant l’une des hauteurs du triangle ABC , on détermine deux triangles rectangles dans lesquels on peut appliquer les relations suivantes:

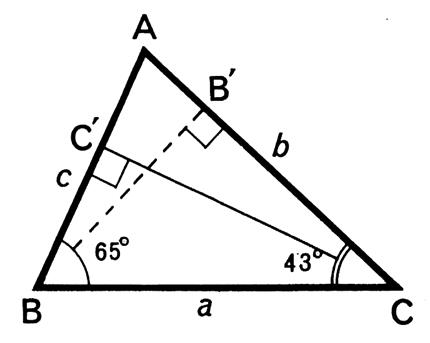
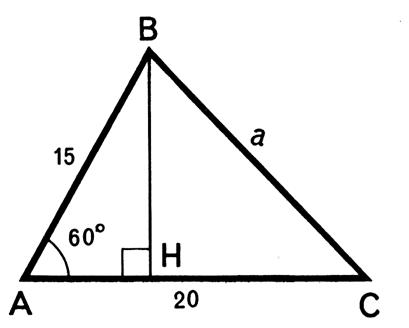
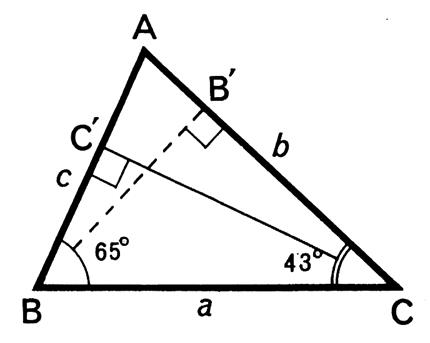
Exemple 1 :

Dans le triangle ABC on donne : BC = a = 60 cm et les angles : angle B = 65° et l’angle C = 43° .

Calculer AC = b et AB = c

(Voir figure ci -contre ).

Dans la table ou la calculatrice on relèvera les valeurs des rapports trigonométriques :

Dont les Sin B = 0,9063 ; sinus A = 0,9511 et sinus C = 0,6820

a) Calcul de l’angle A :

on sait que la somme des angles : A + B + C = 180°

donc l’angle A = 180° - ( 65° + 43 ° ) soit l’angle A = 72°

b) calcul de « b » ( CA)

Menons la hauteur CC’ :

Dans les triangles rectangles ACC’ et BCC’ on obtient :

on en déduit que :

donc : b = 57,174 dm

c) calcul de AB :

Menons la hauteur BB’ :

Dans les triangles rectangles ACC’ et BCC’ on obtient :

on en déduit que :

donc c = 43,024 dm.

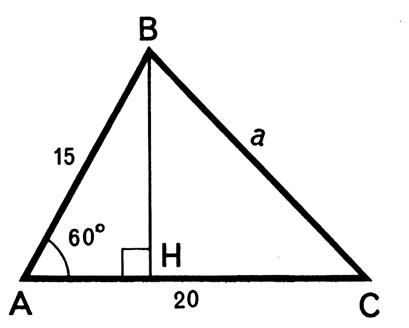
Exemple 2 :

Calculer la longueur du côté BC du triangle ABC sachant que AB = 15 m , AC = 20 m et l’angle A = 60°

( figure ci contre )

nota : nous savons que sin 60° = ou 0,8666….

Résolution :

a) Calcul de BH :

Menons par B la hauteur BH . Dans le triangle ABH rectangle en H :

on peut aussi écrire que BH = (7,5 )

b) Calcul de AH

c) calcul de CH (pour appliquer « Pythagore » dans le triangle BHC)

CH = 20 - 7,5 = 12,5

d) Calcul de BC.

(BC)² = ( BH)² + (HC)² ; ( BC)² = (7,5 )² + ( 12,5)² ; (BC)² = 325

BC = = 18,028 m

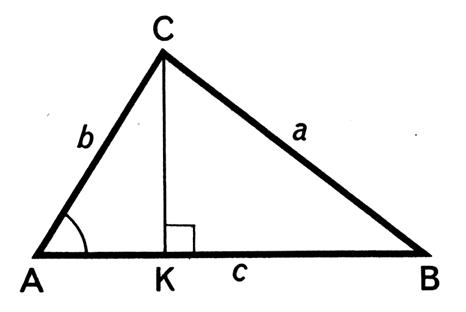
Exemple 3 :

Calculer l’angle A du triangle ABC sachant que

BC = a = 6

AC = b = 5

AB = c = 8

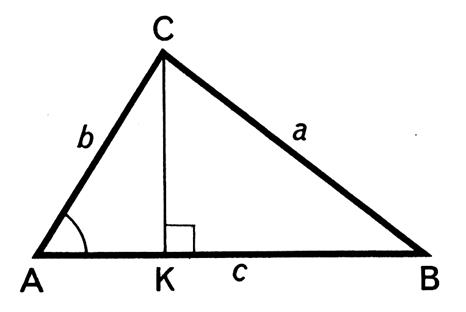
Résolution : Nous menons par « C » la hauteur CK .

On obtient CK = b sin et AK = b cos

D’où K B = AB - AK soit KB = c - b cos

Nous savons que ( BC) ² = (KB)² + ( KC)²

Nous remplaçons : a² = (c - b cos ) ² + (b sin )²

( à faire sur feuille )

D’où après développement : a² = b ² + c ² - 2 bc cos

Soit : cos = 0,6625 d’où d’après la table = 48 ° 30 ‘

D’après la calculatrice : 48,509183° ou 48° 30’ 33’’

7°) EXERCICE « type » résolu :

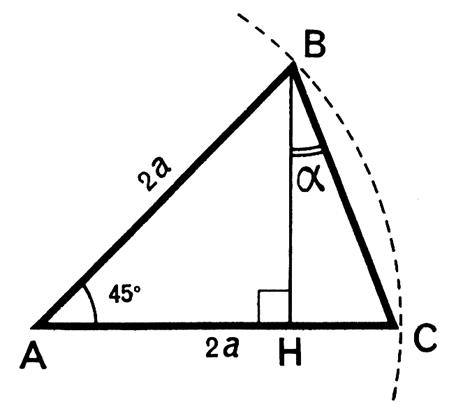
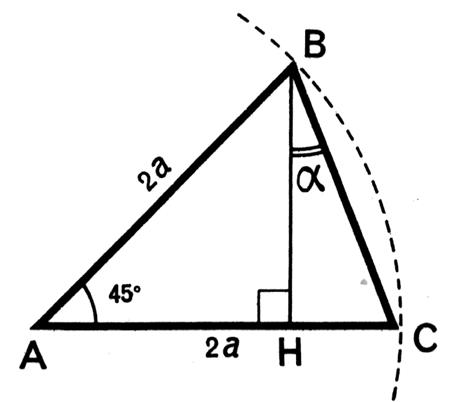
Dans un triangle isocèle ABC on donne AB = AC = 2a et l’angle = 45°.

On mène par « B » la hauteur BH .

On demande : Calculer les segments BH et HC et en déduire :

tan 22° 30’ et cotan 22°30’

Résolution :

Le triangle ABH est rectangle isocèle et AH = BH = 2 a sin 45° = a

D’où :

HC = 2a - a = a ( 2 - ) ;

Dans le triangle ABC on a l’angle B = l’angle c = ( 180° - 45°) / 2 .

D’où l’angle B = l’angle C = 67°30’

Et a = l’angle HBC = 22° 30’ .

Dans le triangle rectangle BHC :


Travaux autoformatifs.

CONTROLE :
1°)Citer les 4 rapports trigonométriques. 2°) Dessiner un triangle rectangle nommer les sommets et établir tous les rapports.
EVALUATION :

1°) Donner avec la table et la calculatrice les rapports trigonométriques des angles suivants :
25° =	31°=	43°=
57°=	81°=	83°=

2°) Déterminer l’angle aigu « x » tel que :
Sin x = 0,48	Cos x = 0,1550	Tan x = 0,3
Sin x = 0,84	Cos x = 0,9515	Tan x = 1,5




3°) Soit un angle aigu xOy tel que sin xOy = 3/5 a) sans se servir de la table, calculer cos xOy et tan xOy b) construire géométriquement cet angle .

Voir les exercices : ci @ info
Les travaux ci dessous sont corrigés dans le cours ?
4°) Construire un angle connaissant un de ses rapports trigonométriques : (@info plus)

a) Construire l’angle dont le cosinus est ( 3/5) .
b) Construire l’angle aigu dont le sinus est 0,65 .
c) Construire l’angle dont la tangente est égale au rapport (4/7) . (voir figure ci dessous)
5°) Résolution d’un triangle rectangle. ( @info ++notion+) et ( @résoudre)

PB 1 : Dans un triangle ABC , rectangle en A , on donne AB = 5 cm et l’angle C. = 33° . Calculer BC et CA

PB2 : Calculer les angles B et C , le côté AB et la hauteur AH du triangle ABC rectangle en A sachant que BC = 24, 36 dm et AC = 19,15 dm .

6°) Résolution d’un triangle quelconque . ( scalène)
PB 3 : Dans le triangle ABC on donne : BC = a = 60 cm et les angles : angle B = 65° et l’angle C = 43° . Calculer AC = b et AB = c (Voir figure ci -contre ). Dans la table ou la calculatrice on relèvera les valeurs des rapports trigonométriques : Dont les Sin B = 0,9063 ; sinus A = 0,9511 et sinus C = 0,6820

PB 4 : Calculer la longueur du côté BC du triangle ABC sachant que AB = 15 m , AC = 20 m et l’angle A = 60° ( figure ci contre ) nota : nous savons que sin 60° = ou 0,8666….

PB 5: Calculer l’angle A du triangle ABC sachant que BC = a = 6 AC = b = 5 AB = c = 8

PB 6: Dans un triangle isocèle ABC on donne AB = AC = 2a et l’angle = 45°. On mène par « B » la hauteur BH . On demande : Calculer les segments BH et HC et en déduire : tan 22° 30’ et cotan 22°30’