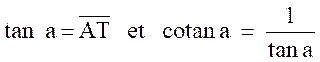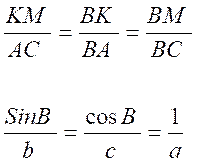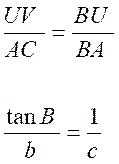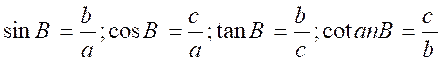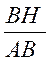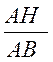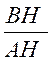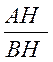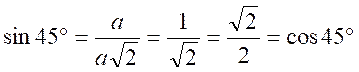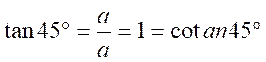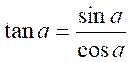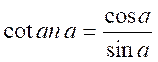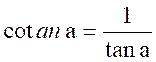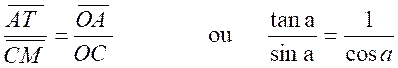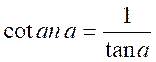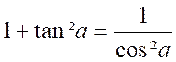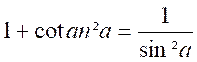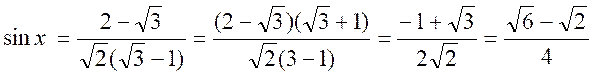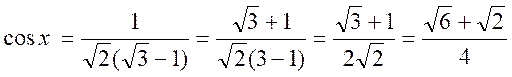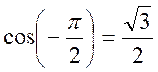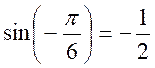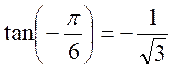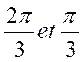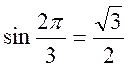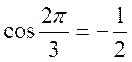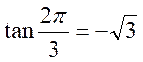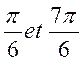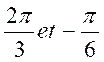Pré requis:
|
|
|
|
|
|
|
|||
|
|
|
||
|
|
|||
|
|
|
||
|
|
|||
|
|
|||
ENVIRONNEMENT du dossier:
|
Index warmaths |
Objectif précédent : |
Objectif suivant : |
Retour à la liste des objectifs
de formation A savoir : les
abréviations : « tg » et
« tan » , abréviations : lire « tangente » « cotg » et
« cotan » ,
abréviations :
lire « cotangente » |
|
|
|
|
|
DOSSIER
:: LES FONCTIONS
CIRCULAIRES.
Chapitre 1 : Définition de sin a ;
cos a ; tan a ; cotan a :
1-1 ) Le cercle trigonométrique (rappel)
1-2 ) sinus –cosinus d’un arc.
Périodicité.
1-3) Tangente et cotangente d’un arc
Chapitre 2 Fonction y = sin x et y = cos x :
Chapitre 3 Fonction y = tan x et y = cotan x :
Chapitre 4 Fonctions circulaires d’un angle trigonométrique :
Chapitre 5 Applications géométriques :
5-1
Application au triangle rectangle. Et le théorème
5-2
Application au triangle quelconque.
5-3
Fonctions circulaires des arcs. : 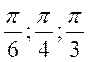
5-4
Tableau récapitulatif.
Chapitre 6 :
RELATIONS ENTRE
LES FONCTIONS CIRCULAIRES D’UN MEME ARC.
Chapitre
7 : ARC ASSOCIES ; LEURS EXTREMITES ; LEURS
FONCTIONS CIRCULAIRES.
|
TEST |
|
COURS
Chapitre 1 :
DEFINITION de « sin. a » ;
« cos. a », « tan. a »
et « cotan. a »
|
|
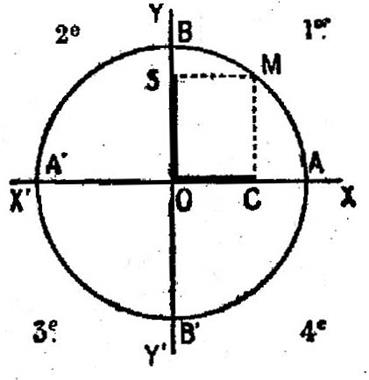
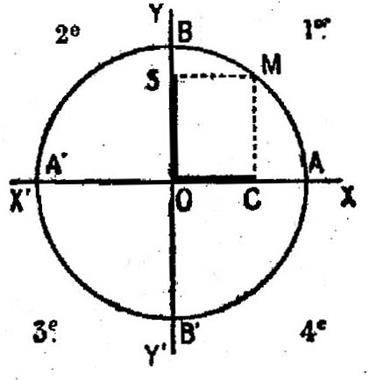
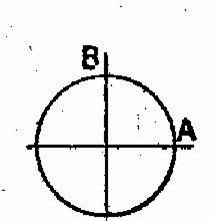
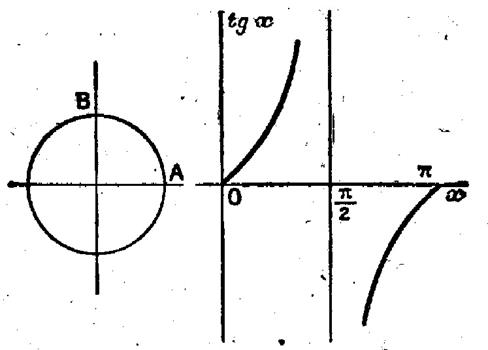
Le cercle trigonométrique
est un cercle orienté ayant pour rayon l’unité de longueur. (
R = 1 u) .
|
Sur un cercle trigonométrique , la mesure d’un arc , en radians, a pour valeur absolue la longueur de cet arc. Traçons ce cercle : Choisissons
une origine A pour les arcs et prenons : 1°) pour axe
X’X des abscisses la droite OA , orientée de O vers A 2°) pour axe
Y’Y des ordonnées l’axe déduit de X’X par une rotation de Ces axes
partagent le cercle en 4 quadrants, numérotés comme l’indique la figue
ci-contre. |
|
|
|
|
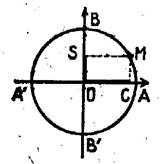
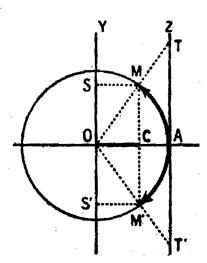
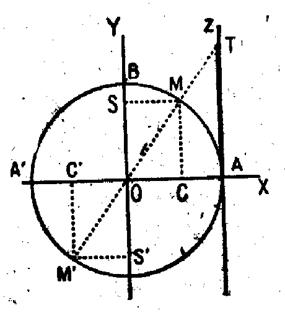
Soit M
l’extrémité de l’arc AM : noté
par la lettre « a » On
appelle : 1°) Cosinus de
l’arc a :
l’abscisse du point M ; cos a = 2°) Sinus de
l’arc a : l’ordonnée du point
M : sin a = Remarques : -
le cos a et le sin a sont
toujours compris entre -1 et +1. -
Le point C est la projection orthogonale de M sur l’axe X’X ; et le point S est la projection orthogonale
de M sur l’ax Y’Y. |
|
Périodicité :
Si
« a » augmente de ![]() , l’extrémité de revient au même point M ; le cosinus et
le sinus ne changent donc pas, on dit que cos a et sin a sont périodiques et de
période
, l’extrémité de revient au même point M ; le cosinus et
le sinus ne changent donc pas, on dit que cos a et sin a sont périodiques et de
période ![]()
Aussi :
|
|
Cos ( a + |
Et plus généralement |
Cos ( a + k. |
|
|
|
Sin (a + |
Et plus généralement |
Sin (a + k. |
|
|
|
|
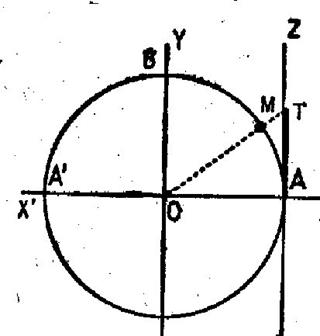
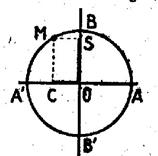
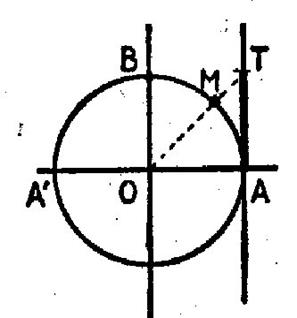
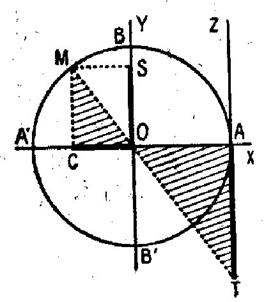
Menons par le
point A l’axe AZ parallèle à l’axe OY et de même sens ; Soit T le point où la droite OM (prolongée) , rencontre cet axe ( sur AZ) ; on appelle : 1°) Tangente
de l’arc a l’abscisse du point T sur l’axe
AZ ; 2°) Cotangent
de l’arc a l’inverse de sa tangente.
Ces deux
nombres algébriques peuvent prendre n’importe quelle valeur. |
|
Périodicité.
Si « a »
varie d’un multiple de π ( pi) , l’extrémité de
l’arc est en M ou au point diamétralement opposé, mais sa tangente et sa
cotangente ne change pas ; on dit que « tan a » et « cotan a » sont
périodiques et de période pi (π ) :
|
|
tan ( a + π ) = tan
a |
Et plus généralement |
tan ( a + k. π) = tan a |
|
|
|
co tan (a + π) = cotan a |
Et plus généralement |
cotan (a + k. π) = cotan a |
|
|
|
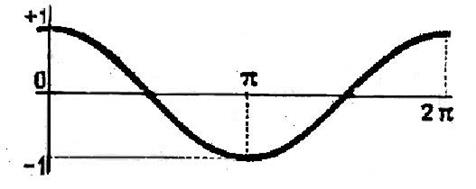
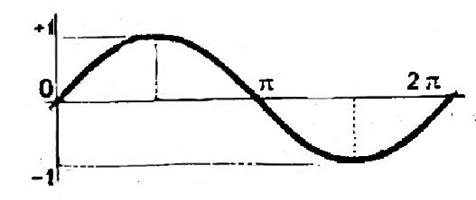
Chapitre 2 Fonction y = sin x
et y = cos x |
Info @ |
Ces fonctions sont
périodiques et de période ![]()
Nous allons
faire varier « x » la valeur de l’arc , dans
un intervalle d’amplitude ![]() , par exemple de 0 à
, par exemple de 0 à ![]()
Le
point M tourne dans le sens inverse d’une montre :
|
Premier
quart : Le sinus est
positif ; ( passe de la valeur : 0 à
+ 1 ) ; on dit que « le sinus croît » Le cosinus est
positif (passe de la valeur : +1
à + 0 )
; on dit que « le cosinus décroît » |
|
|
Deuxième quart : Le sinus est
positif (passe de la valeur : de +1 à O) ; on dit que « le sinus décroît » Le cosinus est
négatif (passe de la valeur : de 0 à -1 ) on dit que « le cosinus décroît » |
|
|
Troisième
quart : Le sinus est
négatif (passe de la valeur :de O à
-1) on dit que « le sinus décroît » Le cosinus est
négatif (passe de la valeur :de -1 à 0 ) on dit que « le cosinus croît » |
|
|
Quatrième quart : Le sinus est
négatif (passe de la valeur :de -1
à 0 ) on dit que « le sinus croît » Le cosinus est
positif (passe de la valeur : 0
à + 1 )
; on dit que « le cosinus croît » |
|
|
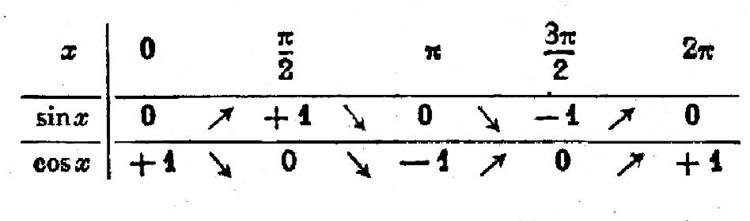
Ce qui est
résumé dans le tableau dit « de variation » ; ci contre : |
|
|
Courbe construite
, point par point , représentant la fonction cosinus x |
|
|
|
|
|
Info @ |
Courbe représentant la fonction
sinus x |
|
|
|
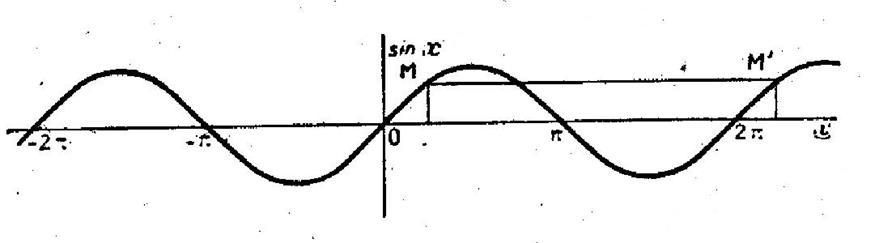
Si on fait
varier « x » de 2 π et 4 π , le sin x et
le cos x reprennent les mêmes valeurs.
Sur le graphique,
le point M’ d’ abscisse « x + 2 π » se
déduit du point M d’abscisse « x » par translation d’amplitude 2
π parallèle à « Ox ».
Les nouveaux
arcs de courbe se déduisent donc des précédentes par cette translation.,
|
Obtention de
la sinusoïde |
|
Il en est de
même si l’on fait varier « x » de 4 π à 6 π , de 6
π à 8 π ; de k (2 π) à (k+1 ) (2 π)
|
|
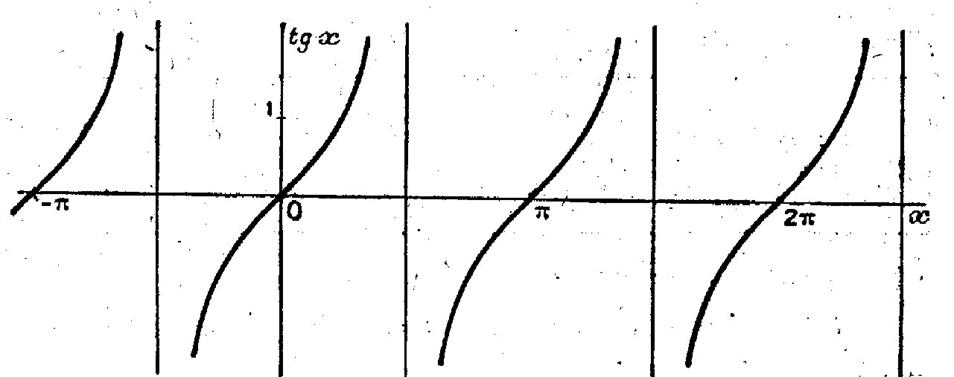
Fonctions y = tan x
et y = cotan
x |
|
En utilisant la même
méthode que ci-dessus : on déplace le point M sur le cercle…..
|
|
|
|
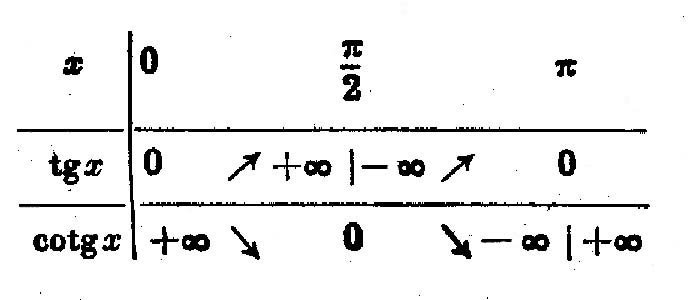
On fait varier
« x » entre 0 et π On obtient le
tableau de variation ci-dessous : |
|
|
|
|
On obtient la
représentation graphique de tan x : avec 0
≤
x ≤ π
|
|
|
Si on fait
varier « x » π en π , tan x ( et par conséquent cotan x )
reprennent les mêmes valeurs. , |
|
|
|
|
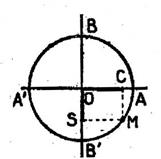
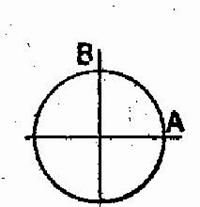
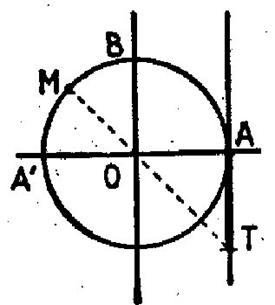
Fonctions circulaires d’un angle trigonométrique. |
|
|
Supposons cet
angle défini par sa mesure algébrique « a » ; ses fonctions
circulaires sont les mêmes que celles
de l’arc « a »,autrement dit , les mêmes
que celles de l’arc qu’il intercepte quand il est angle au centre. Voir
la figure ci contre. |
|
|
|
|
|
|
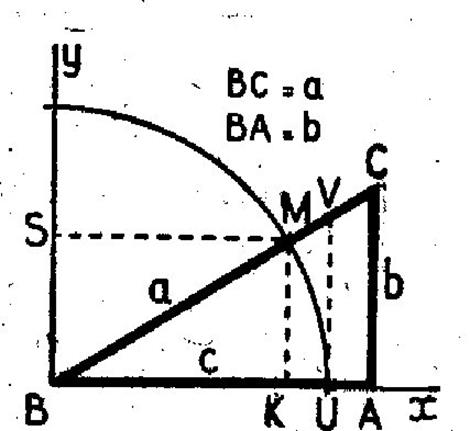
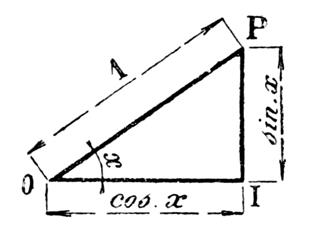
5-1 :
Application au triangle rectangle. Et le théorème : |
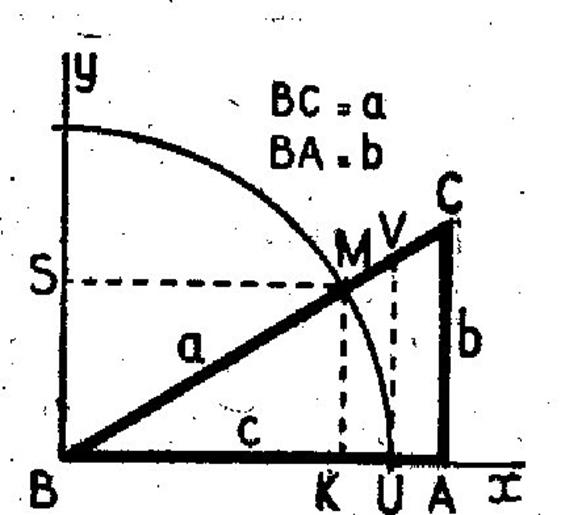
Reprenons la
figure ci-dessus.
|
Soit un
triangle ABC , rectangle en A . Mettons en
évidence sin B , cos B et tan B en traçant le cercle
trigonométrique de centre B ; on a , avec l’orientation voulue : Sin B = KM = BS Cos B = BK Tan B = UV Les triangles semblables donnent:
et
d’ où
ces égalités
peuvent s’écrire: b = a sin B ; c = a cos B
; b = c tan B ; c = b cotan B |
|
D’où
les formules :
Si
« x » est un angle aigu d’un
triangle rectangle :
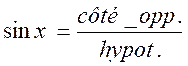 ;
; 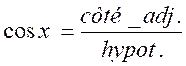 ;
;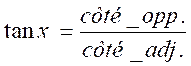 ;
;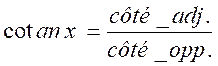
Théorème :
Dans
un triangle rectangle , un côté de l’angle droit est
égal :
1°)
A l’hypoténuse multiplié par le sinus de l’angle opposé ou par le cosinus de
l’angle adjacent ( au côté de l’angle que l’on
calcule) ;
2°)
A l’autre côté de l’angle droit multiplié par la tangente de l’angle opposé ou
par la co tangente de l’angle adjacent (au côté que
l’on calcule.),
|
|
5-2 : Application au triangle quelconque. |
Nous rappellerons les 3 formules
suivantes : (voir info + @)
1°) a² =
b² + c² - 2 bc cos A
2°) 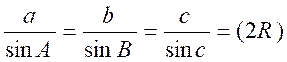
3°) 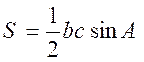
|
|
5-3 : «
Fonctions circulaires des arcs. : |
Info + @ |
|
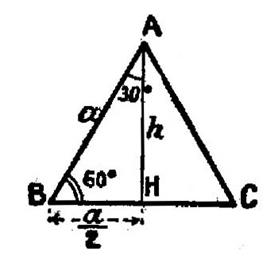
Les angles de
30° et de 60° s’obtiennent l’un de l’autre dans un demi triangle équilatéral. Rappelons la
formule importante : |
|
|
Les formules
ci- dessus donnent |
|
D’où ; après calculs |
||||||||
|
|
sin |
cos |
tan |
cotan |
|
|
sin |
cos |
tan |
cotan |
|
30° |
|
|
|
|
|
30° |
|
|
|
|
|
60° |
|
|
|
|
|
60° |
|
|
|
|
|
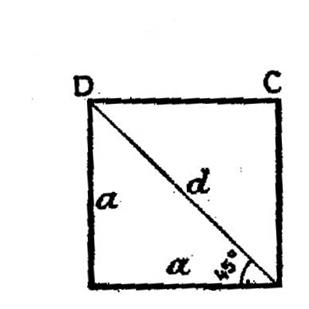
L’angle de 45°
s’obtient dans un triangle rectangle isocèle. Rappelle de la
formule importante Lcalcul de la diagonale) d = a la même
méthode donne :
|
|
|
|
5-4 Tableau récapitulatif. |
|
a |
0° |
30° |
45° |
60° |
90° |
|
|
Sin a |
0° |
|
|
|
1 |
Cos a |
|
Tan a |
0° |
|
1 |
|
|
Cotan a |
|
|
90° |
60° |
45° |
30° |
0° |
a |
Chapitre 6 : RELATIONS ENTRE LES
FONCTIONS CIRCULAIRES D’UN MEME ARC
Théorème : les
fonctions circulaires d’un même arc sont liées par les trois relations
suivantes :
|
|
angle x = a |
|
|
|
|
|
|
Relation 1 |
|
Relation 2 |
|
Relation 3 |
|
|
Cos² a + sin ² a = 1 |
|
|
|
|
|
Explications : |
|
|
Relation1 : Soit M
l’extrémité de l’arc .(figure ci
contre) Nous construisons ses fonctions circulaires. Dans le
triangle rectangle OCM : Or D’après
Pythagore : OC² + CM² = 1² ; 1²=
1 ; soit : OC² + CM² = 1 Donc :
Cos² a + sin ² a = 1 Relation
2 : Dans les
triangles homothétiques OCM et OAT,on
a
ou enfin (après transformation ) : Relation
3 : La troisième
relation résulte de la définition :
|
|
Activités :
Activité
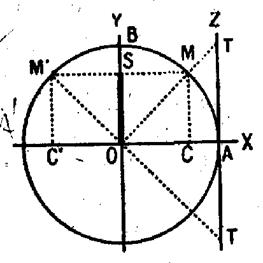
1 : Vérifier que les fonctions circulaires de 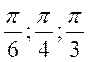 satisfont aux trois relations précédentes.
satisfont aux trois relations précédentes.
Activité 2 : Des rois relations précédentes ,
déduire les relations :
|
|
|
|
|
|
Activités
3 : Relations entre les fonctions circulaires d’un même arc.
Application :Un arc « x » compris entre 0 et ![]() est tel que tan x = 2
-
est tel que tan x = 2
- ![]() . Calculer le sin x et
le cosinus x.
. Calculer le sin x et
le cosinus x.
Réponse :
Les deux inconnues sin x et cos x sont données par les deux équations
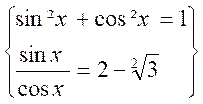
la deuxième relation se transforme
pour s’écrire : 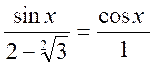
Nous élevons au carré
et nous opérons par combinaison proportionnelle :
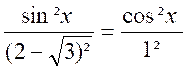 ;
; 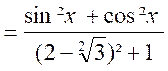
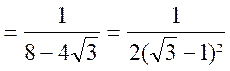
d’où puisque sin x et cos x sont
positifs :
|
|
|
|
|
|
|
|
(info @) Chapitre 7 :
ARC ASSOCIES ; LEURS
EXTREMITES ; LEURS FONCTIONS CIRCULAIRES.
A) Définition.
Pour abréger le
langage, nous appellerons « arcs associés » les arcs :
(arcs opposés)
: x et – x ; (arcs
supplémentaires) : x et (![]() - x) ; x et (
- x) ; x et (![]() + x) et les (arcs complémentaires) : x et (
+ x) et les (arcs complémentaires) : x et (![]() -x) ; x et (
-x) ; x et (![]() + x)
+ x)
B) Arcs
opposés : x et – x
On dit que deux
arcs sont opposés quand leurs mesures algébriques sont deux nombres
opposés : x et – x
Exemples :
|
|
+113° et – 113° |
+ 75 gr et – 75 gr |
|
Soit deux arcs
opposés d’origine A ; leurs extrémités sont évidemment sur une droite
parallèle à la droite contenant le diamètre OY. Donc : Nous citons le
théorème : Si deux
arcs sont opposés, ils ont le même cosinus , des
sinus opposés et des tangentes opposés. |
|
|
|
Cos (-x) = cos x |
|
Sin (-x) = - sin x |
|
|
|
|
|
Tan (-x) = - tan x |
|
Exemples :
|
|
|
|
C) Arcs supplémentaires : x et ![]() - x
- x
On
dit que : deux arcs sont supplémentaires quand la somme de leurs mesures
algébriques est ![]() (radians)
(radians)
Exemples :
|
|
42° et 138° |
- 103 gr et + 303 gr |
|
Soit deux arcs supplémentaires , x et On peut donc énoncer le théorème. Si deux arcs sont supplémentaires, ils ont même sinus, des cosinus
opposés et des tangentes opposées. |
|
|
Sin ( |
Cos ( |
Tan ( |
|
Exemple |
Exemple |
Exemple |
|
|
|
|
D) Arcs x et (![]() + x) :
+ x) :
Exemples :
|
|
123° et 323° |
335° et 535° |
|
Leurs extrémités
sont diamétralement opposés. donc : Tan ( Sin ( Cos ( |
|
E
) Arcs complémentaires : x et (![]() -x)
-x)
On dit que deux
arcs sont « complémentaires » quand leurs mesures algébriques ont
pour somme ![]() (radians)
(radians)
Exemples :
|
|
32° et 58° |
38 gr et 62 gr |
|
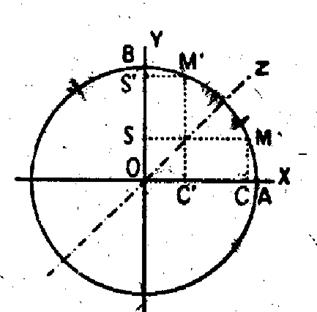
Soit deux arcs
complémentaires , x
et ( Comme OZ est
également axe de symétrie pour OX et OY, les vecteurs OC et OS’ , OC’ et le vecteur OS sont symétriques par rapport à
OZ, et ils ont deux à deux des mesures égales : |
|
|
|
C’est à dire |
Sin ( Cos ( |
|
On en déduit, par division membre à
membre: |
|
|
|
|
|
|
Tan (![]() -x) = co tan x et cotan
(
-x) = co tan x et cotan
(![]() -x) = tan x
-x) = tan x
Théorème :
Si deux arcs
sont complémentaires , le sinus de l’un est égal au
cosinus de l’autre ; la tangente de l’un est égale à la cotangente de
l’autre.
|
|
Sin ( |
Tan ( |
|
|
|
Cos ( |
cotan ( |
|
Activités :
vérifiez ce théorème pour les fonctions circulaires des arcs
complémentaires : 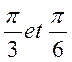 et
et 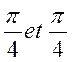
F) Arcs
complémentaires : x et (![]() + x)
+ x)
L’arc (![]() + x) a pour complément
(-x) ; donc
+ x) a pour complément
(-x) ; donc
|
Sin ( |
Cos ( |
Par division, on
obtient tan (![]() + x) et cotan (
+ x) et cotan (![]() + x)
+ x)
|
|
Sin ( |
Tan ( |
|
|
|
Cos ( |
cotan ( |
|
On aurait pu
remarquer aussi que (![]() + x) et (
+ x) et (![]() - x) sont
complémentaires.
- x) sont
complémentaires.
TRAVAUX AUTO _ FORMATIFS
CONTROLE:
A compléter…..
On dit que : deux arcs sont supplémentaires
quand la somme de leurs mesures algébriques est
![]() (radians)
(radians)