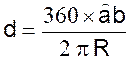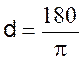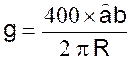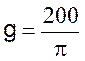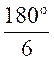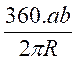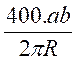Pré requis:
|
Angle au centre |
|
|
Unité d’angle (wrv) |
|
|
Cercle |
ENVIRONNEMENT du
dossier:
|
Objectif précédent : |
Objectif suivant |
||||
|
|
|||||
|
|
DOSSIER : Le RADIAN (symbole rd ) |
|
|||
|
|
1°) Définition. |
|
|||
|
|
2 °)
Conversion d’un radian en degré. |
|
|||
|
|
3°)
Conversion d’un radian en grades . |
|
|||
|
|
4°) Niveau IV : Il faut savoir ou savoir
retrouver ! ! ! |
|
|||
|
|
5°) Repérage des principaux nombres
« radians » dans le cercle : |
|
|||
|
|
|
|
|||
|
TEST |
COURS |
Interdisciplinarité 2°) le mouvement
circulaire uniforme. |
|
|
|
COURS
|
|
||||||||||||||||||||||||||||||||||||
|
|
Préambule : Le mot
« radian » a été imprimé pour la première fois en 1873.(les degrés avaient plus de deux mille ans d’ âge ) |
|
||||||||||||||||||||||||||||||||||||
|
|
1°)Définition. |
|
||||||||||||||||||||||||||||||||||||
|
|
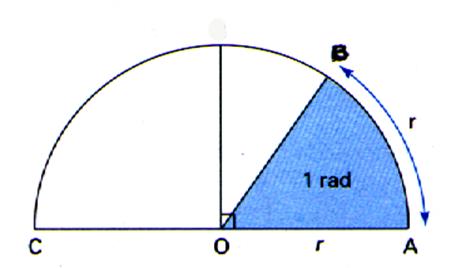
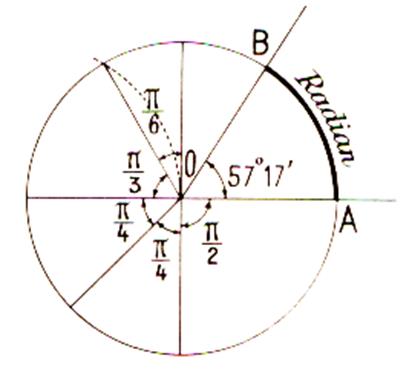
Par définition : le radian est l’angle au centre
qui intercepte sur la circonférence un arc égal au rayon. Arc AB
= rayon OA = 1 rayon = R
|
|
||||||||||||||||||||||||||||||||||||
|
|
Conséquences. On sait que : La circonférence à une
longueur de 2 ´p ´ R |
|
||||||||||||||||||||||||||||||||||||
|
|
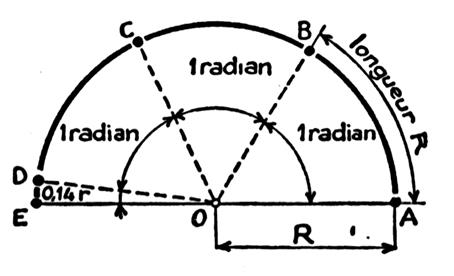
La demi - circonférence a une longueur de « p
R » ou « 3,14 R » L’angle plat AOE vaut donc : 3,14 R : R = 3,14 rd = p rd Donc un demi- cercle a pour mesure
p
radians. (ou 3,14 radians)
|
|
||||||||||||||||||||||||||||||||||||
|
|
On
retiendra : Un angle plat = 2 angles droits = 180 degrés = 200 grades = 3,14
radians Si l’angle plat vaut p
radians (angles ) ; l’angle droit le
cercle a pour mesure : 2 ´ p
radians (arcs) La lettre p (pi) que nous avons
souvent utilisée comme simple initiale pour désigner l’angle plat , pourra donc être considérée comme valant bien 3,
14159 … puisque l’angle plat p
vaut 3,14159…radians. l y a 2p radians (2 p rad ) dans
un cercle . |
|
||||||||||||||||||||||||||||||||||||
|
|
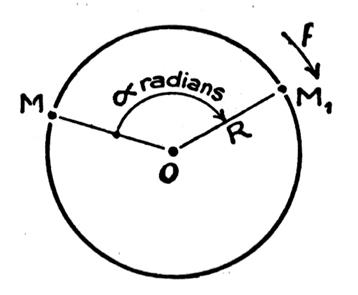
Dans un cercle de
rayon R , un angle au centre de 1 radian intercepte
un arc ab dont la longueur est ab = R ; Donc un angle au centre
de « α »
radians interceptera un arc dont la longueur est AB = Rα
|
|
||||||||||||||||||||||||||||||||||||
|
|
2 °)
Conversion d’un radian en degré :
|
|
||||||||||||||||||||||||||||||||||||
|
|
Calcul de l’angle , « en degré »
, au centre d’un arc «ab » dont
la longueur est égale au rayon : Formule : p #
57°18’ ;
ou 57° 17’45’’ |
|
||||||||||||||||||||||||||||||||||||
|
|
3°)
Conversion d’un radian en grades : |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
Calcul de l’angle , « en
grade » , au centre d’un arc ab dont la longueur est
égale au rayon : Formule : si l’on pose l’arc ab = R on obtient |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
On en déduit que : 180°
= p rad ; 90° = 60° = 45° = 30° = |
|
||||||||||||||||||||||||||||||||||||
|
|
4°) Niveau
IV : Il faut savoir ou savoir retrouver ! ! ! |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
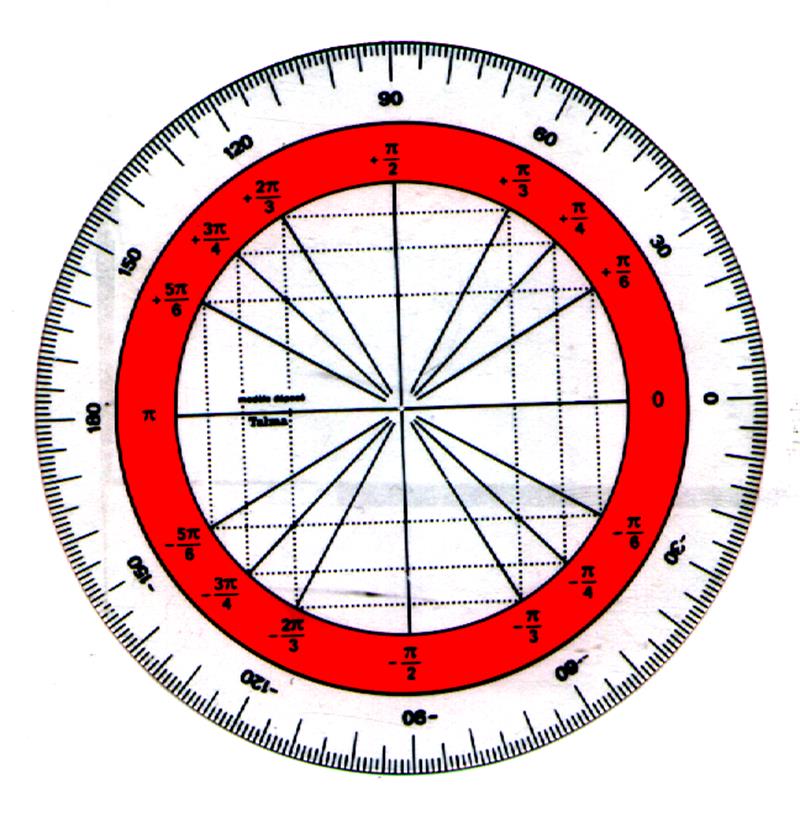
5°) Repérage des principaux nombres
« radians » dans le cercle : |
|
||||||||||||||||||||||||||||||||||||
|
|
Voir
leçon « le rapporteur » |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
Dans certaines questions , notamment en
trigonométrie , il est très commode de prendre pour unité d’arc AB dont la longueur est égale au rayon .(nous venons d’en calculer les mesures en degrés ou
en grades. En physique : (mouvement circulaire ) il est
commode d’utiliser comme unité d’angle, non pas le degré ou le grade , mais
le radian. la
longueur ( l )
parcourue par un point tournant autour d’un axe ( Rayon R) , l = R w ; w est
l’angle en radian ) |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
TRAVAUX AUTO
_FORMATIFS |
|
||||||||
|
|
|
|
||||||||
|
|
Donner la définition du radian : 1°) Calculez l’angle ,
« en degré » , au centre
d’un arc ab dont la longueur est égale au rayon : 2° )
Calculez l’angle , « en grade » , au
centre d’un arc ab dont la longueur est égale au rayon : 3°) tracer un demi cercle et reporter les
valeurs suivantes :
En artillerie , on prend pour unité d’angle
le millième , il s’agit du millième de radian. Pour un si petit angle , l’arc mesuré en
radians est égal à la tangente , qui vaut aussi 0,001 .Le milliradian
est donc l’angle sous lequel on voit
un segment vertical de |
|
|
|
CORRIGE
CONTROLE: Donner la définition du radian : L’ unité d’arc ab dont la longueur est égale au rayon s ‘
appelle « radian »
; on appellera aussi « radian » l’angle au centre AOB , que
l’on prendra en même temps pour unité d’angle. EVALUATION: 1°) Calculez l’angle ,
« en degré » , au centre
d’un arc ab dont la longueur est égale au rayon : Formule : d
= si l’on
pose l’arc ab = R on obtient
d = 2° ) Calculez l’angle , « en
grade » , au centre d’un arc ab dont la longueur est
égale au rayon : Formule : g
= si l’on
pose l’arc ab = R on obtient
g = 3°) tracer un demi cercle et
reporter les valeurs suivantes :
|
|
||||||||
|
|
|
|