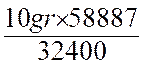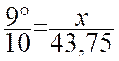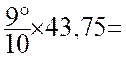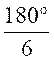|
Niveau V et IV |
Géométrie :
DOSSIER : Plan sous ensemble de plan
/ II / Objectif
cours 9 |
|||||||||||||
|
Pré requis: |
|
|||||||||||||
|
|
||||||||||||||
|
ENVIRONNEMENT
du dossier: |
||||||||||||||
|
Objectif
précédent : |
|
|||||||||||||
|
|
||||||||||||||
|
|
DOSSIER :LES UNITES d’ ANGLES |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
II ) les trois
unités de mesure d’un angle : |
|
||||||||||||
|
|
III ) CHANGEMENT
D’ UNITE « degré ;
grade » et
correspondances avec le
« radian »
|
|
||||||||||||
|
|
IV) Equivalence d’unité « degré ; grade » ; et correspondances
avec le « radian »
|
|
||||||||||||
|
|
Les trois unités usités sont
: |
|
||||||||||||
|
|
|
|||||||||||||
|
|
|
|||||||||||||
|
|
|
|||||||||||||
|
|
|
|
||||||||||||
|
TEST |
COURS |
|
||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
Un
angle est une grandeur :
(une grandeur : C’est un nombre associé à une unité) |
|
||||||||||||||||||||||||||||||||
|
|
I ) La loi du 14 janvier 1948 fixe pour unité légale de
mesure d’angle l’angle droit , ainsi défini : |
|
||||||||||||||||||||||||||||||||
|
|
« Angle
droit : est
un angle formé par deux droites se
coupant sous des angles adjacents égaux , il se représente sous le symbole « D » . » Il y a deux séries de sous multiples usuels légaux de l’angle
droit : 1°) le grade le grade ( gr), qui vaut 1/100 de D ; le décigrade (
dgr) , qui vaut 1/1 000 de D ;
le centigrade ( cgr) , qui vaut 1 / 10 000 de
D est désigné par « ‘ »
le milligrade ( mgr) , qui vaut 1/100 000 de D En outre , bien que ce ne soit pas légal , on
utilise pratiquement la seconde
centésimale qui vaut 1/ 1 000 000 de
D. est désigné par « ‘‘ » 2°) le degré le degré ( d
ou ° ) , qui vaut 1/90 de D la minute d’angle , ou « minute
sexagésimale » , qui vaut 1/60 D et désigné par « ’ » la seconde d’angle
, ou « seconde sexagésimale » , qui vaut 1/60 de minute est
désigné par « ’’ » |
|
||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||
|
|
Les
unités de mesure d’un angle
sont : |
|
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
Il y
a une « Relation » entre le cercle et la mesure d’un angle:
Remarque : Pour mesurer un angle on additionne des « arcs de
cercles » appelés « degré » ou « grade » ,mais on ne mesure pas des longueurs
de cercle. 1°)le degré (utilise comme système de numération , le
système sexagésimal) L’outil de mesure est un
rapporteur (cercle gradué
en degré ); le cercle est découpé en 360 parties
d'arcs égaux . L'angle droit mesure 90 degrés .
Cliquer ici : INFORMATION : table des
sinus ; cosinus ; …..
Pratiquement , le degré est employé pour toutes les mesures astronomiques , ainsi
que pour la navigation maritime et aérienne, parce que des rapports simples
existent entre les mesures de temps et les mesures en degrés ( 1 h correspond à 15°) |
|
||||||||||||||||||||||||||||||||
|
|
2°) le grade (utilise comme système de numération
, le système décimal) |
|
||||||||||||||||||||||||||||||||
|
|
L’outil de mesure est un rapporteur (cercle gradué en grades);le cercle est
découpé en 400 parties d'arcs égaux . L'angle droit
mesure 100 grades.
Cliquer ici : INFORMATION : table des
sinus ; cosinus ; ….. 3° le radian : (symbole rad ) Par définition : le radian ( symbole rad.)
est l’angle au centre qui intercepte sur une circonférence un arc égal au
rayon. AB = rayon OA = R
Cliquer ici : INFORMATION N°1
: table des sinus ; cosinus ; de degré et Radian…..
Cliquer ici : INFORMATION N°2 : table des
sinus ; cosinus ; de grade
et Radian….. L’outil
de mesure est un rapporteur (cercle
gradué en radian); le cercle est découpé en 2 p radian . L'angle
droit mesure le «2 p »
est obtenu en calculant la circonférence du cercle
de rayon valant « 1 » (calcul
de la circonférence du cercle = 2 p R ; si R vaut 1 ; nous obtenons 2 p Pratiquement le radian
est utilisé en sciences physiques,
notamment dans les études mettant en jeu les mouvements circulaires et
précisément dans les calculs qui font intervenir des vitesses angulaires.. Il est commode, en mécanique’ d’utiliser comme unité d’angle, non pas
le degré ou le grade, mais le radian. Ainsi : ►un
point lié tournant autour d’un point (centre) parcours une distance de 2 pi
radian ( on dit aussi que le point il a décrit un arc de 2 π .
radians ) ► et
on dit que la droite liant le centre à ce point à balayée un angle de 360° . (par exemple : voir les cadrans de radar des
aiguilleurs du ciel , qui guident les avions) . Si on considère que « pi = 3,14 » . ►
Donc on écrit que par équivalence que 2 π .
« radians » = 360° ► Si
2 π .
« radians » = 360° ;
alors π .radian =
180° ►
Pour « calculer la longueur »
ou « la distance parcourue »
par ce point , et à condition que l’on
connaisse la valeur du rayon du cercle (R ) , on remplacera « pi »
par « 3,14 » ce qui nous
donnera la formule (déjà connue) = 2 fois 3,14 fois R = 6,28
R |
|
||||||||||||||||||||||||||||||||
|
|
III ) CHANGEMENT D’ UNITE
« degré ; grade » et correspondances avec le
« radian »
|
|
||||||||||||||||||||||||||||||||
|
|
On passe d’un système à l’autre en tenant compte de
l’égalité fondamentale : 400 grades = 360 degrés. Il en résulte que 9 degrés (= 32
400’’) = 10 grades A) Première application :
transformer des degrés en grades
Exemple : transformer en grades 16° 21’ 27’’ Nous exprimons ( conversion)
en secondes la mesure de l’angle afin d’obtenir un nombre entier . Nous avons :
Nous savons que 9° = 32400’’ , ou à 10 gr. La réponse demandée est obtenue en faisant la règle de trois : |
|
||||||||||||||||||||||||||||||||
|
|
A) Première application : transformer des
grades en degrés .
|
|
||||||||||||||||||||||||||||||||
|
|
Exemple : Transformer
en degré , minutes et secondes 43,75 gr. La réponse est obtenue sous « forme décimale » en effectuant
la règle de trois A partir de D’ou x = Nous devons transformer en minutes et secondes la partie décimale de ce résultat : 0°,375 = 60’ 0,50 = 60’’ d’où le résultat suivant : 43,75 gr. =
39° 22’ 20’’ |
|
||||||||||||||||||||||||||||||||
|
|
IV) Equivalence
d’unité « degré ;
grade » et correspondances avec le « radian »
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||