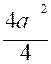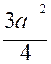|
Les droites
remarquables dans un triangle |
|
|
Angles |
ENVIRONNEMENT du
dossier:
|
NOTIONS dur les triangles vues
en primaire Autres cours à
consulter : |
NIVEAU V >> Programme 6 ème
|
||
|
|
|
|
|
|
Objectif
précédent : 1°) les triangles :
vu en primaire. 2°) Notions |
Objectif
suivant : 2° ) périmètre 3° ) Aire 4°) voir « le
sphéromètre » |
||
DOSSIER : LE TRIANGLE
EQUILATERAL
1.
Définition.
3.
Tracés
-
l’hexagone et triangle équilatéral
- calculs : hauteur et Triangle
équilatéral et rapports trigonométriques .
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
COURS
|
|
|
|
|
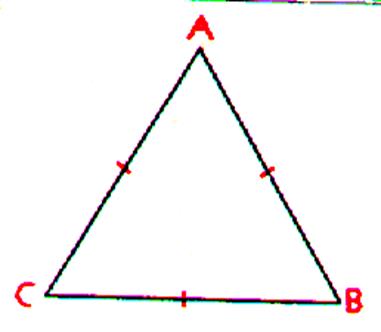
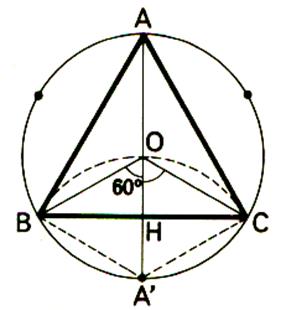
Un triangle équilatéral est un triangle qui a ses trois cotés égaux. AB = AC =BC |
|
|
|
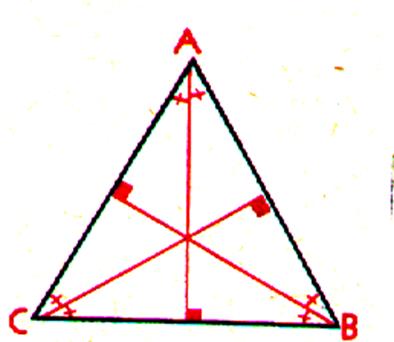
Remarque: Un triangle équilatéral est
"isocèle" de trois façons , donc : 1° les trois angles sont égaux: Chacun des angles vaut : 180° : 3 = 60° 3°) les trois médiatrices sont à la fois "hauteurs" , "bissectrices" et "médianes. Leur point d’intersection sont confondus . |
|
|
|
Voir +++++:les tracés
des droites caractéristiques
dans un triangle |
||
|
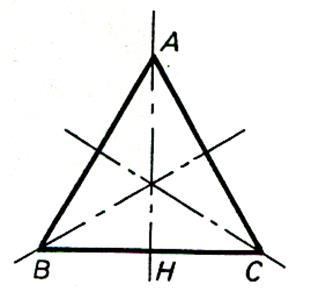
Les axes de symétries dans le triangle équilatéral |
|
|
Le triangle équilatéral possède 3 axes de symétrie. Ces axes sont les supports des trois médiatrices des côtés. |
|
|
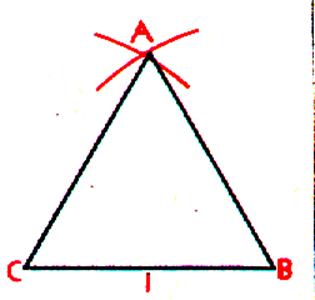
Construction
: On construit le coté BC qui a pour longueur la
longueur connue "1" , des points B et C comme centres avec un rayon égal à "1" on trace
deux arcs de cercles qui se coupent au point A , le triangle ABC est
équilatéral. |
|
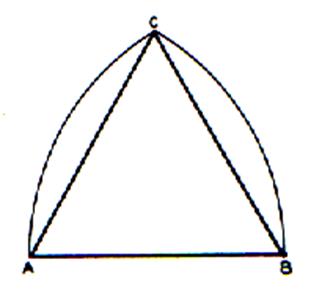
Connaissant la longueur du coté :
·
Tracer le segment AB . ·
Déterminer la position du point C avec un compas d’ouverture AB ;
placer la pointe du compas en B ; puis en A ; l’intersection des
arcs matérialise le point « C » |
|
|
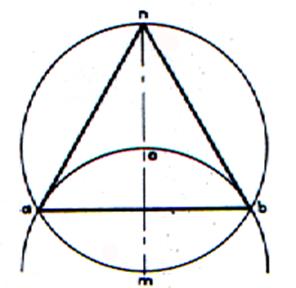
Connaissant le rayon du cercle
circonscrit . ·
Tracer le cercle et le diamètre « nOm » ; placer la pointe du compas en « m » ; en conservant le
rayon « on » ; ·
tracer « a » et « b » ·
Joindre « a »
à « b » ; « b » à « c » ; « a »
à « n » |
|
|
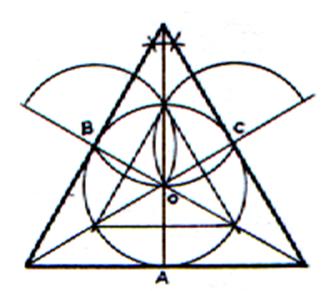
Connaissant le cercle inscrit . |
|
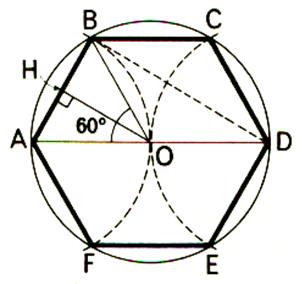
1°) Voir l’hexagone et triangle équilatéral
|
|
|
2°) Calculs
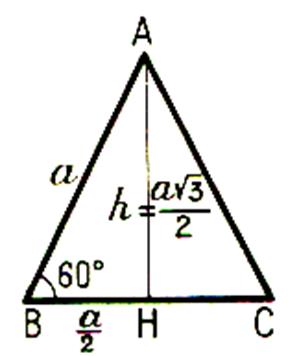
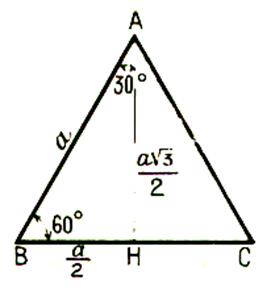
a) Hauteur d’un triangle équilatéral et Pythagore
|
a2 = ( a2 - ( a2 - h 2 = h 2 = h = |
|
b) Triangle équilatéral et rapports trigonométriques :
|
(
cos 30° = la
hauteur AH = |
|
CONTROLE :
1°) Quelles sont les caractéristiques du triangle équilatéral ?
2°) Quelle est la valeur des angles ?
3° ) Que peut-on dire sur les droites
caractéristiques (hauteurs ; médianes; médiatrices ; bissectrices )
4°) Que peut-on dire de la
position des points d’intersection de ces droites ?
EVALUATION
1 ) Tracer un triangle équilatéral
dont un coté mesure : 6 cm
2 ) Construisez sans rapporteur un
triangle équilatéral qui à pour hauteur 3 cm