Pré requis:
|
|
|||
|
|
|
||
|
|
|||
|
|
|||
ENVIRONNEMENT du
dossier:
|
Objectif précédent : |
Objectif suivant : Les
dérivées des fonctions circulaires |
Retour à la liste des objectifs de formation A
savoir : les abréviations : « tg »
et « tan » , abréviations :
lire « tangente » « cotg »
et « cotan » , abréviations :
lire « cotangente » |
DOSSIER : LES FONCTIONS CIRCULAIRES : ( résolutions de base)
Inégalités entre « sin x » ; « x » et « tan
x »
Résoudre :
-
les équations sin x = sin a. , et
application : Résoudre
l’équation sin ( 4x - ![]() ) = sin x ( en
radians)
) = sin x ( en
radians)
-
les équations cos x = cos a. et
application :
Résoudre l’équation cos ( 60 – 2x) = cos
( 4x +30) ( en degrés)
-
les équations tan x = tan a. et application : Résoudre l’équation : tan
( 7 x + 12 ) = tan ( 2 x + 62 ) (en grades)
|
TEST |
|
COURS
|
|
Inégalités entre « sin x » ; « x » et « tan
x » |
|
|
|
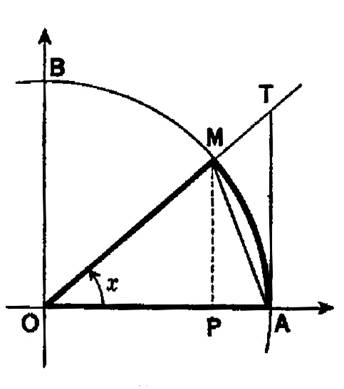
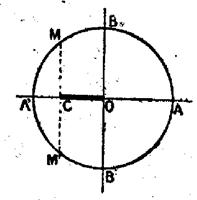
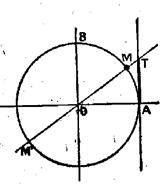
Sur le cercle trigonométrique , considérons l’arc Le point « M » se
projette en « P » sur l’axe « Ox » et la droite « OM »
coupe en « T » la tangente en « A » au cercle. On sait que : « cos x = 0P » ; « sin x = PM » ; « Tan x = AT » L’aire du secteur circulaire « OAM » est comprise entre celles
des triangles « OAM » et « OAT » . Donc : |
|
|
|
|
|
Problème 1
-
Résoudre l’équation sin x = sin a (en radians)
|
Soit M
l’extrémité de l’arc « a », Pour qu’un arc
ait Tous les arcs
terminés en M sont de la forme « a + k .2 L’équation sin
x = sin a admet donc deux familles de solutions : |
|
|
Sin x = sin a |
X= a + k .2 X = « k » est un entier
naturel |
On peut aussi
dire : pour que deux arcs aient le même sinus , il faut et il suffit
qu’ils soient égaux ou supplémentaires, à des cercles prés.
-
Application à un type d’équation.
Résoudre
l’équation sin ( 4x - ![]() ) = sin x ( en
radians)
) = sin x ( en
radians)
|
Pour que les arcs
( 4x - (1)
4x - (2)
ou 4x - 1°) l’équation
(1) donne : x = si
« k » varie d’un multiple de 3, « x » varie multiple de 2
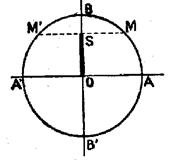
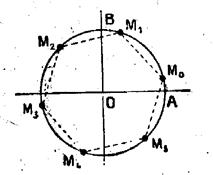
On aura donc
toutes les extrémités des arcs « x » en donnant à « k » trois
valeurs consécutives, par exemple 0 ;1 ;2 On a ainsi
trois extrémités d’arcs –solutions,aux sommets d’un triangle équilatéral.
(voir ci contre) |
|
|
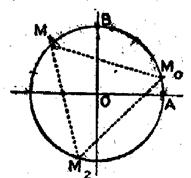
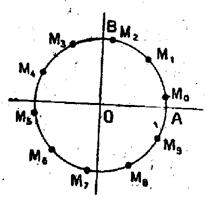
2°) L’équation
(2) donne x = d’où cinq extrémités
d’arcs- solutions,aux sommets d’un pentagone régulier. (ci contre) Ces cinq
nouveaux points sont différents des trois points trouvés précédemment, de
sorte que l’équation admet huit extrémités d’arcs – solutions. |
|
Problème
2 :
|
Résoudre l’équation
cos x = cos a ( en radians) . Soit M
l’extrémité de l’arc « a », Tous les arcs
terminés en M sont de la forme a + k .2 L’équation cos
x = cos a admet donc deux familles de solutions : |
|
|
cos x = cos
a |
X= a + k .2 X = « k » est un entier
naturel |
On peut dire
aussi :
Pour que deux
arcs aient le même cosinus,il faut et il suffit qu’ils soient égaux ou opposés,
à des cercles près.
Situation
exercice résolue :
Application à un
type d’équation. :
Résoudre l’équation cos ( 60 – 2x) = cos ( 4x +30) ( en degrés)
Cette équation
se dédouble en :
|
( 60 – 2x) = ( 4x +30) + k . 360 |
( 60 – 2x) = - ( 4x +30) + k . 360 |
|
60 – 30 – k .360= 4x +2x |
|
|
30 – 360 k = 6x |
|
|
x = 5 – k.60 |
x = - 45° + k . 180° |
|
|
|
|
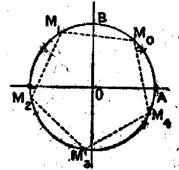
Les six extrémités d’arcs solutions , aux sommets
d’un hexagone régulier |
Deux extrémités
d’arcs solutions, sur la deuxième bissectrice. |
Soit en tout , huit extrémités d’arcs solutions.
Problème 3
Résoudre
l’équation : tan x = tan a (en radians)
|
Soit M
l’extrémité de l’arc « a » , Pour qu’un arc
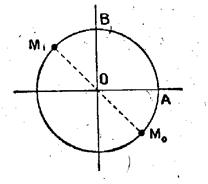
ait L’équation tan
x = tan a admet donc deux extrémités
d’arcs solutions : tan x = tan a ;
x = a + k On peut aussi
dire : Pour que
deux arcs aient la même tangente,il faut et il suffit qu’ils soient égaux,à
des demi-cercles près. |
|
Application à un
type d’équation :
|
tan ( 7 x + 12
) = tan ( 2 x + 62 ) (en grades) ( 7 x + 12
) = ( 2 x + 62 ) + k.200 x = 10 + k .40 soit : Dix extrémités d’arcs – solutions , aux sommets
d’un décagone régulier. |
|
Reste à refaire les
exercices proposés…….
TRAVAUX
AUTO _ FORMATIFS
CONTROLE:
A compléter…..
On dit que : deux arcs sont supplémentaires
quand la somme de leurs mesures algébriques est
![]() (radians)
(radians)
1°)
Résoudre l’équation sin ( 4x - ![]() ) = sin x ( en
radians)
) = sin x ( en
radians)
2°)
Résoudre l’équation
cos ( 60 – 2x) = cos ( 4x +30) ( en degrés)
3°) Résoudre l’équation : tan
( 7 x + 12 ) = tan ( 2 x + 62 ) (en grades)