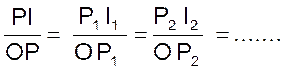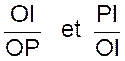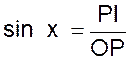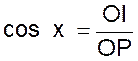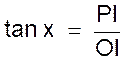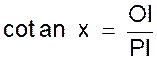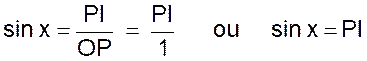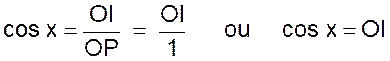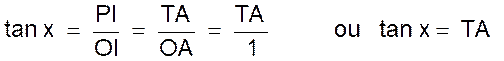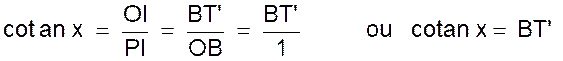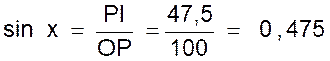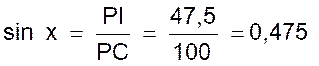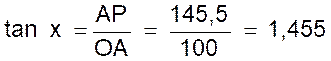Index warmaths

Liste des cours sur la trigonométrie.

TITRE : LES LIGNES TRIGONOMETRIQUES D’UN ANGLE AIGU et ses rapports trigonométriques.
		III ) INFORMATIONS «  formation leçon » :
Test	COURS		Travaux auto - formation.			Corrigé des travaux auto - formation.
			Contrôle	évaluation	INTERDISCIPLINARITE	Corrigé Contrôle		Corrigé évaluation
		Chapitres :					Info +++
		1°) Propriété fondamentale
		2°) Définitions des lignes trigonométriques
		3°) Remarque importante concernant une première approche sur le cercle trigonométrique)
		4°) Applications : construction d’angles connaissant le sinus et la tangente.					@ info +

Leçon	Titre L ES LIGNES TRIGONOMETRIQUES D’UN ANGLE AIGU.
N°3

	COURS
1°) Propriété fondamentale
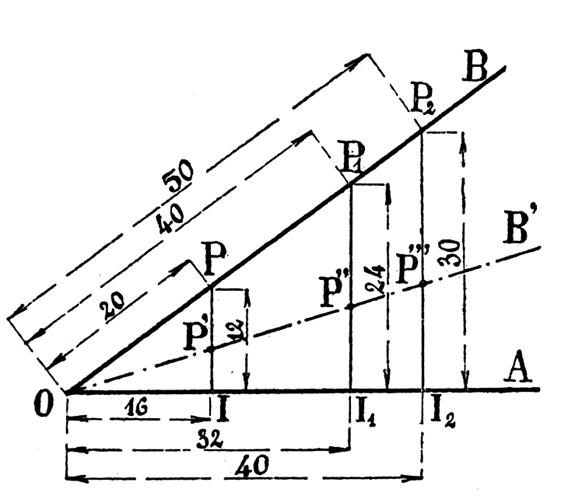
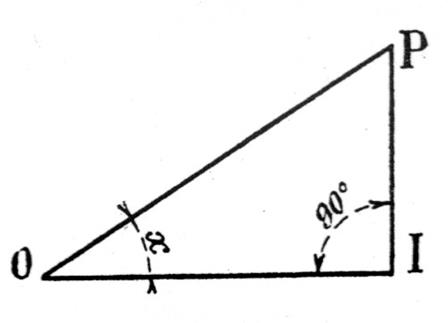
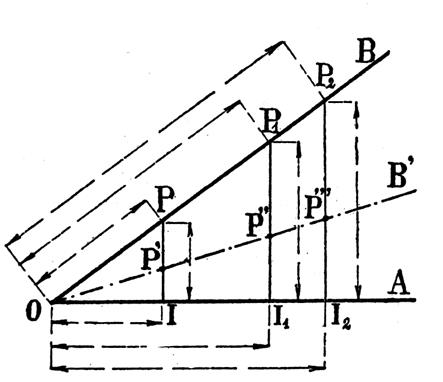
Voir la figure ci contre : Si l’on lace plusieurs points P ; P1, P2 ,….sur l’un des côtés d’un angle aigu et que l’on abaisse ( projette) de ces points des perpendiculaires PI ;, P1I1 , P2I2 sur l’autre côté OA , les triangles rectangles semblables obtenus ont leurs côtés correspondants ou homologues proportionnels et l’on peut écrire :
Le rapport a donc toujours la même valeur numérique quelque soit la position du point « P » sur « OB ». D’après les cotes de la figure ce rapport est ( à vous de recalculer)
Si l’on considère les autres rapports : , etc.…, obtenus avec d’autres segments de la figure on arrive à une conclusion identique :ces rapports sont constants par suite : Les rapports de deux des côtés de l’un des triangles ne dépendent nullement de la position du point « P », mais seulement de la grandeur de l’angle . Pour le 2^ème angle , par exemple , le rapport à une valeur différente de mais sa nouvelle valeur reste constante pour les diverses positions de P’ en P’’ , P’’’ , etc., sur OB’. Ces rapports sont donc caractéristiques de l’angle et vont nous permettre de définir ce que l’on entend par « lignes trigonométriques » » d’un angle .
2°) Définitions des lignes trigonométriques :
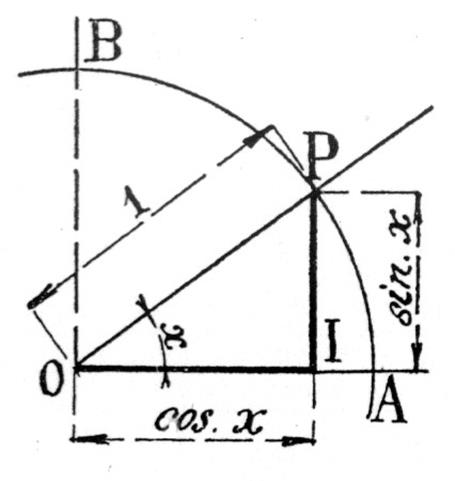
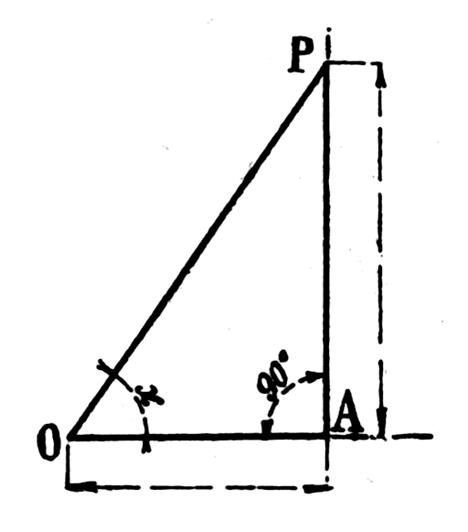
A ) Sinus d’un angle . « x » étant la valeur de l’angle exprimée par exemple en degrés , minutes et secondes ( on peut utiliser des valeurs d’angles exprimées en grades). , si l’un des triangles rectangles précédents POI est construit (ci contre),On appelle « sinus de l’angle « x » le rapport du côté « PI » de l’angle droit opposé à « x » , à l’hypoténuse « OP » et l’on écrit :
B ) Cosinus d’ un angle : le cosinus de l’angle x est le rapport du côté OI de l’angle droit adjacent à x , à l’hypoténuse OP et l’on écrit :
C) Tangente d’un angle : la tangente d’un angle x est le rapport du côté opposé à x à l’autre côté de l’angle droit et l’on écrit :
D) Cotangente d’un angle : la cotangente d’un angle x est le rapport inverse de celui mesurant la tangente du même angle et l’on écrit :
3°) Remarque importante : ( intro au cercle trigo)
Puisque les lignes trigonométriques définies par les rapports précédents ne dépendent pas de la longueur de OP, on peut prendre cette longueur égale à « l’unité » ( 1 cm , 1 dm , 1m °dans le but de simplifier les calculs et l’on écrit d’après la figure ci contre : 1°) 2°)
Le sinus et le cosinus d’un angle « x » ou de l’arc correspondant sont ainsi représentés par des segments rectilignes.
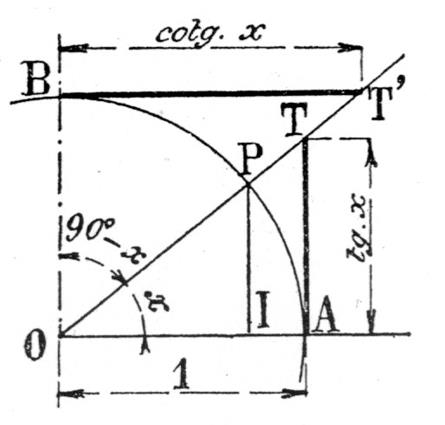
La même remarque et les propriétés des figures semblables permettent également de représenter la tangente et la cotangente d’un angle par des segments rectilignes. Si l’on décrit en effet un cercle de rayon « 1 » ( ce cercle est appelé « cercle trigonométrique ») du sommet « O » de l’angle comme centre (figure ci -contre) , la tangente et la cotangente sont respectivement représentées par les segments rectilignes AT et BT’ tangents au cercle aux extrémités « A » et « B » du quadrant
On a en effet en considérant les triangles rectangles semblables OPI et OTA : de même les triangles rectangles semblables OPI et OBT’ donne :
4°) APPLICATIONS : Constructions d’angles connaissant leurs lignes trigonométriques.
Les définitions des lignes trigonométriques d’un angle aigu permettent de construire un angle étant donné l’une de ses lignes trigonométriques. Dans ce qui suit , le problème est traité avec le sinus et la tangente
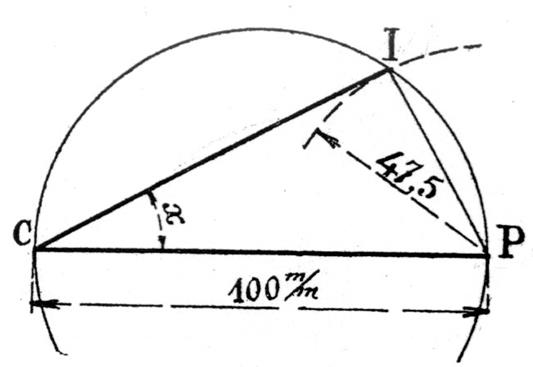
Premier exemple : (deux méthodes) Construire l’angle aigu « x » dont le sinus est égal à 0,475.
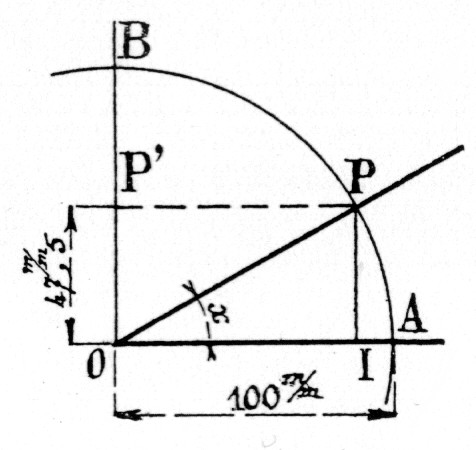
Première méthode : on décrit un cercle de centre o et de rayon unité. ( ci -contre) On prendra par exemple OA = 100 millimètres si l’exercice se fait sur feuille de dessin. Le quadrant OAB étant tracé , on porte sur OB un segment OP’ = 47,5 mm . La parallèle P’P à OA donne sur le cercle le point P que l’on joint au point O pour avoir l’angle « x » demandé car :
Nota : « 0,475 » : en utilisant des tables ou une calculatrice qui donnent les sinus des angles , on pourra trouver la valeur de cet angle et comparer cette valeur avec celle que donne la mesure au rapporteur de l’angle construit.
Deuxième méthode :
On décrit un cercle de diamètre CP = 100 millimètres (ci contre) et du point P comme centre avec une ouverture de compas égale à 47,5 mm , on décrit un arc de cercle coupant la circonférence O au point I ; l’angle cherché n’est autre que l’angle C formé par le diamètre CP et la corde CI car la figure ci contre donne encore , d’après la définition du sinus :
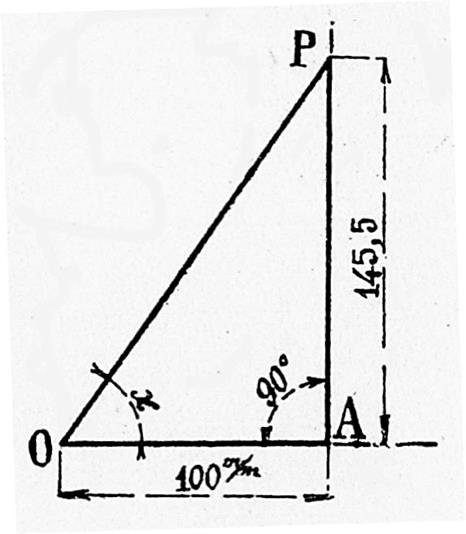
2^ème exemple : Construire l’angle x dont la tangente est égale à 1,455.
Sur une droite OX , on porte OA = 100 millimètres , par exemple. (figure ci contre) Au point A on élève la perpendiculaire et sur cette perpendiculaire on porte AP = 145,5 mm . En joignant P au point O on obtient l’angle cherché « x » car on a bien :
Cours suivant : les propriétés des lignes trigonométriques :

TRAVAUX AUTOFORMATIFS.
CONTROLE :
Citer les définitions des 4 lignes trigonométriques.
EVALUATION :
1°) Les tables et les calculatrices fournissant les valeurs des lignes trigonométriques donnent « 0 ,415 » pour valeur de sinus « 24° 30’ » . Comparer cette mesure avec celle que donnerait dans un cercle de rayon 100 millimètres , la longueur du sinus du même angle construit avec un rapporteur. ( niv V) 2°) Même exercice avec : tan 55° 30’ = 1,455 (niv VI) 3°) Même exercice avec : cos 37° 20’ = 0,795 (niv IV) 4°) Même exercice avec : cotan. 42° 40’ = 1,085 (Niv V) 5°) Construire l’angle aigu dont le sinus est 0,380. Mesurer l’angle au rapporteur et comparer le résultat avec le nombre de degrés fourni par les tables ou la calculatrice . ( 22°20’) 6°) Construire l’angle dont le cosinus = 0,824 7°) Construire l’angle dont la tangente = 1 , 220 8°) Construire l’angle dont la cotangente = 0,885
Niveau IV 9°) Le sinus d’un angle 4/5 = 0,800 . Calculer le cosinus et la tangente du même angle. 10°) Le cosinus d’un angle étant 0,550 , trouver ses autres lignes trigonométriques de l’angle. 11°) La tangente de l’angle = 1,6 , déterminer les autres lignes trigonométriques de l’angle. 12°) Le sinus d’un angle est les 3/4 de son cosinus . Trouver les lignes trigonométriques de cette angle et en donner la construction. 13°) On décrit entre les côtés d’un angle AOC un arc AC de 0,90 m de rayon et on trouve 0,60 m pour longueur de la perpendiculaire CP abaissée de C sur OA, quel est le sinus de l’angle ? Calculer ensuite le cosinus et la tangente du même angle. 14°) Montrer que quelque soit l’angle « a » ou a = sin (90° + a ) = cos a .
Travaux : valeurs à donner par le maître : et Calculer les rapports
OP
OP1
OP2
OI
OI1
OI2
PI
PI1
PI2
Calculer les rapports
OP	OP1	OP2	OI	OI1		OI2	PI	PI1	PI2
OP1
OP2
OI
OI1
OI2
PI
PI1
PI2
On, donne : PA = 0A = OP= Calculer : les lignes trigonométries :
Travaux : reprendre les exemples d’exercices traités dans le cours et les refaire !!!!!!
Leçon suivante : PROPRIETES DES LIGNES TRIGONOMETRIQUES .