Pré requis:
ENVIRONNEMENT du dossier:
|
|
|
|
Niveau 5 et 4 |
|
Objectif précédent : 1°) l’angle et sa mesure . |
|||
|
|
|
|
|
DOSSIER : ANGLES au centre et ANGLES INSCRITS
|
|
|
|
|
|
|
|
|
|
|
I )
DEFINITIONS : "Angle au
centre" et "angle inscrit" |
|
|||||
|
|
II
) POSITION
DES cotés par rapport a un cercle : (3cas) |
|
|||||
|
|
III) Valeur des angles . ( 3 cas) |
|
|||||
|
|
1er Cas : l’un des cotés
de l’angle inscrit passe par le centre
du cercle. |
|
|||||
|
|
2ème Cas : le centre du cercle est intérieur à
l’angle inscrit. |
|
|||||
|
|
3ème cas : le centre du cercle est à l’extérieur de
l’angle inscrit. |
|
|||||
|
|
|
|
|||||
|
|
IV) Deux angles inscrits qui interceptent les
deux arcs sous tendus par une même corde sont supplémentaires. |
|
|||||
|
|
Cas 1: L'angle |
|
|||||
|
|
Cas 2 : L'angle |
|
|||||
|
|
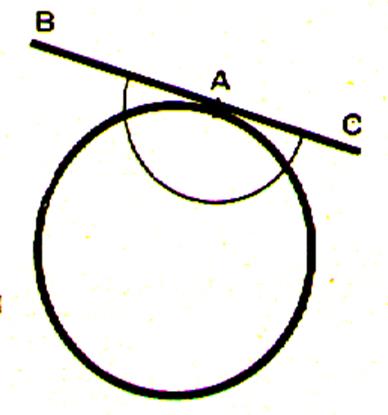
Cas particuliers : l’un des cotés de l’angle inscrit est tangent au cercle. |
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
COURS
|
A ) DEFINITIONS : "Angle au centre" et
"angle inscrit" |
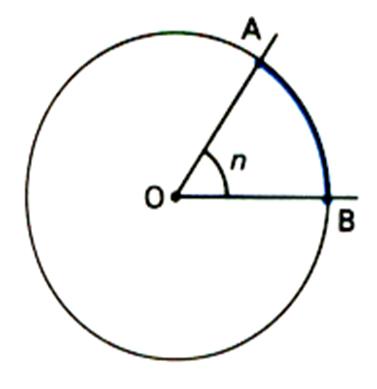
1°) ANGLE AU CENTRE :
Définition : Un angle au centre est un angle qui a son sommet au
centre d’un cercle .
|
La portion de cercle comprise entre les côtés d’un angle au centre est l’arc intercepté par cet angle . Exemple : l’angle au centre AOB ( |
|
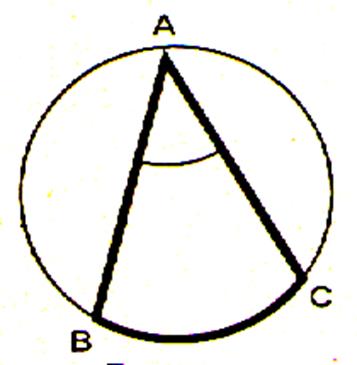
Définition: On appelle
"angle inscrit" à un disque, l'angle formé par deux cordes issues
d'un même point de la circonférence.
|
L'angle L'arc BC compris entre les côtés de l'angle inscrit est l'arc
"intercepté" par cet angle.( L'angle |
|
Autrement dit :
On
appelle « angle inscrit » dans un cercle un angle qui a son
sommet sur un cercle et dont les cotés sont sécants
ou tangents à ce cercle.
|
B ) POSITION DES COTES : (3cas) |
|
|
a)
Les deux
cotés passant par B et C sont sécants
au cercle: |
|
|
L’angle inscrit |
|
|
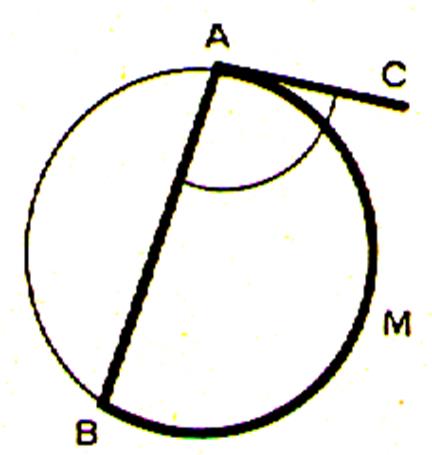
b)
Un coté sécant,
l’autre tangent : |
|
|
L’angle inscrit BAC intercepte l’arc BMA |
|
|
c)
Les cotés sont
tangents : |
|
|
L’angle inscrit BAC intercepte le cercle. |
|
|
II) Valeur des
angles : |
Théorème : la mesure d'un angle inscrit est égal à la moitié
de la mesure l’angle au centre correspondant
(qui intercepte le même arc) .
|
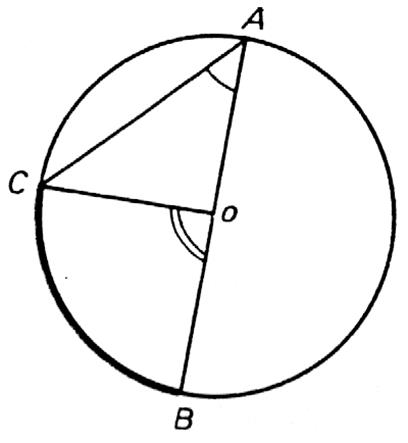
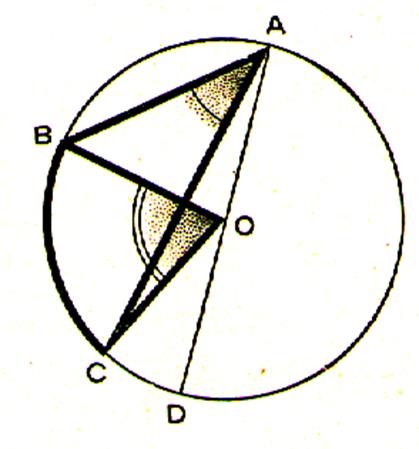
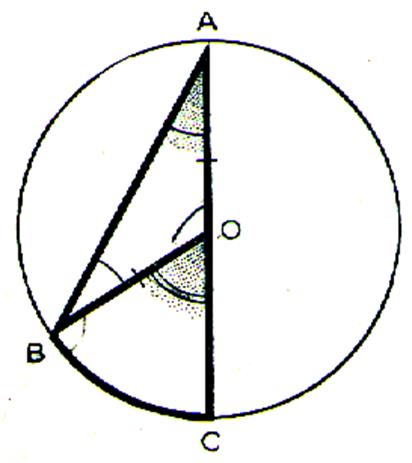
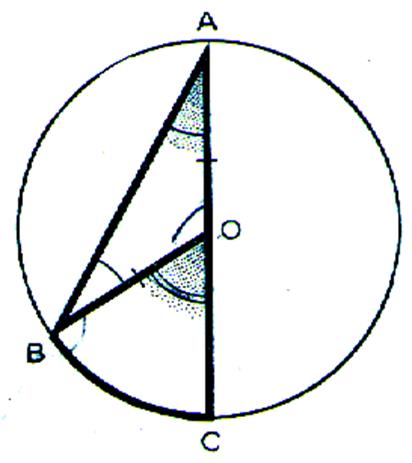
1er Cas : l’un des cotés
de l’angle inscrit passe par le centre
du cercle. |
|
|
L'un des côtés est un diamètre. Le triangle AOC est isocèle donc : L'angle Mes. mes. |
|
|
Activité : Quel est le cas étudié? |
|
|
Compléter la phrase. l’angle |
|
|
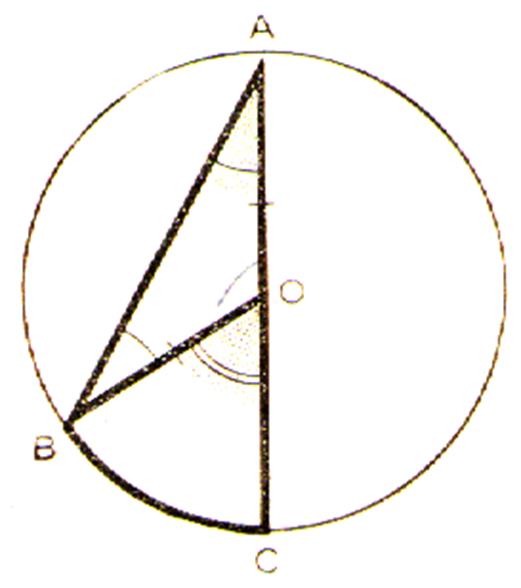
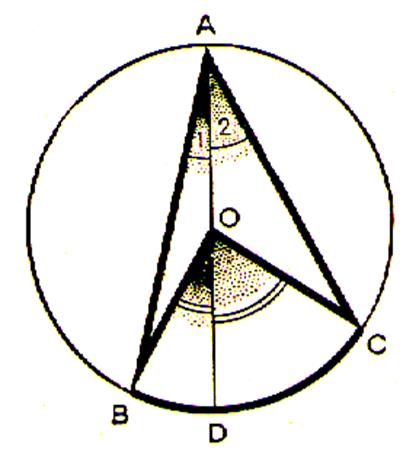
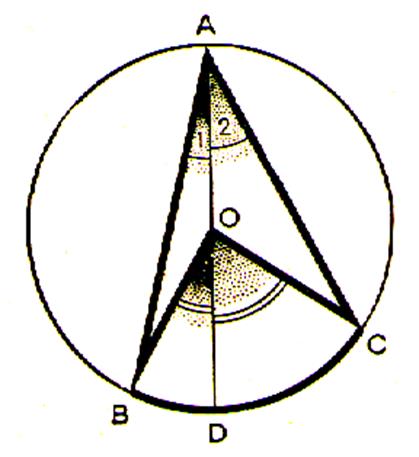
2ème Cas : le centre du cercle est intérieur à
l’angle inscrit. |
|
|
Soit AD le diamètre passant par A, d'après ce qui précède : mes. mes. en additionnant membre à membre il vient : mes. |
|
|
Activité : Quel est le cas étudié ? …………………….. |
|
|
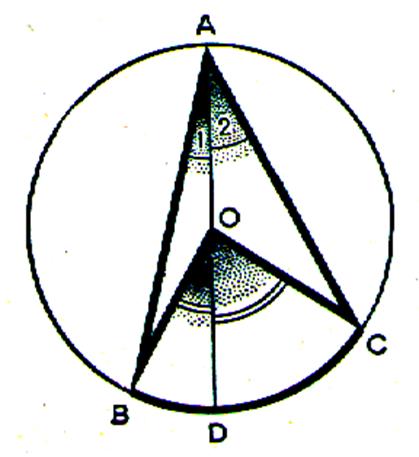
compléter les phrases.: L’angle A1 est égal
à l’angle ……. L’angle A2 est égal
à l’angle ……. L’angle BAC est à la somme des angles ……………. qui est égal à l’angle BOD divisé par deux
plus l’angle DOC divisé par deux . Ainsi l’angle BAC est égal à l’angle …………
divisé par deux . |
|
|
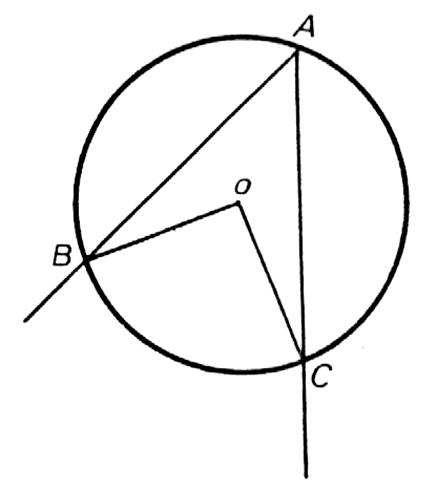
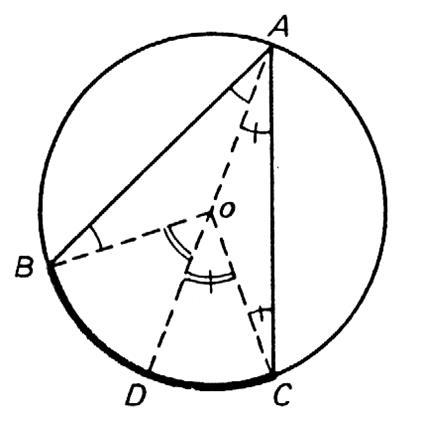
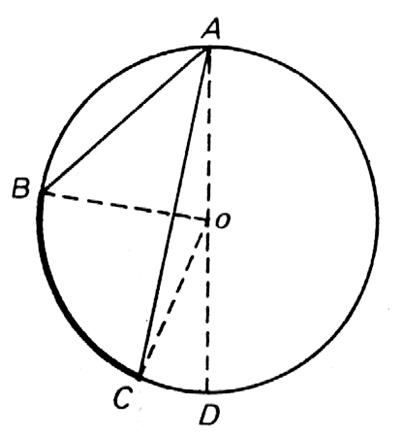
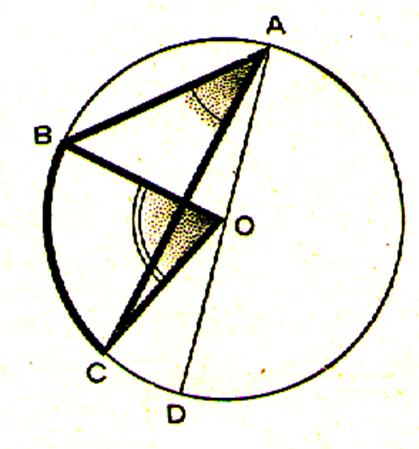
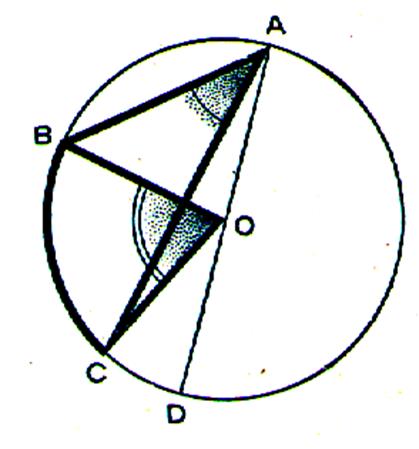
3ème cas : le centre du cercle est à l’extérieur de
l’angle inscrit. |
|
|
Soit AD le diamètre passant par A. mes. mes. en retranchant membre à membre il vient : mes. mes. |
|
|
Activité
: Dans quel cas sommes nous ? |
|
|
On donne le diamètre AOD. Compléter les phrases suivantes: L’angle BAD = l’angle ….. L’angle CAD = l’angle ……… L’angle BAC = l’angle BAD – l’angle CAD = ( l’angle BOD – l’angle COD) divisé par 2 . L’angle BAC = l’angle ………… |
|
|
Conséquences : |
1. Deux angles inscrits qui interceptent le même arc ou des arcs
isométriques sont isométriques.
2. Deux angles isométriques inscrits dans un même disque ( ou dans deux disques isométriques) interceptent des arcs
isométriques.
Ces arcs en effet sont interceptés par des angles au centre isométriques.
|
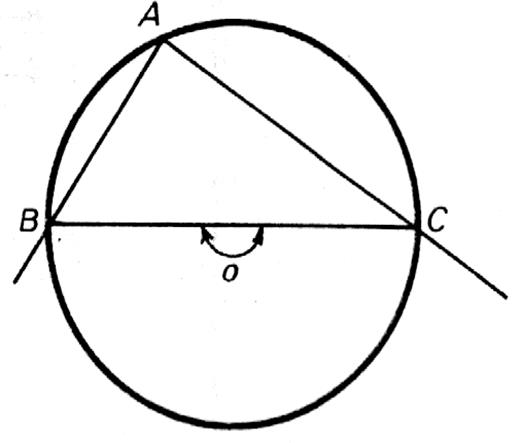
3. Tout angle inscrit dans un demi disque est un angle droit. On a toujours: mes. comme ici : mes. Il vient mes. |
|
|
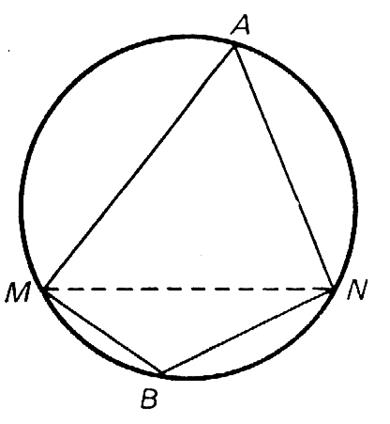
IV) Deux angles inscrits qui interceptent les
deux arcs sous tendus par une même corde sont supplémentaires. |
|
|
Soient les deux angles inscrits La somme des deux angles inscrits est donc égale à 180°. |
|
5.L'angle formé par une tangente et une corde ,
issue d'un même point, est isométrique
de la moitié de l'angle au centre correspondant. ( 2 cas)
|
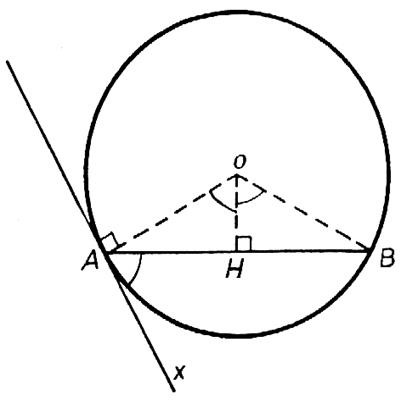
Cas 1: L'angle |
|
|
Mes. Le triangle BOA est isocèle, donc, mes. mais mes. donc: mes. |
|
|
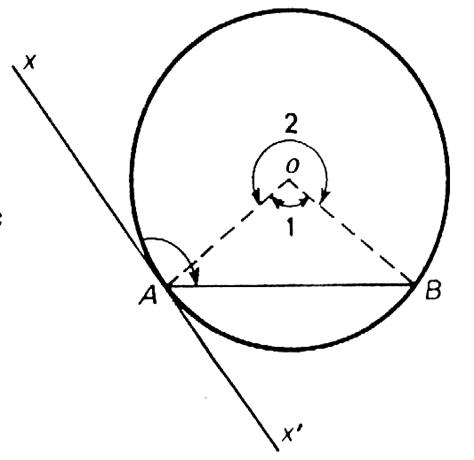
Cas 2 : L'angle |
|
|
mes. On vient de voir que : Mes. Or , On en déduit que mes. |
|
|
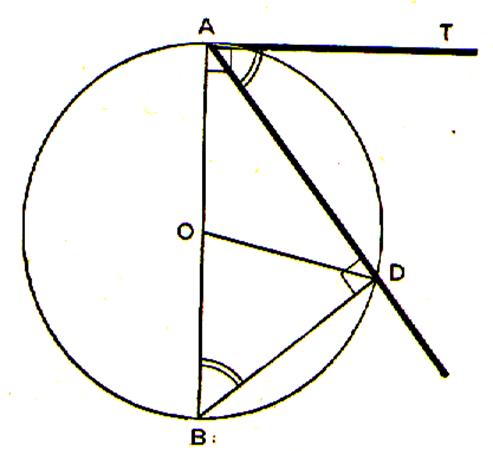
Cas particulier : l’un des cotés de l’angle inscrit est tangent au cercle. |
|
|
Soit l’angle TAD que nous supposerons aigu (le centre du cercle est à
l’extérieur de l’angle). Traçons le diamètre AOB. Les angles TAD et ABD sont égaux car, tous
deux aigus, ils ont leurs cotés respectivement
perpendiculaires. D’où l’angle TAD = à l’angle ABD = l’angle AOD divisé par 2. |
|
CORRIGE DES ACTIVITES:
|
Activité 3: Dans quel cas sommes nous ? le centre du cercle
est à l’extérieur de l’angle inscrit. |
|
|
On donne le diamètre AOD. Compléter les phrases suivantes: L’angle BAD = l’angle BOD divisé par 2. L’angle CAD = l’angle COD divisé par 2 . L’angle BAC = l’angle BAD – l’angle CAD = ( l’angle BOD – l’angle COD) divisé par 2 . L’angle BAC = l’angle BOC divisé par 2. |
|
|
Activité 2: compléter les phrases. Quel est le cas étudié ? le centre du cercle est à l’intérieur de l’angle inscrit. |
|
|
L’angle A1 est égal
à l’angle BOD divisé par deux . L’angle A2 est égal
à l’angle DOC divisé par deux . L’angle BAC est à la somme des angles A1
+ A2 qui est égal à
l’angle BOD divisé par deux plus l’angle DOC divisé par deux
. Ainsi l’angle BAC est égal à l’angle BOC
divisé par deux . |
|
|
Activité 1: Quel est le cas étudié? l’un des cotés de l’angle inscrit
passe par le centre du cercle |
|
|
A quel angle est égal l'angle BAC ? l’angle BAC est égal à l’angle BOC divisé par deux. |
|
Travaux auto formatifs.
CONTROLE:
1° )
Qu’appelle t – on « angle au
centre » ?
2° )
Qu’appelle t – on « angle
inscrit » ?
3° )
Compléter les phrases suivantes :
un angle inscrit dans un demi
cercle est …………
Deux angles inscrits dans
un même cercle et interceptant le même arc sont ……….
SERIE 1:
|
Activité 1: Dans quel cas sommes
nous ? |
|
|
On donne le diamètre AOD. Compléter les phrases suivantes: L’angle BAD = l’angle …………. L’angle CAD = l’angle …………… L’angle BAC = l’angle BAD – l’angle
CAD = (
l’angle BOD – l’angle COD) divisé par 2 . L’angle BAC = l’angle …………….. |
|
|
Activité 2 : compléter les phrases. Quel est le cas
étudié ? |
|
|
L’angle A1 est égal à l’angle ………………………………… L’angle A2 est égal à l’angle ……………………………………. L’angle BAC est à la somme des angles ……………….. qui
est égal à l’angle BOD divisé par deux plus l’angle DOC divisé par deux . Ainsi l’angle BAC est égal à l’angle …………….. divisé par deux . |
|
|
Activité 3 : Quel est le cas étudié? |
|
|
A quel angle est égal l'angle BAC ? l’angle BAC est égal à l’angle ………………………. |
|
2°) Un angle au centre a pour mesure 108° ; quelle est la mesure
d'un angle inscrit qui intercepte le
même arc?
3°) Un arc AB vaut 1/10 de la
circonférence, les tangentes au disque
en A et B se coupent en C .
a)quelle est la mesure de l'angle au
centre correspondant?
b)Calculer la valeur des angles du triangle ABC .