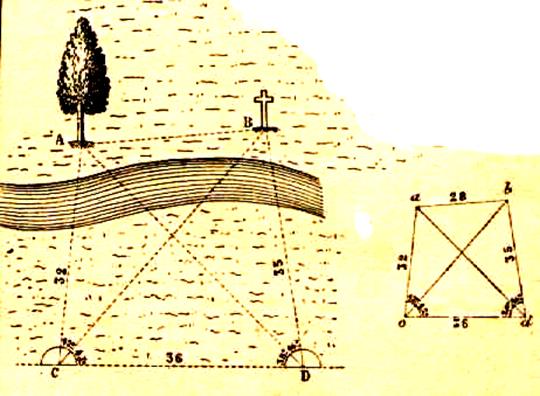
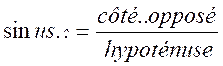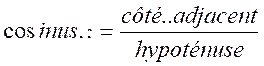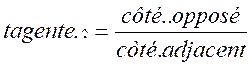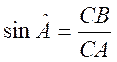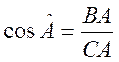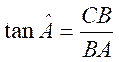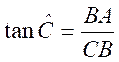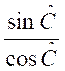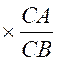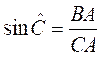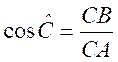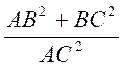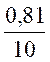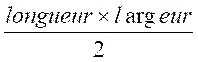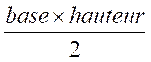|
Pré requis: |
Revu le 12 /sept.11 |
|||||||||||
|
Le triangle rectangle |
||||||||||||
|
Système métrique |
||||||||||||
|
ENVIRONNEMENT du dossier: |
||||||||||||
|
Objectif précédent 1°) Voir
formulaire 2°) les relations trigonométriques dans un triangle
rectangle. |
Objectif suivant |
tableau |
||||||||||
|
|
|
|
|
|||||||||
|
DOSSIER :
niveau V (BEP) RELATIONS
METRIQUES du TRIANGLE RECTANGLE -
Propriétés de
Pythagore. -
Les relations
trigonométriques dans le triangle rectangle. |
||||||||||||
|
TEST |
COURS |
Devoir Contrôle |
Interdisciplinarité |
|
Corrigé Contrôle |
Corrigé
évaluation |
||||||
|
|
||||||||||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
COURS
|
||||||||||||
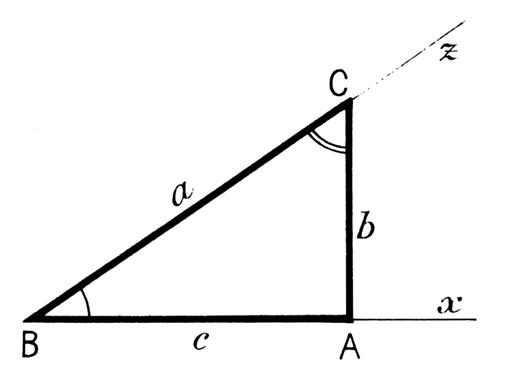
I ) propriétés
de Pythagore
|
||||||||||||
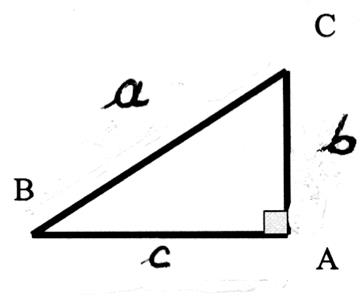
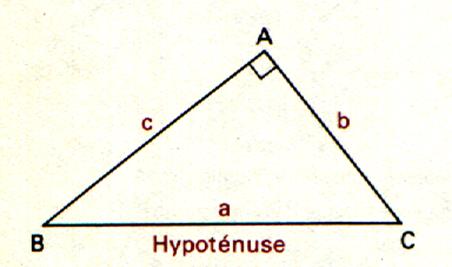
Théorème : Dans un triangle rectangle : le
« carré » de la longueur de l’hypoténuse (c’est à dire : la
longueur de l’hypoténuse multipliée par la longueur de l’hypoténuse) est égal
à la somme des « carrés » des longueurs des cotés (du triangle) formant l’angle
droit.
b ) si l’on nomme les cotés par des lettres. :
|
alors on peut écrire : (BC ) ² = (BA)² +
( AC ) ² si BC = a ;
BA = b ; AC = c ou a2
= b2 +c2 |
|
|
a ) si l’on nomme les sommets du triangle , par une lettre : (
A ; C et B angle droit )
AC désigne
la longueur de l’hypoténuse. AB désigne
la longueur d’un coté
formant l’angle droit BC désigne
la longueur d’un coté
formant l’angle droit |
|
On peut écrire , d’après « Pythagore » :
AC fois AC =
AB fois AB + BC fois BC
soit : AC2 = AB 2 + BC 2
2 ) Propriété réciproque :
Soit un triangle ABC : si AC2 = AB 2 + BC 2 alors
ABC est un triangle rectangle en B.
Exemple 1 : soit un triangle dont on
relève les mesures : 50 ; 30 ; 20
Vérifier , en calculant
si 502 = ? = 30 2 + 20 2 ? alors , d’après la réciproque de Pythagore , on ne peut pas affirmer que le triangle
est « rectangle ».
Exemple 2 : soit un triangle dont on relève les
mesures : 50 ; 40 ; 30
si 502 = 40 2 + 30 2 alors , d’après la
réciproque de Pythagore , affirmer que
le triangle est « rectangle ».
II ) RELATIONS TRIGONOMETRIQUES :
|
1°) Mesure des
angles : |
Pré requis |
Les Unités d’angles : elles sont référencées par le système International
Le radian ( rad) est
l’unité légale du système international utilisé pour l’étude des mouvement
circulaire .
Le degré ( ° ) est l’unité
la plus souvent utilisée en géométrie .
Le grade (gr ) est l’unité
utilisée dans certains métiers.
Conversions :
Si « x » désigne la mesure d’un angle en degrés , « y » sa mesure en radian et « z » sa mesure en
grades , alors on peut établir les relations de proportionnalité suivantes :
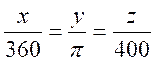
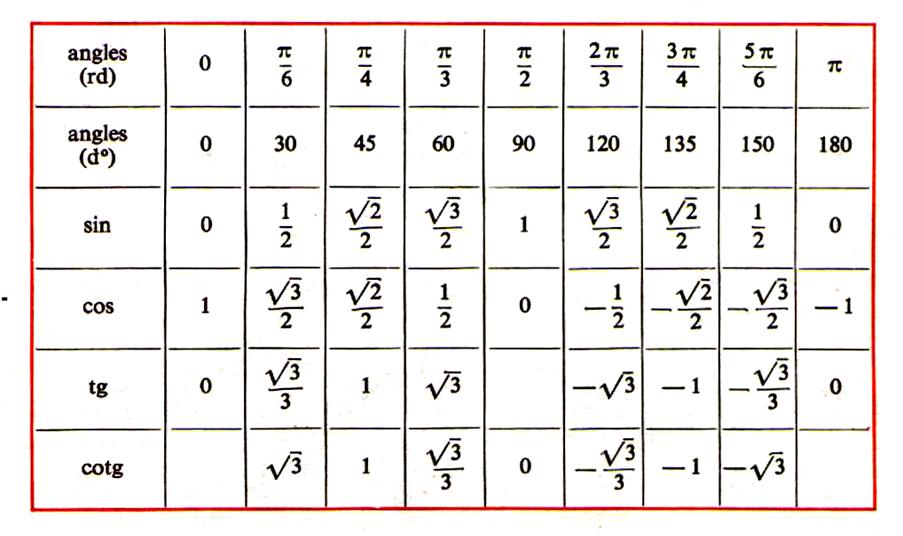
Angles remarquables :
|
( ° ) |
0 |
30 |
45 |
60 |
90 |
|
( rad ) |
0 |
|
|
|
|
|
2°) Rapports trigonométriques |
|||
|
Les rapports trigonométriques ont pour but
d’établir des relations entre les côtés
et les angles d’un triangle rectangle . C’est après avoir choisi l’angle aigu que l’on
détermine le côté opposé et le côté adjacent . |
|||
|
|
|
|
|
|
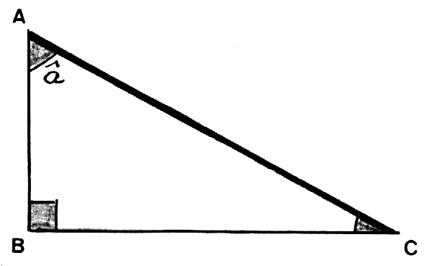
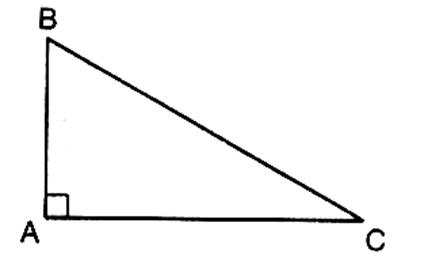
Ainsi dans le triangle rectangle en B , par rapport à l’angle |
|||
|
CB est le côté opposé à l’angle A
et BA le côté adjacent à l’angle A . Les rapports trigonométriques permettent d’établir les relations :
|
|
|
Voir exercices |
|
||||
|
remarque :on
obtiendrait des relations similaires avec l’angle « C ». ainsi : |
|||||
|
|
|
|
|||
|
III )PROPRIETES : |
|||||
|
1° ) Les angles complémentaires |
Pré requis : |
||||
|
Pour un même triangle nous avons obtenu les
égalités suivantes :
on remarque que : de même que On sait que
Conclusion : le sinus et le cosinus de
deux angles complémentaires sont égaux |
|||||
|
2° )
relation entre tangente , sinus et cosinus : |
Pré requis : |
||||
|
La tangente d’un
angle est égale au rapport du sinus sur le cosinus de l’angle considéré. Explications :
on veut montrer que |
|||||
|
|
|||||
|
Nous avions trouvé
précédemment que : On pose :
calculs ( SOS rappels) :
ainsi :
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
3° ) relation entre sinus et cosinus : |
Pré requis : |
||||
A C B
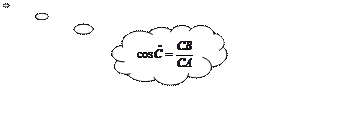
D’après « Pythagore » : AC 
= AB+ BC
On
sait que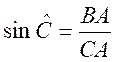 
; 
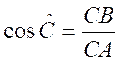
on peut
écrire : 1 = (
) + (
)
|
Transformations : ( |
L’égalité : () + ()=
(
) + (
)
Devient l’égalité () + ()=
+ 
|
( |
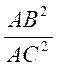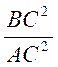
Or d’après
« Pythagore » : AC = AB+ BC
- On remplace dans l’égalité précédente AB+ BCpar
: AC
- Nous obtenons une nouvelle égalité : () + ()=
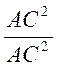
puisque 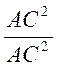= 1 , on peut écrire que :
() + ()= 1
CONCLUSION :la somme des carrés
du sinus et du cosinus d’un angle est
égal à 1
|
Pour en savoir plus : |
IV ) Valeurs trigonométriques des angles
remarquables . (info
@ +)
Entre 0° et 90° (le quart de cercle)
|
|
0° |
30° |
45° |
60° |
90° |
|
sin a |
0 |
|
|
|
1 |
|
cosa |
1 |
|
|
|
0 |
|
0 |
|
1 |
|
|
·
faire
le calcul (SOS rappel) :
= 
·
Entre 0° et 180°
|
En plus ++++ graduation
d’un cercle. |
|
Entre 0° et 180° :(le
demi cercle) |
|
|
Entre
0° et 360° ……
|
En plus
++++ graduation d’un cercle. |
V )
Construction et mesure d’un angle :
|
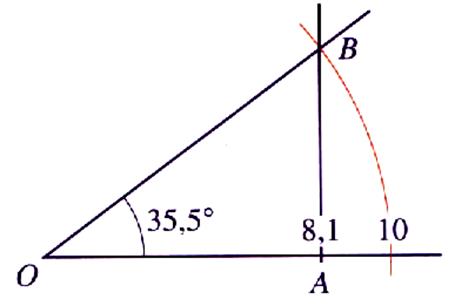
On recherche le cosinus de 35,5° : » 0,81 soit = procédure de tracé : -tracer un arc de rayon 10 cm ; -
sur [ 0x) placer le point « A » tel que OA = 8,1 cm -
tracer une
perpendiculaire à [ 0x) passant par « A »
et coupant l’arc de cercle en « B » -
l’angle AOB
vaut 35,5° (à vérifier avec un rapporteur) |
|
|
Conclusion :pour construire un angle
on peut utiliser un rapport
trigonométrique. |
|
|
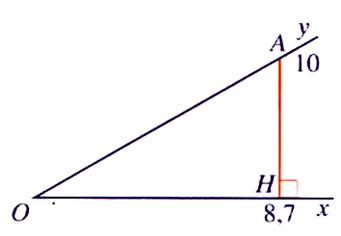
Mesure d’un angle « xOy »
donné sans le rapporteur . |
|
|
Procédure : -placer un point « A » sur [Oy) tel que OA = 10 cm ; -
tracer la projection
orthogonale de « A » sur
[Ox)
(image de « A » est « H ») -
mesurer la longueur
« OH » ( = 8,7 cm) -
on en déduit le cosinus
de l’angle « xOy » = -
A l’aide de la
calculatrice ou de la table : on obtient la
valeur de l’angle = 29,5° |
|
|
III)
Détermination d’une « longueur » appelé « hauteur » à
partir de calculs d’aires |
Rappel : cas d’ égalité des deux calculs
d’aire dans un triangle rectangle
|
ce qui donne après simplification : BC |
|
|||
|
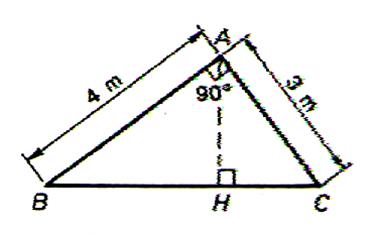
Application : Dans un triangle rectangle on nous donne :
BC = ? h = ? BA = 16 cm AC = 5 cm On veut connaître la longueur de l’hypoténuse et la longueur de la
hauteur. Résolution : il faut calculer
BC pour trouver la valeur de « h » ( voir Pythagore) |
Résolution : On sait que
dans un triangle rectangle BC |
|||
TRAVAUX AUTO FORMATIFS.
1°) Citez la
propriété de Pythagore et sa réciproque.
2°) Citez les rapports trigonométriques d’un angle
aigu
.3 °)
Propriétés : (énoncées à partir du sinus et du cosinus) ;
compléter les phrases :
a ) deux angles sont complémentaires
si :
b ) la tangente est égale au rapport du :
c ) « 1 » est égal à
quelle somme ?
|
Exercices : |
inter discipline : aire du triangle rectangle |
1°) Compléter ce tableau !
|
N° 1 |
N° 2 |
N° 3 |
N° 4 |
|
|
Grand coté « G » |
18 m |
|
40 |
|
|
Petit coté
« l » |
5 m |
|
|
35 |
|
Hypoténuse « L » |
Voir « Pythagore » |
45 cm |
50 |
65 |
|
Hauteur « H » |
12 cm |
|
|
|
|
Aire « A » |
|
|
|
|
|
Périmètre « P » |
|
|
|
|
|
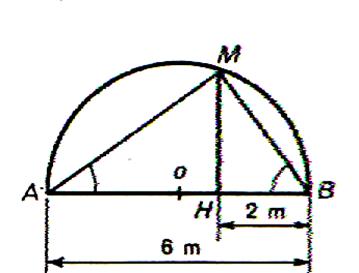
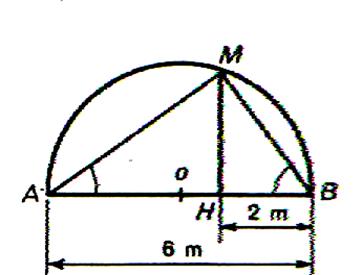
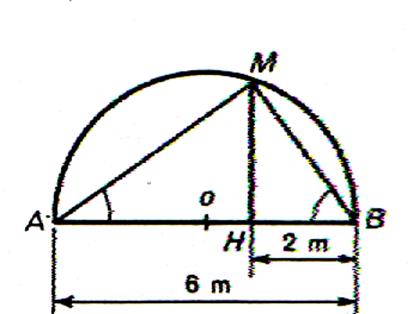
Enoncé : N°2 |
|
|
Calculer la longueur de la hauteur AH ( 1,2 m) |
|
Enoncé : N°3 |
|
|
Calculer en fonction de HA et HB ; (HM)2 |
|
|
Enoncé : N°4 |
|
|
Calculer HM |
|
|
Enoncé : N°5 |
|
|
Calculer en fonction de BH et BA ; (BM)2 |
|
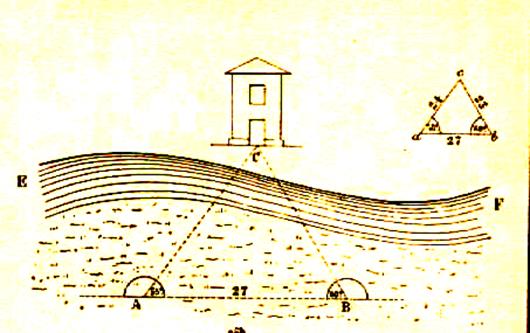
INTERDISCIPLINARITES
1°) La hauteur sous plafond est de 250 cm ;
les dimensions d’une armoire sont de 243 cm par 72 cm par 45 cm .
L’armoire est couchée , parviendra-t-on à la
« redresser » ?
2°) On achète une échelle de 10 m déployée ;
on l’adosse à un mur ; la législation impose que la distance entre le pied
de l’échelle et le mur doit être au moins égale à H / 4 .
Faire le croquis ; quelle est la
hauteur que peut atteindre le haut de l’ échelle ?
3° ) Une route à une pente
de 15% , quelle est la valeur de l’inclinaison en degré ?
4°) On
parle d’une pente de 100 % ; quelle est la valeur en degré de cette pente ?
|
5°)
calculer |
|
|
|
|
|
6°) |
|
|
|
|
|
7°) |
|
|
|
|
