|
Représentation des nombres trigonométriques |
|
|
Représentation graphique des nombres « sinus » et
cosinus » |
|
|
Pythagore et sa réciproque |
|
|
Le cercle trigonométrique |
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
|
DOSSIER : relation en sinus
et cosinus : cos2x + sin2x = 1
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
|
|
||||||||
|
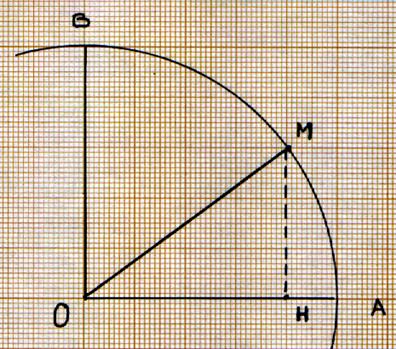
Le théorème de Pythagore , appliqué au
triangle OHM donne : OM2 = OH2 + HM2 M’ étant la
projection orthogonale de M on peut aussi écrire que : OM2 = OH2 + OM’2 Sachant
que
|
|
|||||||
|
OM ;
OH ;OM’ étant des nombres qui mesurent les
segments de même nom par rapport à une même unité . Si
l’on prend pour unité le rayon (valeur « 1 ») ,
cette relation devient : 12 = OH2 + OM’2 puisque (12 = 1 ) 1
2
= OH2 + OM’2 1 = cos2q +
sin 2q |
||||||||
En
plus :
|
Pré requis : les identités remarquables : A2 – B2
= ? |
|
|
|
Même pour un angle obtus , où le cosinus q serait négatif , cette relation reste exacte
puisque « cos q »ne figure
que par son carré. Soit la relation
« 1 = cos 2q + sin2 q » cette relation peut s’écrire :
cos2 q = 1
- sin 2q cos 2q = 12
- sin2 q soit : cos2
q
= ( 1+
sin q ) ( 1 - sin q ) ainsi cos q = la relation ainsi obtenue permet
de calculer « cos q » quand on
connaît « sin q » , ou inversement.
Mais , à une valeur donnée par « sin q »,
par exemple « sin q = 0,860 »
correspond à deux angles l’un aigu ,
l’autre obtus , admettant ce sinus : ils admettent deux cosinus opposés
, c’est ce qui explique le double signe . |
|
|
CONTROLE :
Dans un triangle rectangle :
montrez que 1 = cos2q + sin 2q
EVALUATION
Soit un triangle rectangle
, un angle = 30° ; avec votre calculatrice rechercher la valeur du
sinus et du cosinus . vérifier par le calcul
que : 1 = cos2q + sin 2q