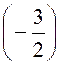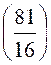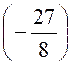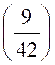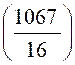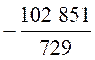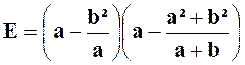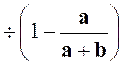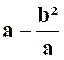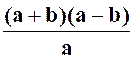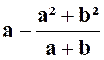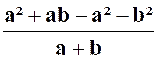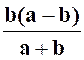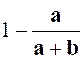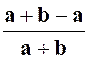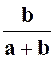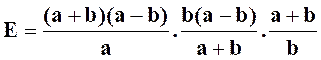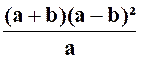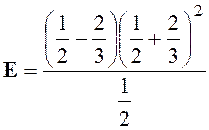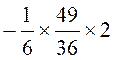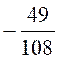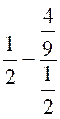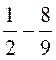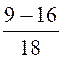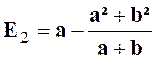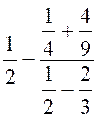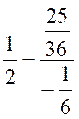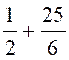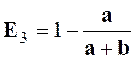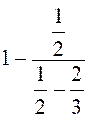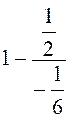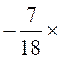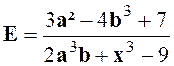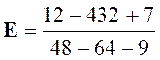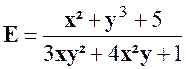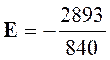COURS

Le calcul numérique joue un rôle très important dans les applications pratiques.

  Il faut donc s’habituer à calculer la « valeur numérique » d’une expression algébrique (dit aussi :expression littérale) lorsque l’on attribue aux lettres des valeurs numériques bien déterminées.

Pour mener à bien ces travaux cela nécessite « ordre » et « méthode »

Dans une majorité des cas on opérera en trois étapes :

1°) Remplacer purement e simplement des lettres par leur valeur. On doit se pénétrer que l’idée de remplacer, signifie « mettre à la place » ; cela sans opérer la moindre modification d’écriture, sauf l’enveloppement des nombres négatifs  entre parenthèse et parfois la mise en évidence du signe « multiplier par », là où il pouvait être sous entendu.

2°) Faire le calcul progressif sur les nombres affectés des différents signes d’opération.

3°) faire le calcul final.

( remarque : il faudra veiller  à respecter   l’ Usage des parenthèses )

Définition – On appelle « valeur numérique d’une expression algébrique » le nombre que l’on trouve lorsqu’on remplace les lettres par leurs valeurs et que l’on effectue les opérations indiquées , en respectant l’ordre de procédure des calculs .

·       Expressions algébriques :

 On appelle « expressions algébriques » ou « littérales » toute quantité écrite au moyen de la notation algébrique ; c'est-à-dire à l’aide de lettres et de signes  . 5ex. 3 a² , x-y ; n +1 .

·       Valeur numérique d’une expression.

La valeur numérique d’une expression algébrique est le nombre positif ou négatif qu’on obtient quand on remplace chaque lettre par le nombre particulier qu’elle représente et que l’on effectue les opérations indiquées dans l’expression.

Réduire en nombres une expression algébrique, c’est en calculer la valeur numérique.

En arithmétique ; lorsque l’on utilise des formules ( voir en calcul d’aire ; périmètre ….) ; on remplace des lettres par des nombres  , en vu de trouver une valeur numérique ; ce  calcul  est l’activité appelée : «  rechercher la valeur numérique d’une expression littérale » .

Remarques : Il y a les calculs avec des nombres   « abstraits » ( sans unité)  et des calculs avec des grandeurs ( nombres associés avec une unité ; appelés aussi « nombres concret » ).

Pour les nombres : il suffit de calculer en respectant les priorités.

Pour les grandeurs : il faut respecter les règles qui gèrent les unités ( convertir si nécessaire) , se référer au cours de sciences , au cas par cas .

Exemple 1 (avec des unités) – Calculer la valeur  numérique de l’expression suivante ( surface d’un trapèze ) , sachant que :

B = 12 m ; b = 8 m  et H = 3 m

S =

On obtient :

 S =  = 30 m²

Exemple II ( sans unités) : Calculer la valeur numérique  du binôme :

3a²b – 4ab

sachant que : a= 5 et b = 3

On obtient :*valeur  = 3 5² 3 - 4 5  3 = 165

Série 1  (niveau 6 et 5)

Exemple 1 -  Soit à indiquer la multiplication de la somme : 5 + 2 par le différence :  4 –3 .

Pour indiquer cette multiplication , on devra enfermer chaque facteur du produit entre deux signes appelés parenthèses .On écrira alors :

( 5 + 2 )  ( 4- 3)

Cela indique , qu’avant d’effectuer la multiplication , il faut effectuer les opérations qui sont indiquées dans les parenthèses .

On aura : ( 5 + 2 )  ( 4- 3)

Ou     7    1    =  7

Remarque – Le résultat ne serait point le même , si l’on se bornait à écrire  les deux facteurs  à la suite l’un de l’autre  , en les séparant par le signe de la multiplication .

On aurait alors :

5 + 2  4 – 3

Ce qui , en effectuant ,  étant donné  qu’on doit faire les multiplications avant les soustractions , donne :

5 + 8 – 3

et  13 – 3   = 10

Résultat faux  selon les donnés de l’exercice 1

Exemple II – Soit à indiquer la multiplication de  2a + b  + c  par  « a » 

Ici on ne peut effectuer la somme . On devra écrire :

(  2a + b  + c )  a

On a mis ainsi le polynôme  qui représente le multiplicande entre parenthèses .On peut encore simplifier l’écriture en supprimant le signe  ; car une valeur mise entre parenthèses , suivie d’un nombre ou d’une lettre  , indique une multiplication à effectuer  .

On aura alors : 

( 2a + b + c ) a   ou   a( 2a + b + c )

Remarque -  Si l’on n’avait pas mis le polynôme entre parenthèses , on aurait eu l’expression suivante :

2a + b + c  a

Ce qui donnerait : 2a + b + a c

Résultat dont la valeur n’est plus la même que lorsqu’on maintient les parenthèses .

Exemple III – Trouver la valeur numérique de l’expression suivante , en donnant aux lettres les valeurs suivantes :

     a =  4

     b= 3                      4 ( ab – c ) + 5 ( b c + a )

     c = 2

On aura :    4 ( 4  3 – 2 ) + 5 ( 3 2 + 4 ) =

                                       4  10 + 5  10 =

                                                    40 + 50 = 90

Exemple IV – Calculer la valeur numérique de l’expression précédente , en gardant les mêmes valeurs aux lettres et en supprimant les parenthèses .

On aura à écrire : 

                      4  4  3 – 2   + 5  3 2 + 4     =

ou                                       40   +      34             =  80

On constate que le résultat est loin d’être le même , mais il est exact , s’il n’existait pas de parenthèses .

Remarque . – Nous reparlerons des parenthèses plus loin , dans la mise en facteurs communs , mais  , dès maintenant , on peut se rendre compte  de leur importance  et de la nécessité  d’y faire attention dans les calculs .

Série  n°2 :    d’exemples niveau 4 :

Exercice 1 :

Calculer la valeur numérique de polynôme :  P ( x ) =  - 8 x ⁹  + 3 x ⁷ + 11 x ⁴ – 13 x + 4                          ; pour «  x = - 2 »  

Solution :

1°) remplacement de « x » par ( - 2 )

  P ( - 2 ) =   - 8 ( - 2 ) ⁹  + 3 ( - 2 ) ⁷ + 11 ( - 2 ) ⁴ – 13 ( - 2 ) + 4    

2°) Calcul progressif . Il est recommandé de commencer par le calcul des puissances de ( - 2 ) :

( - 2 )²  = (+4) ; ( - 2 )³ = ( - 8 ) ; ( - 2 )⁴ = ( + 16 ) ; ( - 2 )⁵ = ( - 32 ) ;  ( - 2 )⁶ = ( + 64 ) ; ( - 2 )⁷ =  ( - 128 ) ; ( - 2 )⁸ = ( + 256 ) ; ( - 2 )⁹ =  ( - 512 )

Dés lors :  P ( - 2 ) =   - 8 ( - 512 )    + 3 ( - 128 ) + 11 ( + 16 ) – 13 ( - 2 ) + 4

                                 Calcul final : 

:  P ( - 2 ) = 4 096 – 384 + 176 + 26 + 4 =  3 918

Exercice 2 :

Calculer la valeur du polynôme   P ( x ) =  5  x ⁴  - 3 x ³ + 7 x² - 9 x + 2       pour  « x =  »

P  =  5  ⁴  - 3  ³ + 7 ² - 9  + 2 

P  =  5  ⁴  - 3  ³ + 7 ² - 9  + 2 

Réponse : P  =

Exercice 3 :

P ( x ) =  - 2 x ⁶  + 4 x ⁵  - 7 x² + 11x – 9    pour  «  x =   »

Réponse : P ( ) = 

Série n °3   :

Lorsque l’on doit rechercher la valeur numérique d’une expression algébrique , il arrive que l’on doit travailler sur des expression plus ou moins compliquées. Donc , avant tout calcul numérique , il conviendra de la transformer pour lui donner sa forme la plus simple possible. C’est sur cette forme « définitive » que l’on fera le calcul. !!!!

Exercice 4 :

Calculer la valeur numérique de l’expression :       pour «  a =  » pour  « b= »

Solution : nous transformons l’expression d’après les principes exposés dans le cours «  expressions algébriques quelconques , mais rationnelles. »

  =      ;     =   =

 =    = 

Donc :    = 

La valeur numérique est alors :    =    = 

Une excellente vérification consiste à faire le calcul sur la forme originelle. C’est très éducatif :

 =    =          =   =   =

  =   =    =    = 

 =    =   = 1 + 3  = 4

Dés lors :   E  =     =   =  -

Exercice  5  : Calculer la valeur numérique de l’expression :

             ; pour  «  a = - 2 »   ; «  b = - 3 » et « x = - 4 )

Indications : l’expression « E » ne peut pas être simplifiée.                      ; Réponse :   E  =

Exercice 6  : Calculer la valeur numérique de l’expression :

           ; pour   «  x =  »   ;  «  y =  »   ; Réponse :