|
Auteur :
WARME R.
INFORMATIONS sur
|
||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
|
Année scolaire : ……………………… |
Dossier
pris le : ……/………/……… |
Validation
de la formation : O -
N Le : …………………………………….. Nom
du formateur : …………………… |
|
ETABLISSEMENT :
………………………………………….. |
||
iNous avons déjà recherché un résultat en remplaçant
des lettres par des nombres .lors de
la leçon sur les « nombres décimaux relatifs @ ( voir
les derniers exercices de l’évaluation )».
Il
est souhaitable de reprendre ces calculs
et pour les mettre en lien ce qui
a té fait avec ce cours .La leçon « sur la recherche d’une valeur numérique d’une expression littérale »
est la suite des calculs avec des
nombres relatifs .
Le
but de la leçon « valeur numérique
d’une expression littérale » étant d ’ utiliser des
« formules » qui sont
utilisées le cadre professionnel.
Dans
le programme il n’est pas prévu de traiter « normalement » la leçon
sur les priorités dans les calculs .
Pourtant
il faut connaître l ’ordre dans lequel on effectuera les opérations ;: par quelle opération
commence t - on ? et par quelle termine - t - on ? si il y a ( en partie ou tout )
des additions ,soustractions , multiplications ,divisions et puissances
voir racine dans une chaîne d’opérations .
|
cliquer
ici : Les
chaînes d’opérations , dit
aussi : opérations combinées et les priorités
de calculs . |
|
|
LECON |
|
|
RECHERCHE DE LA VALEUR NUMERIQUE D’ UNE EXPRESSION
LITTERALE . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
COURS
iEn arithmétique , lorsque
l’on utilise des formules ( voir :calcul d’aire ;
périmètre ….) ; on remplace des lettres par des nombres ( grandeurs) , en
vu de trouver une valeur numérique ; ce
calcul est une activité appelée :
« rechercher la valeur numérique d’une expression littérale » .
|
Définition : Pour calculer la valeur
numérique d’une expression littérale , on
remplace les lettres par les valeurs qui lui sont
attribuées (données) . |
Il en est de même si l’on calcule
la valeur numérique d’une expression
algébrique .
Exemples de formules (
expressions littérales ) couramment usitées
|
Cas de calculs |
Formules Sur le C D vous
avez une foule de situations problèmes
traitant chaque cas |
Pour plus d’informations |
|
Aire du
carré |
A = c² |
|
|
Périmètre
du carré . |
P =4c |
|
|
Longueur
d’une circonférence. |
P = 2 p R |
|
|
Aire
d’un disque. |
A = p R
² avec (p » 3,14 ) |
|
|
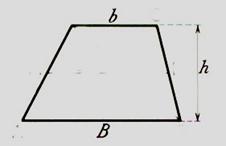
Aire du
trapèze. |
|
|
|
Périmètre du rectangle. |
P = 2 (
L + l ) |
|
|
Aire du rectangle . |
A = L |
|
|
Aire du triangle |
A = |
Un calcul numérique comporte plusieurs étapes qui, à chaque
fois sont :
-
soit changer l’écriture d’un
nombre.
Exemple : ![]() =
= ![]() = 3,5
= 3,5
-
soit effectuer une série de transformations grâce à une règle (ou une procédure)
Exemple : ![]() +
+ ![]() =
= ![]() =
=
![]()
Préambule : Pour
pouvoir effectuer un calcul ou une série de calculs , en vu de trouver un
nombre (appelé : résultat ) , il faut avant tout savoir le lire et donc de connaître les conventions d’écritures
et les priorités opératoires .
En calcul numérique :
· On n’écrit jamais deux signes qui se suivent
sans parenthèses .
on n’écrit
pas 3 ´ - 4 mais
on écrit 3 ´ ( - 4 )
· Au lieu
d’écrire 3 ´ 3 , on écrit 3² ; et 3´ 3´ 3
s’écrit 33
· Le trait de fraction signifie la division du
numérateur par le dénominateur et tout se passe comme si le numérateur et le
dénominateur étaient entre parenthèses.
Ainsi :
* ![]() s’écrit
5 ÷ 2 + 3 = ; qui s’écrit
aussi ( 5 ÷ 2 ) + 3
= 5,5
s’écrit
5 ÷ 2 + 3 = ; qui s’écrit
aussi ( 5 ÷ 2 ) + 3
= 5,5
* et ![]() s’écrit
( 5 +3 ) ÷ 2 = ; soit
(8 ) ÷ ( 2 ) = 4
s’écrit
( 5 +3 ) ÷ 2 = ; soit
(8 ) ÷ ( 2 ) = 4
|
I.2.
Principales règles de transformations de
l’écriture des nombres |
Il est souvent très utile de transformer les écriture des
nombres et de les remplacer par une valeur numérique. Nous retiendrons les
transformations suivantes :
A) :
@ i 3² signifie 3 ´ 3 ( =
9 ); comme 33 signifie
3´ 3´ 3 ( = 27)
B ) : @ i Le
trait de fraction signifie une division : ![]() = 2,5
= 2,5
C ) : @ i « simplifier » ; « rendre irréductible » et
« réduire au même dénominateur »
![]() =
= ![]()
Les nombres « k » et « b » sont des
nombres non nuls . cette écriture permet
de simplifier une fraction
ou de réduire deux
fractions aux mêmes
dénominateurs.
- Simplifier directement les fractions suivantes :
|
Soit la
fraction : |
On peut
diviser le numérateur et le dénominateur par : |
On peut
ainsi remplacer : |
|
|
« 2 » pour
simplifier ou
« 4 » pour
rendre irréductible . |
Par
4 / 6 ou 2 / 3 |
-
C 1
) Réduire au même dénominateur 2 fractions :
![]() résultat : le dénominateur commun est
« 40 » ;
résultat : le dénominateur commun est
« 40 » ;
les deux fractions équivalentes aux fractions 7 / 10
et 3/ 4 sont 28 / 40 et 30
/ 40
-
C 2
) Réduire au même dénominateur 3
fractions :
![]() résultat : le
dénominateur commun est
« 60 » ;
résultat : le
dénominateur commun est
« 60 » ;
les
trois fractions équivalentes aux fractions 7 / 10
et 3/ 4 et 18/30 sont 42 / 60 et 45
/ 60 et 36 / 60
D) : @ i L’écriture décimale
et les puissances de dix :
exemples :
b) 0,45 = ![]() = 45 ´ 10 -2
= 45 ´ 10 -2
E ) :@i L’écriture
décimale et les pourcentages :
exemple : 0,145 = ![]() = 14,5
%
= 14,5
%
si la fraction n’est pas
« décimale » ,il faudra :
E 1 ) : @ i- ou
rendre la fraction irréductible .et continuer les calculs avec cette fraction.
E 2 ) : @ i- ou effectuer la division et remplacer la fraction par un nombre décimal « arrondi » à 0, ? ? ?1 prés . On remplace le « ? » par un ou plusieurs« 0 »
F ) : @ i L’écriture ![]() par la
valeur de la racine
par la
valeur de la racine
exemples : on
remplacera ![]() par 3 ;
par 3 ;
et ![]() par une valeur approchée » 3,162 )
par une valeur approchée » 3,162 )
|
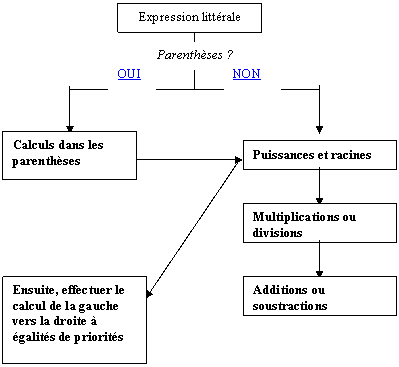
I.3. Priorités opératoires : Recherche d’un résultat numérique . |
le
résultat peut être recherché soit à
partir d’une formule ou d’une chaîne d’opérations possédant ou non des
parenthèses.
Organigramme concernant l’ordre chronologique des
calculs :
¶ Résultat
numérique recherché à
partir d’un énoncé et d’une formule donnée
Si les calculs s’effectuent
à partir d’une formule donnée :
+Le calcul est direct :
Il n’y a que des
nombres séparés par des signes opératoires dans le deuxième membre , le résultat
s’obtient directement ;on remplace chaque
lettre par leur valeur numérique ,ensuite on effectue les calculs .
Exemple : Calcul d’aire du trapèze (à l’aide de la
formule : ![]() )
)
Application : Un trapèze a les dimensions suivantes :
B = 12,6 cm ; b = 7,4 cm ; h = 6,8 cm.
Calcul de son aire . A = ![]() =
68 cm2
=
68 cm2
+Le calcul est
indirect :
L’expérience et les connaissances en algèbre sont
nécessaires ! ! ! ! ! !
Il y a des nombres
dans les deux membres de l’égalité , il y a une lettre dans un des membres ,
qu’il faut isoler . C’est alors un problème d’algèbre : il faut faire
l’inventaire des données numériques , on identifie ce que l’on cherche , on transforme l’égalité
pour isoler l’inconnue , on fait le calcul .
Exemple
: Trouver la hauteur du trapèze qui à une aire de 50 m2 et
dont les bases mesurent 12,6 m et
7,4 m .
Soit la
formule : ![]() ;
on remplace les lettres par les valeurs données :
;
on remplace les lettres par les valeurs données : ![]()
On transforme pour obtenir : h= ![]() =
=![]() =
5 m
=
5 m
( info @ + :voir le cours sur « résoudre un
problème du premier degré »)
· Résultat
numérique à rechercher à partir
d’une chaîne d’opérations :
Exemple de calculs à
effectuer dans une chaîne d’opérations
L’expression contient
des additions, soustractions
,multiplications ,divisions (ou fractions….) , des puissances , des racines:
Exemple 9,2 - 42 ![]() 7
+ 2,7
7
+ 2,7 ![]() (-6)2 +
(-6)2 + ![]() -
- ![]() =
=
|
Procédure |
Exemple |
|
|
1ereEtape |
Calculer
la racine au préalable faire le calcul
sous la racine au cas où….. |
9,2 - 42 |
|
2emeEtape |
Calculer
les puissances |
9,2 - 16
|
|
3emeEtape |
Calculer
les divisions |
9,2 - 16 |
|
4emeEtape |
Calculer
les multiplications |
9,2 - 112 +
(+ 97,2 ) + 5 -
20 |
|
5emeEtape |
Transformer
l’expression algébrique en somme algébrique |
(+9,2)+( - 112) + (+ 97,2 ) + (+ 5) + ( - 20) |
|
6emeEtape |
Calculer
la somme des nombres positifs |
(+9,2)+ (+
97,2 ) + (+ 5) = (+(9,2+97,2+5)= (+
111,4) |
|
7emeEtape |
Calculer
la somme des nombres négatifs |
( - 112) + (
- 20) =( - (112+20)) = (-132) |
|
8emeEtape |
Calculer
la somme des nombres de signe contraire |
(+ 111,4)+ (-132)
= ( - (132- 111,4)) = (-20,6) |
|
9emeEtape |
Rendre
compte |
9,2 - 42 |
ACTIVITES : Calculer (CORRIGE : CLIQUER ICI )
1°) 3 + 5,6 + 8 =
2° ) - 5 - 6,3 -7,2 =
3° ) -8,3 + 5 - 9 - 13,5 + 7,7 =
4°) 15,3 - 4 ![]() 5,3
+ 7
5,3
+ 7![]() 3
=
3
=
5°) 3, 5 - 9 : 2 + 4![]() 9
=
9
=
6°) -8.4
+ 11 +![]()
![]() 1,2
=
1,2
=
7 °) 3, 52- 9 : 2 + 4![]() 92
=
92
=
8 ° ) -8,42 + 11 +
(![]() )
2
)
2![]() 1,2 =
1,2 =
9°) 9,2
- 42 ![]() 7 + 2,7
7 + 2,7 ![]() (-6)2 +
(-6)2 + ![]() -
- ![]() =
=
|
II.
NOTIONS sur le CALCUL ALGEBRIQUE et exemple de résolution de problèmes à traiter
avec l ’ algèbre . |
i Les objectifs
de base en algèbre qu’il faudra atteindre en fin de niveau V
sont :
- savoir effectuer des calculs qui comportent des
variables ou des inconnues ( notées généralement « x » et
« y ») ; savoir développer et factoriser des expressions ,
- savoir mettre un problème en équation et
- savoir
résoudre des équations ( et système) du premier degré .
Ce cours a pour
but de vous familiariser au vocabulaire qui sera
utilisé dans les objectifs cités ci - dessus .
i Dans les
expressions algébriques le signe
« multiplié » n’est jamais
représenté.
On n’écrit pas les signes ´, sauf entre deux nombres
( pour ne pas confondre entre 24
et 2 ´ 4 )
Exemples :
|
Formule |
En
omettant les signes ´ |
L’expression
se lit : |
|
2 ´ p ´ R |
2p R |
2 fois
pi fois R |
|
3´x |
3x |
3 fois
ixe |
|
a´b |
ab |
a fois b |
|
a´b´c |
abc |
a fois b fois c |
|
3´ |
3 |
3 fois racine carré de 18 |
|
2 ´ x ´ ( 1
- x ) |
2 x (
1 - x ) |
2 fois x
facteur de 1-x |
|
3 ´ ( 2´ x + 1) |
3 ( 2x +
1) |
3
facteur de 2 ixe plus un |
|
x ´ ( 2´x +2 )
|
x ( 2x +2 ) |
ixe
facteur de 2ixe plus 2 |
|
(2´x +1)´(3´x + 2) |
(2x+1) (3x+2) |
2ixe
plus un entre parenthèses facteur
de 3 ixe plus 2. |
iremarque :
les groupes de mots
« fois entre
parenthèses » et « facteur de » ont la même signification .
êATTENTION au risque d’erreur : ne pas confondre ce qui est dit et de ce
qui est écrit :
Exemple 1 : a +b² est différent de l’écriture ( a + b ) ²
3 + 5
² = 3 + 25 = 28
¹ (3+5)² = 64
Exemple 2 : a - b² est différent de l’écriture ( a -
b ) ² ;
3 -
5² =
3 - 25 =
- 23 ¹ ( 3
-5 )² = 4
A retenir :
Quand on
multiplie un nombre par une lettre ou une parenthèse, on n’écrit pas le signe ´