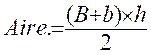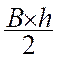Lecture : classe de 3^ème
CAP	DOSSIER : EQUATION du premier degré / Objectif cours 33

Pré requis:

Lecture : l’algèbre

Voir les calculs : les égalités

Expression algébrique et somme algébrique .( définitions)

Les conventions d’écriture

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent : 1°) les conventions d’écritures 2°) les priorités de calcul 3°) le calcul numérique ( niveau V) 4°) L’emploi des lettres en mathématiques

Objectif suivant 1°)Equation du 1er degré à 1 inconnue 2°) les fonctions : calculs algébriques pré requis . 3°) valeurs numériques d’une expression algébrique. 4°) valeurs numériques d’une expression littérale . 5°) résumé sur le Calcul littéral (niveau lycée)

1°) Retour vers les cours d’algèbre 2°) devoir C.C.

DOSSIER :

Les Ecritures littérales

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité Devoir 2°)Sciences : utilisation des formules 3°) travaux niveau IV

Corrigé Contrôle

Corrigé évaluation

Calcul 6e

COURS

Origine :

Viète

Viète François : ( né en 1540 à Fontenay – le – Comte) :

Il vécut durant les guerres de religions , et il peut être considéré comme étant le père des écritures mathématiques modernes .

Après avoir su déchiffré les messages secrets que s’expédiaient les états espagnols éloignés et dispersés . Il invente des notations et des écritures mathématiques qu’il rassemble dans un livre intitulé «  L’algèbre nouvelle » , où il montre le formidable intérêt que l’on a en mathématique à calculer sur des lettres plutôt que sur des valeurs et exemples numériques .

Exemples :

Il décide :

De représenter par les lettres de l’alphabet A ; B ; C ;…. Toutes les grandeurs intervenant dans les calculs , qu’elles soient connues ou inconnues.

De réserver pour les grandeurs connues les consonnes B ; C ; D ; … et pour les inconnues les voyelles A ; E ; I ; O ; …

D’indiquer par la notation actuelle l’addition « + » ; la différence « -»  le quotient

puis Descartes :

c’est Descartes qui améliora encore les notations de Viète . A lui , nous devons les « x ; y ; z » pour les inconnues , les « a ; b ; c ; … » pour les autres quantités du calcul littéral .

«  cette espèce d’arithmétique qu’on appelle « algèbre » , faite pour exécuter sur des lettres ce que les anciens faisaient sur des nombres ou des figures soulage l’imagination ; elle aide à se dégager des difficultés qui sont cachées dans la confusion des nombres et des figures et possède désormais cette clarté et cette facilité suprême qui doit se trouver dans la vraie mathématique .…… L’algèbre ramène de l’étude particulière de l’arithmétique et de la géométrie à une générale des mathématiques .

Initiation aux écritures littérales :

Tout mathématicien se doit d’exceller dans l’art d’être concis , c’est à dire de savoir en un minimum de phrases , de mots , d’égalités , bref de choses écrites , exprimer parfaitement et en totalité une question posée et sa réponse.

Le problème suivant :

Trouver la mesure du côté d’un carré dont le périmètre est de 36 mètres , se traduit , en désignant par la lettre « a » la mesure cherchée , et en se référant à la formule du périmètre du carré ( 4 lg. côté) , par l’égalité : 4 a = 36 ( en mètre).

L’écriture 4 a ( ou plus simplement 4a ) est appelée une écriture littérale ,

La lettre « a » remplaçant la mesure du côté du carré est elle – même une écriture littérale .

Toutes les formules des périmètres ( L + l ) 2 pour le rectangle , 2pR pour le cercle ou les aires L l pour le rectangle ; a a ou ( a²) pour le carré , p R² pour le disque sont des écritures littérales .

( Littérale : du latin littera » , lettre )

Voir les applications en sciences .

Exemples de formules ( expressions littérales ) couramment usitées :

Aire du carré	A = c²	Info plus !
Périmètre du carré .	P =4c	Info plus !
Longueur d’une circonférence.	P = 2pR	Info plus !
Aire d’un disque.	A = pR² avec (p » 3,14 )	Info plus !
Aire du trapèze.		Info plus !
Périmètre du rectangle.	P = 2 ( L + l )	Info plus !
Aire du rectangle .	A = L l	Info plus !
Aire du triangle	A =	Info plus !

CONTROLE:

Qu’ appelle-t-on «  écriture littérale » ?

EVALUATION:

c)