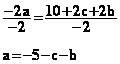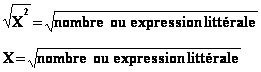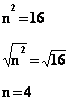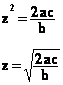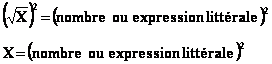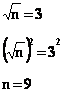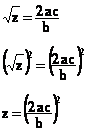Lecture : L’écriture littérale
CALCUL LITTERAL
L’objectif
de ce chapitre est de revoir tous les mécanismes opératoires et les propriétés
des opérations, d’aborder la notion de variable, de gérer une formule
littérale.
RAPPELS DE CALCULS
NUMERIQUES
Les ensembles
de nombres en mathématiques sont les suivants :
N : ensemble des entiers
naturels : 0 ; 1 ; 2 ; ......etc...........
Z : ensemble des entiers
relatifs : ......-2 ; -1 ; 0 ; 1 ; 2 ; 3.......etc.....
D : ensemble des nombres
décimaux : -1,8 ; 2,7 ; ............etc....
Q : ensemble des nombres
rationnels : on peut les écrire comme le rapport de deux nombres entiers
relatifs : 2/3 ; -5/6 .........
R : Ensemble des nombres
réels
Avec le développement de la géométrie est apparu le
besoin de créer de nouveaux nombres. Ainsi, la longueur de la diagonale d’un
carré dont le côté mesure une unité ne peut s’exprimer à l’aide d’une fraction.
Cette longueur est égale à la racine carrée de 2 de symbole 
,Multipliée par elle-même, cette valeur vaut 2. De
même, le quotient de la circonférence d’un cercle par son diamètre n’est pas un
nombre rationnel, mais vaut pi = 3,1415... Ces nombres sont dits irrationnels.
La réunion de l’ensemble des
nombres rationnels et de l’ensemble des irrationnels constitue l’ensemble des
nombres réels.
Un
même nombre peut avoir plusieurs écriture
possibles :
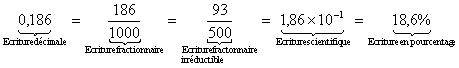
Calculs
avec des nombres réels
Pour
pouvoir faire du calcul littéral, il est important de savoir transformer
correctement une suite d’addition et de soustraction en somme algébrique :
Exemple : 
Plusieurs
règles sont à connaître avant de se lancer dans le calcul, en voici quelques
rappels :
1.
Les écritures équivalentes de fractions :
2.
Règles de calculs sur les fractions :
a.
Pour additionner ou soustraire des fractions, il faut
les réduire au même dénominateur
b.
Pour multiplier des fractions entre elles, on
multiplie les numérateurs entre eux (les nombres au dessus du trait de
fraction) et les dénominateurs entre eux.
c.
Pour diviser une fraction par un nombre on la
multiplie par son inverse
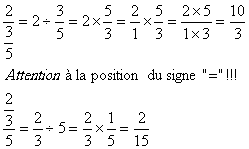
D’une
manière générale diviser par un nombre c’est multiplier
par son inverse.
L’inverse de 
est 
,de plus 
1.
Pour soustraire un nombre on ajoute son opposé.
On transforme la soustraction en
somme algébrique.
Revenons
à l’exemple :
Passage
aux écritures équivalentes des fractions :
Transformation
des soustractions en sommes algébriques :
Etant
donné qu’il y a des fractions, il faut tout réduire au même dénominateur :
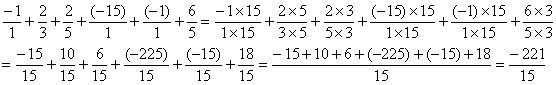
La
fraction doit être irréductible.
2.
Rappel sur les racines carrées a et b sont
positifs :
a.
b.
c.
3.
Les exposants :
4.
Les priorités opératoires classées dans l’ordre
décroissant de priorité
a.
Puissances et racines carrées
b.
Calculs entre parenthèses
c.
Multiplication et division
d.
Addition et soustraction
FExercices
a.
Effectuer à la main les calculs suivants et contrôlez
à la calculatrice :
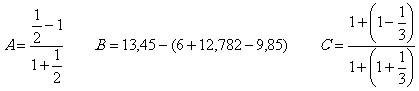
b. Mettre les
nombres suivants sous la forme d’une puissance d’un même nombre :
c.
Donner l’écriture décimale et l’écriture scientifique
des nombres suivants :
d.
Donner une écriture plus simple des nombres
suivants :
LES EGALITES
REMARQUABLES
Ce
sont des égalités vraies quelques soient les valeurs données aux nombres a et
b, les trois égalités les plus utilisées sont :
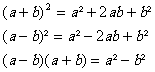
Développer
une de ces égalités consiste à écrire pour la première par exemple :
Factoriser
une de ces égalités consiste à écrire pour la seconde par exemple :
A la place
de a et b il peut y avoir n’importe quel autre lettre ou forme littérale, mais
pour développer ou factoriser, il faut bien identifier ce qui correspond à a et
b.
Exemples
F
Comment développer (x-7)² ?
(x-7)²
correspond à (a-b)² avec a=x
et b=7 ainsi :
(x-7)²
= x² - 2 ×x×7 + 7 ² = x² - 14 x + 49
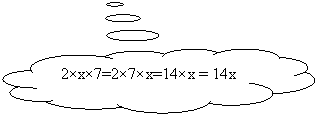
F
Comment factoriser une égalité remarquable ?
Il
faut identifier à quel développement elle correspond :
§
A²-14A+49 = A² - 2 × 7 × A + 7 ² =(A-7)²
§
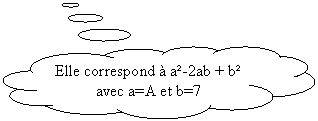
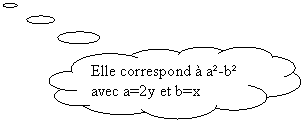4y²-x² = (2y)²
- x ² = (2y-x)(2y+x)
F
Exercices
§
Développer les expressions suivantes :
a)
(x-2)² b) (2y-1)(2y+1) c) (2t-1)² d) (x-y)² e) (2a-3b)(2a+3b)
§
Factoriser les expressions suivantes :
a)
16x²+8x+1 b) 4-20y+25y² c)4x²-1 d) 28x²-7 e)5+10y
+ (1+2y)²
DEVELOPPER, REDUIRE ET
ORDONNER UNE EXPRESSION LITTERALE
Dans le cas où le développement fait apparaître des
termes de même nature, il faut les regrouper ( on dit
réduire les termes de même nature) :
Exemple
2(x-7)² -
3x² + 15x(x-7)(x+7)
= 2(x²-14x+49)
– 3x² + 15x(x²-49) Ü Développement des identités remarquables
= 2x² + 2×(-14x) + 2×49 – 3x² + 15x×x² + 15x×(-49) Ü Distribution des facteurs
= 2x²+(-28x)+98-3x²+15x3 + (-735x) Ü Calculs des produits
= 2x²+(-28x)+98+(-3x²)+15x3
+ (-735x) Ü Transformation en somme algébrique
= 2x² + (-3x²) + (-28x)+(-735x) + 15x3 + 98 Ü Regroupement des termes de même nature
= -x² + (-763x) + 15x3
+ 98 Ü Réduction
=
15x3 + (-x²) + (-763x) + 98 Ü ordonnément des termes suivant les puissances croissantes de x
=
15x3 – x² - 763x + 98 Ü Simplification d’écriture.
NB :
15x3 – x² - 763x + 98 est un polynôme de la variable x, le degré de
ce polynôme est 3.
Pour
réussir en calcul littéral, il faut simplement faire beaucoup d’exercices, les
voici :
FExercices
§ Calculer les
expressions littérales suivantes :
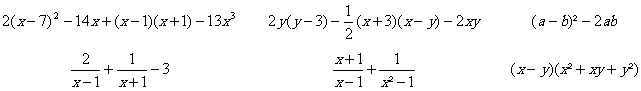
§ Les lettres a, b
et x désignent des réels, montrer que :
§ On donne le
polynôme P(x)=-x3+5x²+4x-2, déterminer les réels a,b
et c pour que P(x) puisse s’écrire :
P(x)=(x+1)(ax²+bx+c)
Simplifier
ensuite la fraction suivante : 
§ Effectuer le
calcul :
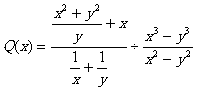
CALCULER LA VALEUR
NUMERIQUE D’UNE EXPRESSION LITTERALE
Pour calculer la valeur numérique d’une expression
littérale, il suffit de donner une valeur à chaque lettre intervenant dans la
formule, on dit que l’on fait une substitution.
On substitue à la lettre sa valeur.
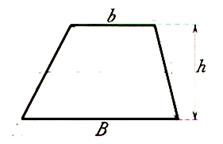
Exemple de calcul
|
On donne les dimensions du trapèze B = 8 ; b =
5 et h = 4 ( l’unité de longueur est le cm) On veut connaître son aire . L’expression littérale donnant l’aire d’un trapèze est : A = |
|
|
Donc A = On calcule dans les parenthèses :A
= On calcule (13)4 = 4 ( 13) =
4 A = On divise : 52 :2 A = 26 On conclue : l’aire
du trapèze est de 26 cm² |
|
13
F Exercices
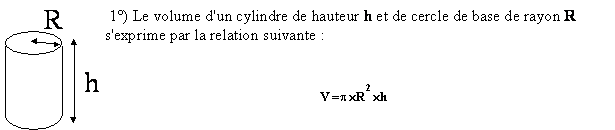
Calculer le volume
V (arrondi à 0,1 près) du cylindre en m3 pour les différentes
valeurs de R et h suivantes
:
· R = 0,2 m h = 0,5 m V =
· R = 1,5 m h = 1,5 m V =
2°)
La formule ci-dessus établie par Lorentz permet de calculer la masse m idéale(exprimée
en Kg) d'un individu par rapport à
sa taille( exprimée en cm) :
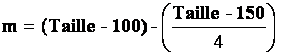
a) Calculer la "masse idéale" d'individus
dont les tailles sont les suivantes :
1,50
m ; 1,75 m ; 1,80 m ; 1,95 m ; 1,65 m
b) Calculez votre propre "masse idéale".
3°)
On donne B(x)=x3-x²-5x+6
a)Calculer B(2)
b) Déterminer la valeur de b pour que B(x) puisse
s’écrire (x-2)(x²+bx-3)
4°)
On donne l’expression C(x)=2x²-40x+500
a)
Calculer C(0) ;
C(5) ; C(10) ; C(15) ; C(20) ; C(25).
b)
Le coût de production d’un article est donné par la
relation :
C(q)=2q²-40q+500
Le prix de vente de cet article est
donné par la relation :
P(q)=10q+300
Compléter le tableau suivant :
|
q |
0 |
5 |
10 |
15 |
20 |
25 |
|
C(q) |
|
|
|
|
|
|
|
P(q) |
|
|
|
|
|
|
Sur quel intervalle la production
est-elle rentable ?
TRANSFORMATIONS D'EXPRESSIONS
LITTERALES
Dans un problème ou un exercice, la formule donnée
n'est pas forcément sous la forme qui permet de faire le calcul directement, il
faut d'abord la transformer pour calculer ce qui est demandé.
À Transformations simples
Exemple : La loi d'OHM est une formule permettant de calculer la tension U(en Volt) aux bornes d'un résistor en fonction de la valeur
de sa résistance R(en Ohm) et de la valeur
de l'intensité I( en Ampère) du courant qui le traverse.
Cette formule est : U = RI. On demande de calculer I
pour U = 10 V et R = 250 W.
La méthode consiste à considérer I comme inconnue et
de transformer la formule en appliquant la règle de résolution des équations du
premier degré à une inconnue : Il faut isoler l'inconnue dans
un des membres de l'équation en effectuant les opérations nécessaires sur les deux
membres de l'équation.
(a>0)
