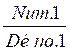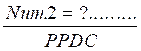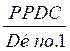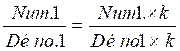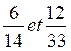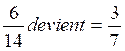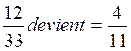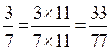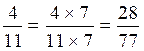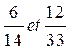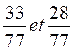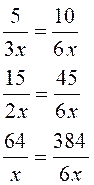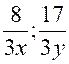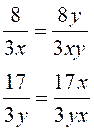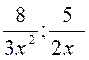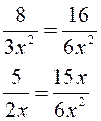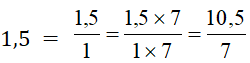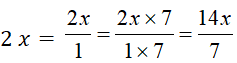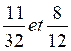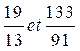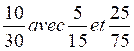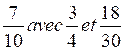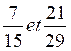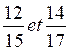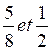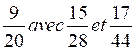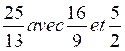LES FRACTIONS :
TRANSFORMATIONS
Sciences : réduction au même
dénominateur
|
|
Rappels
|
Pré requis:
|
|
|
|
Calcul du PPCM |
|
|
Recherche du
dénominateur commun (Plus Petit
Dénominateur Commun ) |
|
|
|
|
|
Transformer une
fraction en une fraction équivalente de
dénominateur donné |
ENVIRONNEMENT du
dossier :
|
Objectif précédent : Réduire
deux fractions au même dénominateur |
Objectif suivant : |
DOSSIER
: REDUIRE aux mêmes dénominateurs des fractions.
|
|
I
)Rappel dont la Procédure pour transformer une fraction en fraction équivalente dont on à
déterminer par le calcul le dénominateur : |
|
|
|
II ) Procédure
permettant de réduire deux fractions au même dénominateur. |
|
|
|
III
) APPLICATION
en algèbre: |
|
|
COURS |
Interdisciplinarité |
|
|
|
Commentaire: lorsque l’on veut
additionner ou soustraire deux fractions de dénominateur différent il faut
impérativement passer par ces calculs; lorsque les deux fractions sont réduit au même dénominateur on applique la règle concernant l’addition ou
la soustraction de deux fraction de même dénominateur. Pré requis: calcul du Plus Petit Commun Multiple (ou Plus petit multiple commun)
appelé "PPDC" PPDC L Plus Petit
Dénominateur Commun ) Lorsque l 'on aborde les fractions en vue de les additionner ou
soustraire) |
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
Par définition : Réduire deux fractions au même
dénominateur. ,C’est transformer deux fractions de
dénominateur différent en fractions équivalentes de même dénominateur. A ) Intérêt de savoir-faire cette
transformation : On ne peut pas additionner ou soustraire deux fractions de
dénominateur différent. Pour contourner la
difficulté on doit transformer les fractions . Les
nouvelles fractions seront des fractions équivalentes qui devront avoir le même dénominateur Ce qui rendra ensuite
l’opération (addition ou soustraction) possible b)Pouvoir classer ,ordonner dans un ordre croissant ou
décroissant des fractions. RAPPELS Procédure qui permet de transformer une fraction donnée en (une nouvelle ) fraction équivalente dont le nouveau
dénominateur est imposé ou obtenu en calculant un PPDC : Pour
transformer une fraction en une fraction de même valeur (
équivalente) il y deux
possibilités soit de calculer le coefficient multiplicateur permettant de
passer d’une fraction à une autre fraction équivalente ou soit de passer par
le produit en croix en posant « x » au numérateur de la
deuxième fraction.) · Procédure pour transformer une
fraction en fraction équivalente dont
on à déterminer par le calcul le dénominateur : (solution proposée: calcul du
coefficient multiplicateur « k ») a) On pose
l’égalité de la fraction donnée (
b)
Le PPDC est un multiple du Dénominateur de la première fraction
(Déno.1); on divise le PPDC par Déno1
on trouve un nombre entier (appelé : k)
c) On calcule la valeur de Num.2: Num 2 = Num. d) Rendre compte: pour chaque
fraction : fin du rappel. |
|
||||
|
|
II ) Procédure permettant
de réduire deux fractions au même dénominateur. |
|
||||
|
|
Exemple d’énoncé :soit deux fractions qu’il faut additionner (ou
soustraire) : 1°) rendre irréductible les deux fractions.
2°) Calculer le Plus Petit
Dénominateur Commun : (des dénominateur des
fractions rendues irréductibles 3 / 7
et 4 / 11 ; les dénominateur)
Cela revient à calculer le Plus Petit Commun Multiple (appelé PPCM
;objectif n°32
) des deux dénominateurs (7 et 11 ).
Le PPCM de 7 et 11 est 77 3°) Transformer chaque fraction
( 3 / 7 et 4 / 11 ) en fraction équivalente dont le nouveau
dénominateur sera égal au PPDC calculer précédemment ( 77 ). (Voir procédure pour transformer une fraction
en fraction équivalente ,objectif N° ...) Rappel: pour transformer une fraction en fraction équivalente il
faut multiplier le numérateur et le dénominateur par un même nombre ,non nul. a) Transformation de la
première fraction en fraction équivalente de dénominateur égal au PPDC (ici 77 ) : b)
on calcule
77 : 7 ;on
trouve le nombre « k » =11 (il faut donc multiplier le numérateur par
11). Ce qui donne b) Transformation de la deuxième fraction en fraction équivalente de
dénominateur égal au PPDC (ici 77) la deuxième fraction on calcule :
77 : 11 = 7 (on doit donc multiplier le numérateur par
7) ce qui donne: (voir page suivante le rappel
sur le détail de la transformation) 4° )
Rendre compte sous forme d’une égalité: Le couple de fractions de départ étant égal au couple de fractions
obtenus après transformation.
CONCLUSION : Nous avons ainsi obtenu un nouveau couple de
fractions ( IL faut toujours vérifier: Pour savoir si : a) La fraction b) La fraction Il faut faire le
produit en croix Exemple: pour vérifier si 33 / 77
est équivalent à la fraction 6 / 14 ,il
suffit de faire le produit en croix
pour vérifier si l’égalité 6 x
77 et 33 x 14 est vraie. 6 fois 77 = 462 33 fois 14 = 462 Faites en autant avec les fractions 12 / 33 et 28 / 77
Commentaire : lorsque l’on veut additionner ou soustraire deux fractions de dénominateur
différent il faut impérativement passer par ces calculs; lorsque les deux
fractions sont réduit au même dénominateur on
applique la règle concernant l’addition ou la soustraction de deux
fraction de même dénominateur. |
|
||||
|
|
Réduire (mettre) au même dénominateur les termes suivants: |
|
||||
|
|
|
|
|
|||
|
N°1 : |
|
|||||
|
|
Calcul du
PPDC de
|
|||||
|
N°2 |
|
|||||
|
|
Le PPDC de
|
|||||
|
N°3 |
|
|||||
|
|
Le PPDC de
|
|||||
|
|
|
|||||
|
|
SOIT
l'égalité suivante, il faut la transformer en vue de résoudre: |
|
|
|||
|
|
On transforme l'égalité
|
Pour devenir une égalité équivalente:
|
|
|||
|
|
|
|
|
|||
|
|
Explications: |
|
|
|||
|
|
Soit l'expression |
|
|
|||
|
|
|
|
|
|||
|
|
1°) On transforme le deuxième terme |
|
|
|||
|
|
2°) On transforme le troisième terme |
|
|
|||
|
|
3) On remplace dans la première expression, les nouveaux termes.
|
Pour devenir:
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||