Pré requis:
|
Savoir
: réduire au même dénominateur deux fractions |
|
|
Savoir
: transformer N en fraction équivalente à une autre fraction dont on
impose un dénominateur. |
|
ENVIRONNEMENT du dossier :
|
Objectif précédent |
Tableau
|
DOSSIER : FRACTION EQUIVALENTE à
une autre fraction dont le dénominateur
est donné.
- A)
Définition
- B ) vérifier si deux fractions sont équivalentes.
- C) construire une fraction équivalente.
|
|
COURS |
Devoir Contrôle |
Interdisciplinarité
|
|
|||
|
|
|
|
|
|
Devoir :
niveau 5 |
||
A) Définition de l ‘ objectif : Savoir construire une fraction égale à une fraction
donnée.
Rappels
A ) FRACTION EQUIVALENTE *(à
une autre fraction): *Cette notion est trés
importante; elle est la clef du travail sur les proportionnalités.
Equivalente
: veut dire « de même valeur »; donc on dira que : deux fractions dites
« équivalentes » sont des fractions qui représentent la même
valeur.(racine latine :« équi » qui signifie « égal »)
-Remarque. Des
fractions (ou écriture fractionnaire ) peuvent
représenter un même nombre:
Exemples
:
Le résultat du calcul des divisions suivantes
(quotient ) est identique ( de même valeur) 48 / 12 = 4 ;
20 / 5 = 4 ; 4,8 /
1,2 = 4
; 4 / 1 = 4
De ce constat , on peut
donc écrire que 
= 
= 
= 
= 4
B ) Deux fractions
séparées par le signe « égal » sont dites
« fractions équivalentes »
Modèle mathématique:
« a » ; « b » ;
« c » ; « d »
sont des nombres entiers .
=
(il faut
que « b » et
« d » soient différents de 0)
Question : pour rechercher l’équivalence de deux fraction ( Q : SONT -
ELLES « EQUIVALENTES » ? ? ? ? ?)
On répondra « OUI » , si
le résultat de la multiplication (que
l’on appelle :produit ») du nombre « a » par le nombre « d » est
égal au produit du nombre
« b » par le nombre « c ».
Ainsi et sont équivalentes
si ... « le
produit......."a d " est
égal au produit "c b" »
Le calcul de
... « le produit......."a d " est égal au produit
"c b" » est appelé « produit
en croix »
Exemple numérique (on reprend les fractions ci dessus, on sait quelles
sont égales ) :
Exemple : Enoncé : Dire si Les fractions et sont équivalentes ??????
Ou : cet énoncé se
résume à l’écriture suivante :
= ?
Deux possibilités pour répondre : 1°) on
fait les divisions pour chaque fractions et l’on compare les quotients ,
2°) ou
l’ on calcule le produit en croix
.
Première
possibilité :
On effectue les opérations : 48 : 12 = 4 ;
20 : 5 = 4
Conclusion
n° 1 : La réponse est « oui » : les deux fractions sont
équivalentes.
Des
fractions équivalentes représentent un
même nombre ,un même rationnel ; (que l'on appellera coefficient de proportionnalité)
Deuxième possibilité :
Soit les fractions et
On calcule 48 fois 5 ; et on calcule 12 fois 20 .
48 fois 5 = 240
; 12 fois 20 = 240
Constat :
les deux multiplications ont le même produit « 240 » ; 48 fois 5 = 12
fois 20 donc 240 =
240
Conclusion : les
fractions et sont
équivalentes on peut écrire
l’égalité suivante : =
C ) Procédure
pour construction d’une fraction équivalente (à une fraction donnée)
Pour construire une
fraction équivalente à une fraction donnée il suffit de multiplier le
numérateur et le dénominateur de la fraction par un nombre entier.
Modèle mathématique:
on
multiplie a et b par k 
=
=
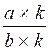attention :
k Î N ( lire : le
nombre « k » est un nombre entier )
Exercice
type :
Enoncé :
construire (ou donner ) une fraction équivalente à la
fraction 
Résolution :
si je multiplie le num. « 7 »
(Numérateur) et le déno. « 21 »
(Dénominateur) par 2 j’obtiens la fraction :
rédaction : = 
=
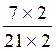si je multiplie le num.
« 7 » (Numérateur) et le déno.
« 21 » (Dénominateur) par 3
j’obtiens 
la fraction : 
=
=,
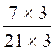il y a une
infinité de solutions
( On
aurait pu proposer de diviser par « 7 » et obtenir la fraction 
)
Conclusion: on peut proposer plusieurs
solutions de fractions équivalentes à
la fraction de départ et écrire que = (lire « est équivalente
à » )
ou
que =
ou que = 
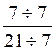* = *7 /7 =1 et
21/7=3
Remarques:
1. - On
peut obtenir une infinité de fractions équivalentes à une fraction donnée en
multipliant le numérateur et le dénominateur par un même nombre
..
2.
- On peut aussi obtenir une fraction équivalente en
divisant le numérateur et le dénominateur par un nombre entier non nul ,mais dans ce cas on limitera le nombre de
fractions équivalentes ,puisque nous
arriverons à la fraction irréductible.
IMPORTANT: Deux
fractions sont équivalentes si .......on
peut le vérifier ?
Vérification: Il y a deux
solutions différentes :
Première
solution
: On prend
une calculatrice ,on effectue les divisions relatives
à chaque fraction et l’on compare les deux résultats.(Il restera toujours un
doute notamment lorsque l’on divise des fractions irréductibles très proche ;
puisqu’elles n’ont pas de valeur décimale exacte).
(
Cette méthode peut être très utile pour classer des fractions ,les unes
par rapport aux autres)
exemple type I : elles ne sont pas équivalentes
Question: La fraction 11 / 15 est-elle équivalente à la fraction 13 / 17
? (Si non ,on
pourrait alors demander de les classer par ordre ...croissant )
Réponse:
11 : 15 = 0.7333333
13 : 17 = 0.764705
conclusion: les fractions 11 /15
et 13 / 17 ne sont pas
équivalentes.
(Dans ce cas
,pour la question suivante , on peut écrire que 13 / 17
> 11 /15 )
exemple type II : elles sont équivalentes
Question :La fraction 22 /30
est-elle équivalente à la fraction
583/795 ?
Réponse:
22 : 30 = 0.733333333
583 :795 = 0.73333333
Conclusion :on ne peut conclure ,en étant certain : « elles pourraient être
équivalentes ».
Si on ne peut conclure ,dans ce cas voir la
solution suivante
Deuxième
solution: (la plus sure) ;
Procédure permettant de vérifier si deux fractions
sont équivalentes:
Pour
s’assurer (ou vérifier) que
deux fractions sont
équivalentes, il suffit de transformer l’égalité des deux fractions.
1°) On
transforme ce Modéle
mathématique:
=
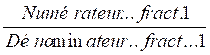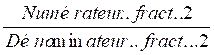
en une égalité de deux produits:
en ce modèle mathématique:
Numérateur..fract.1 x
Dénominateur .fract. 2 =
Numérateur fract.2 x Dénominateur fract 1
2°) On effectue les multiplications
3°) et on compare les résultats
4°) On conclut:
a) si les produits sont égaux ;les fractions sont dites
équivalentes.
b)
si les produits ne sont pas égaux ;les
fractions données ne sont pas égales
Exemple:
On reprend l’exercice
précédent:
Enoncé : La fraction 22 /30
est-elle équivalente à la fraction
583/795 ?
On
applique la procédure:
On énonce:
est égale à 
si 22 x
795 est égal à 583 x 30
On effectue les calculs:
22 x
795 =
17 490
583 x
30 = 17 490
On compare les résultats : 22 x 795 est égal
à 583 x 30 ( 17490=17490)
On tire une Conclusion: les fractions 
et sont équivalentes; on
peut donc écrire =
En résumé:
Deux fractions (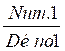
et 
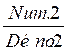) sont
équivalentes (c’est à dire) : 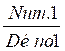= 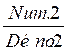si Num.1 x
Déno.2 = Num.2 x Déno.1
Traduction
en langage littérale:
Deux fractions sont équivalentes
si le produit du numérateur de la première fraction par le dénominateur de la
seconde fraction est égal au produit du numérateur de la deuxième fraction par
le dénominateur de la première fraction.
Remarques importantes:
On
appelle cette méthode :@ « le produit en
croix. »
Lorsque nous aborderons la leçon sur les
proportionnalités on dira:
que le
produit des extrêmes est égal au produit des moyens , (les extrêmes
étant Num.1 et Déno.2, les moyens
étant Déno.1 et Num.2)
= 
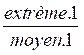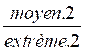si extrème.1 x
extreme.2 = moyen.1 x moyen.2
Applications :algèbre « résoudre »
avant
de résoudre il faut transformer l ‘égalité donnée ;en
appliquant le produit en croix
|
|
|
|
|
|
|
|
|
|
5x
=12 |
|
7 |
|
7x=3 |
|
7 |
|
3La règle de trois est un "procédé" de
calcul permettant d ' étudier la variation
de deux grandeurs proportionnelles.
La règle de trois s ’ applique
à la forme mathématique :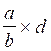 
= ? (= c )
|
Voir: La multiplication
d'un nombre ( ou grandeur) par une fraction |
|
Ce qui donne le modèle :
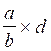(qui ne se calcule pas ) devient le produit
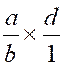qui lui peut se calculer
pour devenir le calcul :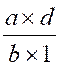 
devient après calcul
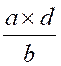
si
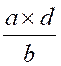= c
cette
écriture peut et doit se transformer
sous la forme =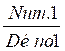
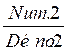
pour donner = ; * l ‘ égalité est vraie si : ad = bc
Nous obtenons le produit « en croix » suivant :
a 
d = c b
Conclusion : la "règle de trois" est une transformation
du "produit en croix" ,pour régler la recherche d'une quatrième grandeur (appelée "quatrième
proportionnelle" ).
CALCULS PARTICULIERS
forme : « @ une fraction est égale à un nombre »
= c ; on
recherche ou « a » ou « b »
Alors faire la transformation :
= 
est effectuer le produit en croix .tel
que : a 1 = c b ;soit :
a = cb
ou = devient 
= b ;pour
obtenir b = 
EXERCICES : Transformer l’égalité ,
par le produit en croix , (ne pas faire le calcul)
a )
= 5
; b
) 
= 7 ;
réponses :
a) x = 13 5 ;
b )
13 = 7 x
TRAVAUX AUTO FORMATIFS.
1° ) Dans quel domaine des mathématiques utilise-t-on les
fractions équivalentes ?
2 ° ) Par quel signe sont séparées deux fractions
équivalentes?
3° ) Que signifie le mot :équivalentes?
4 ° ) Donnez le modèle
mathématique représentant deux fractions équivalentes.
5 ° ) Donnez la procédure
permettant d’obtenir une fraction équivalente à une fraction donnée,donnez le
modèle mathématique.
6° ) Comment peut-on
procéder pour ordonner ( classer dans un
ordre croissant ou décroissant ) des
fractions ?
7° ) Comment procède -t -
on pour vérifier si deux fractions sont équivalentes (donnez la procédure la
plus sûre ) ?
8 ° ) Enoncer la procédure
permettant d’effectuer « le produit en croix ».
I )Dire si les fractions suivantes sont équivalentes
(si non les classer par ordre croissant):
a ) 
; 
; 
; 
;
; utiliser le
tableau ci dessous ;
b )idem que ci dessus : 
;
;
;
;
c ) idem que ci dessus : ;
; 
II ) Construire
.....5......fractions équivalentes à la fraction donnée : 
III) On nous donne deux fractions ;
et 
;sont-elles
équivalentes?
En complément :voir cas
avec nombres relatifs
I ° ) Construire 3 fractions équivalentes à la
fraction donnée.(indiquer le coefficient multiplicateur utilisé pour chaque
étape)
*un « coefficient » est un nombre ,généralement
, entier .
a) 
=
b) 
=
c) 
=
d) 
=
II ° ) CALCUL ALGEBRIQUE :
Transformer , par le
produit en croix , les fractions équivalentes :
|
|
|
|
|
|
|
|
|
et encore :
a) = 5
b) = 7 ;
Construire 4
fractions équivalentes à la fraction à la donnée
a) 
=
b) 
=
c) 
=
d) 
=
e)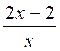 
=
f)
=
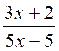CORRIGE EVALUATION
I ) a) ligne 2 : calcul avec la calculatrice
ligne 3 : classement par ordre croissant.
|
|
|
|
|
|
|
0,28333 |
0,250 |
0,8337 |
0,583 |
0,600 |
|
2 |
1 |
5 |
3 |
4 |
|
|
|
|
|
|
conclusion : 
<< <<
|
Applications : en sciences , LES PROPORTIONNALITES |
|