|
CAP et niveau V |
DOSSIER : LES
GRANDEURS PROPORTIONNELLES / Objectif cours 30 |
|
|
|
|
|
|
|
|
|
|
Fraction
équivalente |
|
|
|
|
|
Produit en croix |
|
|
|
|
|
Objectif
précédent : |
Objectif
suivant : |
Liste des cours sur les proportions et
les inversement proportionnels |
DOSSIER:
LES
GRANDEURS PROPORTIONNELLES (leçon
N°2/…)
LA
PROPORTION et LA QUATRIEME PROPORTIONNELLE
|
TEST |
COURS |
Devoir Contrôle |
Devoir évaluation |
Interdisciplinarité |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rapport :
I
) PROPORTION :
On appelle « proportion »
l’égalité se deux rapports.
Relations qui existent entre les
mots :
|
« fraction » |
« rapport » |
« rapports égaux » |
« fractions équivalentes » |
« proportion » |
|
|
fraction |
= |
rapport |
|
égalité de deux fractions |
= |
fractions
équivalentes |
|
fractions
équivalentes |
= |
rapports
égaux |
|
rapports
égaux |
= |
égalité
de deux fractions |
|
rapports
égaux |
= |
proportion |
|
égalité
de deux fractions |
= |
proportion |
Donc : nous pouvons dire qu
‘ une proportion est l’égalité de deux fractions.
Modèle
mathématique :
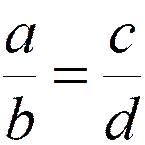
RAPPEL
: les fractions équivalentes ;
vérification :
En résumé:
Deux fractions (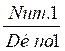
et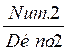 
) sont
équivalentes (c’est à dire) :
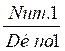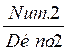= si Num.1 x
Déno.2 = Num.2 x Déno.1
Applications algébriques :
soit l’égalité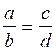 
ont
peut donc écrire a
d = c b
Commentaire : on
voit que d’une proportion ,on peut obtenir par
transformation , l’égalité de deux produits
Cette égalité de produits se peut ,à nouveau , se transformer
dans le but de trouver une autre égalité
permettant de trouver a = .....; b =...... ; c =....... ; ou d =.......
;
transformations :
; 
; 
; 
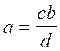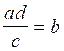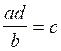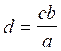
Applications numériques :
Trouver la valeur de « x » , (pour que
l’égalité reste vraie)
; 
; 
; 
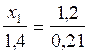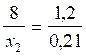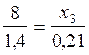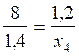
Le petit périmètre d’un carré = 36 mm ; le
rapport entre le petit et le plus grand est de ¼ ; quel est le périmètre
du grand carré ?
réponse :
Þ x = 4 fois 36 ; soit x
= 144 mm
AUTRE
VOCABULAIRE utilisé dans le
calcul du
"produit en croix":
L’écriture
mathématique:
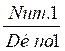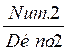= si Num.1 x
Déno.2 = Num.2 x Déno.1
sera remplacé par :
pour la première fraction : (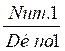) par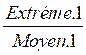 
le numérateur de la première fraction s’appellera : Extrême 1
le dénominateur de la première fraction s’appellera :
Moyen 1
pour la deuxième fraction : 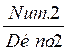par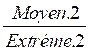 
le numérateur de la deuxième fraction s’appellera : Moyen 2
le dénominateur de la deuxième fraction s’appellera :
Extrême 2
Ce qui donne :
=
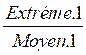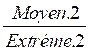
et l 'on
énoncera
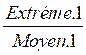est
égale à 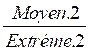si
Extréme.1 "fois" Extréme.2
= Moyen .2 "fois" Moyen.1 ;
EN RESUME
Nous
pouvons énoncer :
I ) Dans une proportion, le produit des extrêmes est
égal aux produits des moyens.
Traduction mathématique : si
= 
alors ad = cb
II) Dans
une proportion, on peut permuter les « extrêmes »« ( l’égalité reste vraie)
Traduction mathématique : si = alors 
= 
III) Dans
une proportion, on peut permuter les « moyens » ,(l’égalité
reste vraie)
Traduction mathématique : si = alors 
= 
II ) QUATRIEME PROPORTIONNELLE :
Remarque :
Lorsque l’on connaît 3 valeurs sur 4 ,dans une
proportion, on peut trouver la « quatrième » valeur . On dira «
rechercher la quatrième proportionnelle. »
Procédure :
Pour calculer
la quatrième proportionnelle il faut
faire le produit en croix ,faire le calcul avec les deux
nombres ;diviser les deux membres de l’égalité par le nombre
multiplicateur de « x »
Exemple : trouver la valeur de
« x » dans :
=
« x »
est la quatrième proportionnelle .
Résolution : 7,5 x
= 15 fois 2,3 :
7.5 x divisé par 7.5 =
15 multiplié par 2.3 divisé par 7.5
x = 4.6
TRAVAUX AUTO – FORMATIFS :
I ) Dans une proportion comment
appelle-t-on ?:
1) le
numérateur de la première fraction
2) le
dénominateur de la première fraction
3 )le numérateur de la deuxième fraction
4 )le dénominateur de la deuxième
fraction
II ) Qu’appelle-t-on
« proportion » ?
1 ) A quoi est égal deux rapports égaux ?
2 ) Quel est le modèle mathématique pouvant
représenter des rapports égaux ?
III ) On
donne deux rapports égaux :
1 )
Comment nomme-t-on le numérateur de la première et le dénominateur de la
seconde fraction ?
2 )
Comment nomme-t-on le dénominateur de la
première et le dénominateur de la seconde fraction ?
IV )
Enoncer les règles faisant intervenir les extrêmes et les moyens.
(donner un modèle mathématique et ensuite
accompagner ces modèles d’application numérique.)
V ) Dans quel cas dit-on que l’on recherche la quatrième
proportionnelle ?
De l’égalité 3,4 x 7,8 = 2,4
x 11,05 ; déduire toutes les proportions possibles.
Idem que ci dessus :
6,03 x 0,25
= 4 ,5 x 0,335
Calculer
« x » dans chacun des cas
suivants :
|
|
|
|
|
a)
x
ATTENTION !!!! Le signe « multiplier »
n’est pas tracé en algèbre on mettra toujours le nombre en tête |
On remplace l’écriture : x |
|
|
b) 6,5 x = 46,15 |
|
|
|
c) 11,2 = 3,2 x |
|
|
|
d) 7,56 = x |
|
|
Calculer x dans chacun des cas suivants :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Des connaissances
e n sciences sont nécessaires pour comprendre le
travail demandé ; (à vous de vous
informer :
1°)
Calculer la mesure de la d.d.p. aux bornes d’un
résistor dans les cas suivants :
|
calibre |
Echelle |
lecture |
|
|
3 V |
[ 0 ; 30 [ |
22
divisions |
|
|
10 V |
[ 0 ; 100 ] |
57
divisions |
|
|
300
V |
[ 0 ; 30 [ |
25
divisions |
|
2°)
Quelle est l’intensité du courant traversant le circuit ?
|
Calibre |
Echelle |
lecture |
|
1 A |
( 0 ; 100 ) |
83
divisions |
|
0,1
A |
( 0 ; 100) |
57 divisions |
3°) Une voiture consomme 18,4 l d’essence pour
effectuer le trajet Paris - Caen ( 230 km) .Quelle sera sa consommation pour effectuer le
trajet Paris - Cherbourg
long de 340 km ?
Que devons nous admettre pour résoudre le problème ?
4°) La
masse et le volume d’un corps sont deux grandeurs directement proportionnelles
.Le coefficient de proportionnalité s’appelle la « masse volumique »
du corps.
a) Calculer
le volume d’un corps de masse 52 kg dont
la masse volumique est de 23 kg /dm3
b) Calculer
la masse d’un corps de volume 3,5 dm3 dont la masse volumique est de 7,8 kg /
dm3.