|
|
|
|
CORRECTION GRANDEURS
PROPORTIONNELLES …LA PROPORTION
|
|
|
|
|
Interdisciplinarité
|
|
Des connaissances en
sciences sont nécessaires pour comprendre le travail demandé ; (à vous de vous informer :
1°) Calculer la mesure de
la d.d.p. aux bornes d’un résistor dans les cas suivants :
|
calibre |
Echelle |
lecture |
corrigé |
|
3 V |
[ 0 ; 30 [ |
22 divisions |
x =22,1 V |
|
10 V |
[ 0 ; 100 ] |
57 divisions |
x =5,7 V |
|
300 V |
[ 0 ; 30 [ |
25 divisions |
x =250 V |
2°) Quelle est l’intensité
du courant traversant le circuit ?
|
Calibre |
Echelle |
lecture |
|
1 A |
( 0 ; 100 ) |
83 divisions =
x = 0,83 A |
|
0,1 A |
( 0 ;
100) |
57 divisions ==
x = 0,057 A ou 57mA |
3°) Une voiture consomme 18,4 l d’essence pour
effectuer le trajet Paris - Caen ( 230
km) .Quelle sera sa consommation pour effectuer le trajet Paris
- Cherbourg long de 340 km ?
Que devons nous admettre
pour résoudre le problème ?
|
On pose:
|
x = 27,2 l |
|
Conclusion: Nous considérons que la consommation
est constante |
La consommation pour 340 km parcourus
sera de 27,2 litres |
4°) La masse et le volume
d’un corps sont deux grandeurs directement proportionnelles .Le coefficient de
proportionnalité s’appelle la « masse volumique » du corps.
a)
Calculer le volume d’un
corps de masse 52 kg dont la masse
volumique est de 23 kg /dm3
|
On pose :
|
Calcul: 52 fois 1 :23 |
|
Volume = 2,2608696 dm3 |
|
b)
Calculer la masse d’un
corps de volume 3,5 dm3 dont la masse volumique est de 7,8 kg / dm3.
Réponse : Masse du corps = 27,3 kg
I ) Dans une proportion comment
appelle-t-on ?:
1) le numérateur de la
première fraction : Dans une proportion le numérateur de la première
fraction s’appellera : Extrême 1
2) le dénominateur de la première fraction: Dans une proportion le dénominateur de la première fraction s’appellera :
Moyen 1
3 )le numérateur de la
deuxième fraction : Dans une proportion le numérateur de la deuxième
fraction s’appellera : Moyen 2
4 )le dénominateur de la deuxième fraction : Dans une proportion le dénominateur de la deuxième fraction s’appellera :
Extrême 2
II )
Qu’appelle-t-on « proportion » ? On appelle « proportion » l’égalité
se deux rapports.
1 ) Que
forment deux rapports égaux ? Deux rapports égaux
une proportion
2 ) Quel est le modèle mathématique pouvant
représenter des rapports égaux ?
Modèle mathématique : 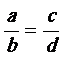
III )On donne deux rapports égaux :
1 ) Comment nomme-t-on le numérateur de la première
et le dénominateur de la seconde fraction ? Dans
deux rapports égaux le numérateur de la première et le dénominateur de la
seconde fraction s'appellent les
extrêmes
2 ) Comment nomme-t-on le dénominateur de la première et le dénominateur de la seconde
fraction ?
Dans deux rapports égaux le
dénominateur de la première et le
dénominateur de la seconde fraction s'appellent les moyens
IV ) Enoncer les règles faisant intervenir les
extrêmes et les moyens.
(donner
un modèle mathématique et ensuite accompagner ces modèles d’application
numérique.)
Dans une proportion, le produit des extrêmes
est égal aux produits des moyens.
Traduction mathématique :
si ![]() =
= ![]() alors ad = cb
alors ad = cb
V ) Dans quel cas dit-on que l’on recherche la
quatrième proportionnelle ?
Lorsque l’on connaît 3 valeurs sur 4
,dans une proportion, on peut trouver la « quatrième » valeur . On
dira « rechercher la quatrième proportionnelle. »
1 ) De
l’égalité 3,4 x 7,8 = 2,4 x 11,05 ; déduire toutes les
proportions possibles.
On sait que ![]() est égale
à
est égale
à ![]() si
si
Extréme.1
"fois" Extréme.2 =
Moyen .2 "fois" Moyen.1 ;
a) On remplace :
3,4 "fois" 7,8
= 2,4 "fois" 11,05
b) on remplace dans :
![]() est égale
à
est égale
à ![]()
On sait que : Dans une proportion, on peut permuter les
« extrêmes »« ( l’égalité reste vraie)
traduction mathématique
si ![]() =
= ![]() alors
alors ![]() =
= ![]()
si ![]() =
=![]() alors si
alors si ![]() =
=![]()
Dans une proportion, on peut permuter les « moyens »
,(l’égalité reste vraie)
traduction mathématique
si ![]() =
= ![]() alors
alors ![]() =
= ![]()
donc : si ![]() =
=![]() alors si
alors si ![]() =
=![]() ou
ou ![]() =
=![]()
Solutions
|
|
|
|
|
|
|
|
|
|
|
|
Idem
que ci dessus :
|
6,03 x 0,25
= 4 ,5 x 0,335 |
|
|
|
|
|
|
Calculer
dans chacun des cas suivants :
|
|
|
|
|
x |
x=8,88 fois0,37 |
3,2856 |
|
6,5 x = 46,15 |
x =46,15:6,5 |
7,1 |
|
11,2 = 3,2 x |
x =11,2 : 3,2 |
3,5 |
|
7,56 = x |
7,56 : 0,9 = x |
8,4 |
Calculer x dans chacun
des cas suivants :
|
|
|
|
|
|
x = 2,3 fois 15 : 7,5 = |
4,6 |
|
|
x= 87,12:9,9 |
8,8 |
|
|
x= 1,76:6 |
0,88/3 = 88/300 |