|
DOSSIER : LES GRANDEURS
PROPORTIONNELLES / Objectif cours 29 |
|
Les grandeurs proportionnelles et inversement
proportionnelles (notions) |
|
|
Produit en
croix (pour vérifier si deux rapports
sont égaux) |
|
Objectif précédent : 1°)La proportionnalité et tableau à quatre nombres . |
Objectif suivant : |
DOSSIER : LES GRANDEURS PROPORTIONNELLES …leçon N°1
1. RAPPORT
2.
RAPPORTS EGAUX
3. SUITES DE
RAPPORTS EGAUX et coefficient de
proportionnalité
|
TEST |
COURS |
3°) voir
« Thales » et les quotients ou rapports égaux…. |
|
Rapport :
On appelle « rapport » est le quotient de la division d’un nombre par un
autre nombre.
Le modèle
mathématique d’un « rapport » est « une fraction ».
Exemple :
le rapport de 1 à 5 est représenté par
la fraction :![]()
On appelle
« rapport géométrique » de « a » à « b » , ou
simplement rapport de « a » à « b » , l’expression a :
b ; ou ![]() ( division
« a » par « b ») .
( division
« a » par « b ») .
« Rapport » ; « fraction »
et « quotient » sont des mots
équivalents qui mène à la « division ».
Rapports
égaux :
On appelle « rapports égaux » est l’égalité des quotients des divisions de deux nombres
( les divisions ont le même quotient et dont le reste des divisions est nul .
(on dit aussi :quotient
exact )
Le modèle
mathématique de deux rapports égaux est l’égalité de
deux fractions.
Traduction en
langage mathématique : 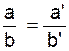
*
Lecture : a’
lire « a prime » ; b’ lire « b prime »
Remarque : l’égalité de deux
rapports peut écrire aussi 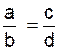
Exemple de l’égalité de deux rapports : 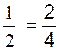 ( à
vérifier)
( à
vérifier)
Suite de rapports égaux et le
coefficient de proportionnalité : (Info
sur le mot « suite » )
Lorsque nous avons plus de deux
rapports égaux nous pouvons dire que nous avons une « suite de rapports égaux » , le quotient de chaque rapport étant identique , c’est un
nombre dit constant appelé « k ».
Ce nombre est
appelé : « coefficient de proportionnalité »
Traduction en
langage mathématique : 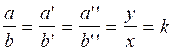
Pour
l’écriture « a’’ » : lire « a » seconde ; et pour l’écriture « b’’ » :
lire
« b » seconde.
Traduction en
langage littéral :
« a sur b » est égal à « a prime » sur « b prime » est égal à « a seconde » sur « b seconde . »
remarque importante ,et à retenir :
par
convention ; le coefficient de proportionnalité noté
« k » sera toujours égal au rapport « y » sur « x » ; cette écriture est a mettre en relation
avec le « y » et le
« x » du repère cartésien.
k = ![]() ; donc
inversement
; donc
inversement 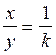 (par conséquence le rapport
x / y sera égal à la fraction
1 / k )
(par conséquence le rapport
x / y sera égal à la fraction
1 / k )
Exemple
d’application : (Toujours se rappeler que ![]() = k
)
= k
)
on nous donne
4 rapports ( ![]() ;
; ![]() ;
; ![]() ;
; ![]() ) sont-il égaux ?
) sont-il égaux ?
Recherche :
A ) pour chaque rapport nous pouvons calculer
le «coefficient : k » :
premier
rapport : 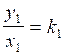 ;appliquons :
;appliquons : ![]() =1,5
=1,5
deuxième
rapport : 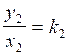 ;
appliquons :
;
appliquons : ![]() = 1,5
= 1,5
troisième
rapport : 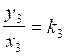 ; appliquons :
; appliquons : ![]() = 1,5
= 1,5
quatrième
rapport : 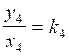 ;
appliquons :
;
appliquons : ![]() = 1,5
= 1,5
B ) analyse :nous constatons que k1 ; k2 ; k3 ;
k4 sont égaux.
C) Conclusion : le coefficient K est identique
pour chaque rapport ,nous pouvons écrire l’égalité
suivante :
![]() =
= ![]() =
= ![]() =
= ![]()
Vérification : Pour vérifier si la suite de rapports est
une suite de rapports égaux il faut faire le produit en « croix » , chaque
égalité : ![]() =
= ![]() ( 3 fois4 égal 2
fois6)
( 3 fois4 égal 2
fois6)
;
![]() =
= ![]() (6 fois 6 égal 4 fois9 ) et
(6 fois 6 égal 4 fois9 ) et ![]() =
= ![]() (9 fois 9 égal 6 fois
13,5 ) .
(9 fois 9 égal 6 fois
13,5 ) .
Commentaire : quelque soit la méthode de
vérification elle est longue et parfois peut fiable ;c’est
à partir d’un constat que nous allons appliquer une méthode plus rapide.
PROCEDURE :
Construire une
autre fraction : avec les fractions équivalentes données.
Cette autre
fraction aura pour numérateur : le numérateur égal à la somme des numérateurs et pour
dénominateur égal à la somme des
dénominateurs .
(ATTENTION ! ! ! cette pratique n’est pas la somme de deux fractions ,c’est simplement la
construction d’une fraction équivalente à des fractions déjà équivalentes ,
se souvenir que dans
l’addition de deux fractions :
1°)
elle n’est possible que si les dénominateurs sont identiques.
2°)quand les dénominateurs sont identiques ,on fait seulement
l’addition des numérateurs)
Application :
les deux fractions suivantes sont équivalentes (il faut toujours vérifier l’équivalence)
![]() et
et ![]() ; pour obtenir une
autre fraction équivalente ,je fais les
deux additions 3+6 =9 (somme des numérateurs) et 2+4
= 6 (somme des dénominateurs); j ’ écris la nouvelle fraction
« équivalente » donc j’obtient la fraction
; pour obtenir une
autre fraction équivalente ,je fais les
deux additions 3+6 =9 (somme des numérateurs) et 2+4
= 6 (somme des dénominateurs); j ’ écris la nouvelle fraction
« équivalente » donc j’obtient la fraction ![]() .
.
Vérification :
si je fais la division de 9 par 6 je trouve 1,5 ; (valeur égale à "k")
Par extension :
Je peut opérer de la même
façon avec toutes
les fractions de la « suite de
fractions »
donnée :
soit la suite
de fractions , sont-elle
équivalentes ?
![]() =
= ![]() =
= ![]() =
= ![]() ;
;
(si les fractions données sont équivalentes, je
peut construire une autre fraction équivalente qui aura pour numérateur la somme
des numérateurs et pour dénominateur la somme des dénominateurs, ensuite je vérifierai pour cela deux solutions :
- la
division du numérateur par le
dénominateur pour trouver le
« k ».
ce qui me donne
l’opération 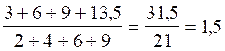
j’obtient ,une fois encore, la valeur
« k » de 1,5
- Ou
alors je prendrai une fraction donnée au hasard et je ferai le produit en croix
pour vérifier l’égalité des produits.)
On remarque
qu’avec des fractions dites « égales » ,si on additionne les
numérateurs entres eux et si l’on additionne les dénominateurs entres eux ,et
si l’on met ces résultats sous forme de fraction ,on obtient une autre fraction
égale aux précédentes.
CONCLUSION :
Avec une suite de rapports égaux,on forme un autre rapport(ou fraction) égal à chacun
d’eux ( de chaque rapport) qui aura
pour numérateur la somme des numérateurs et pour dénominateur la somme
des dénominateurs .
traduction en langage mathématique :
si ![]() =
= ![]() =
= ![]() =
= ![]() ; alors on
a
; alors on
a 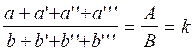
Commentaire : on peut donc
dire qu’une suite de rapports (ou de grandeurs ) sont
proportionnels si la somme des numérateurs sur la somme des dénominateurs (de tous les
numérateurs et dénominateurs de ces rapports) forme une proportion avec
un des rapports de cette suite.
Procédure de
vérification :
faire le produit en croix, (ou faire la division pour les deux rapports
et comparer le quotient ).
REPRESENTATION
GRAPHIQUE D’UNE SUITE DE RAPPORTS PROPORTIONNELS :
Voir l’
objectif sur les repères ( Sauf cas particulier et dans ce cas signalé
nous travaillons dans un repère cartésien Orthonormé)
La
représentation d’une suite de rapports non
proportionnels est un ensemble de points non alignés
,dans un repère.;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() La représentation d’une suite de rapports proportionnels est un ensemble
de points alignés, qui ont pour particularités de tous se trouver
sur une droite
La représentation d’une suite de rapports proportionnels est un ensemble
de points alignés, qui ont pour particularités de tous se trouver
sur une droite
Représenter les deux suites dans le repère ci -
dessus :
Les
deux suites des « x »[
9 ;11 ;19 ;25 ;31 ;]
et des « y » [27 ; 33 ;57 ;75 ;93 ;]
sont elles proportionnelles ?
Réponse : oui si tous les couples de nombres se
trouve sur une droite.
TRAVAUX AUTO
FORMATIFS.
1 ) Qu’est ce qu ’ « un rapport » ?
2 ) Donner un modèle mathématique d ’ un rapport.
3 ) Qu’appelle-t-on
« rapports égaux » ?
4 ) Donner un modèle mathématique de « rapports égaux »
5 ) Donner une suite de rapports égaux.
6 ) Que peut-on former à partir d’une suite de rapports égaux ?
7 ) Traduire en langage mathématique ce que vous avez
énoncé précédemment
8 ) Combien a - t - on de moyens de vérifier si deux
rapports sont proportionnels ?
(donner la
procédure d’exécution pour chaque ,vous pouvez vous
aider de nombres)
9 ) Que peut - on construire avec une suite de
rapports égaux ?(donner le modèle mathématique)
10 ) Pour vérifier si une suite de rapports sont égaux
,que fait - on ?
11 ) Que signifie cette écriture mathématique ?
si ![]() =
= ![]() =
= ![]() =
= ![]() ; alors on
a
; alors on
a 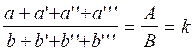
12 ) Comment peut-on vérifier si une suite de nombres
(ou de grandeurs) est proportionnelle ?
(Donner un
exemple).
1°) Construire
une suite de deux rapports non égaux ;
justifiez
a) avec des nombres
b) avec des lettres
2°) Construire
une suite de deux rapports égaux ;
justifiez.
a) avec des nombres
b) avec des lettres
3°) Les deux
suites [
9 ;11 ;19 ;25 ;31 ;]
et [27 ;
33 ;57 ;75 ;93 ;] sont -elles des suites de nombres
proportionnelles ?
4°) Même question :
pour : [ 7 ;13 ;17 ;28] et [
77 ;130 ;180 ;309 ]
5°) Même
question pour [5,2 ;7,9 ;13,4 ;18,9] et [
21,84 ;33,18 ;56,28 ;79,38 ]
A) Si l’on paye dans un
restaurant 2400f pour
un mois de pension ,que paiera-t-on pour :
5jours ;
12jours ; 21 jours
B) Un fumeur fume un paquet de tabac de 17,50 f ,tous les cinq jours ;combien
dépense-t-il par semaine ?
.voir
livre M ROYER et P.COURT librairie Armand Colin Classe CEP