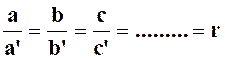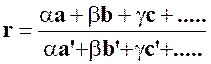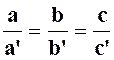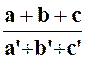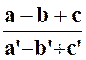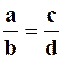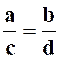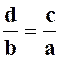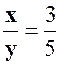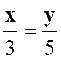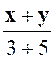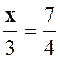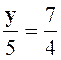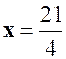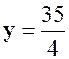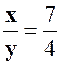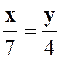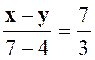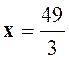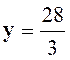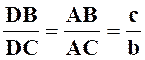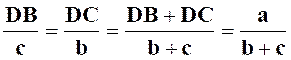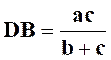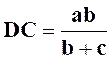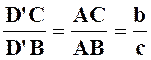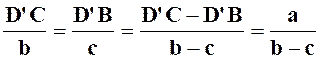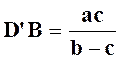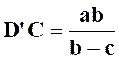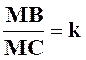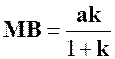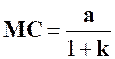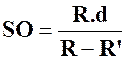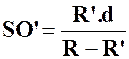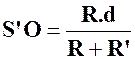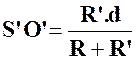COURS :

Info plus.

RAPPORTS :

Le rapport   de « a » à « b » , noté :   , est le nombre « r » par lequel il faudrait multiplier « b »  pour reproduire « a ».

Les égalités

 = r

a = b . r

Sont rigoureusement équivalentes…

Les rapports , qui s’apparentent aux fractions, suivent les mêmes règles opératoires.

Info ++

Théorème des rapports  égaux :

Les égalités :     

Entraînent l’égalité :

                                      avec    étant des facteurs numériques quelconques.

« On obtient un rapport égal aux rapports égaux donnés, en faisant une même  combinaison linéaire sur les numérateurs et les dénominateurs. »                                                

En particulier :

 en traînent   =   =   + …….

Info ++

PROPORTIONS :

Une proportion est l’égalité de deux rapports :

« a » et « d » sont les extrêmes.

« b » et « c » sont les moyens.

Propriétés :

Info 1

Propriété I : Permutation des moyens et des extrêmes.

Si     on a aussi :     et 

Info ++

Propriété II : Produit des extrêmes égal à celui des moyens.                 «  a d =  b c » .

Propriété III : Les proportions participent au théorème des rapports égaux.

3°)   DES EXERCICES TYPES .

Exo 1 : Calculer deux nombres connaissant leur somme « 14 » et leur rapport : «  »

Solution :

«  x + y = 14 »              ( 1 )

                            ( 2 )

De ( 2 ) on déduit ( propriétés I  et III )

  =   = =

 d’où :

Exo  2 : Calculer deux nombres connaissant leur différence  « 7 » et leur rapport : «  »

Indications :

 x  - y = 7

Ecrire :    =   ;        réponse :   et 

Exo 3 : Calculer trois  nombres dont la somme soit « 121 » sachant qu’ils sont proportionnels à :   2 ; 4 et 5 .

Réponses = x = 22 ; y = 44 ; z = 55

4°)   DES PROBLEMES TYPES .

Innombrables sont les applications géométriques ; soit qu’il s’agisse de points partageant un segment dans un rapport donné ; soit de pieds de bissectrices des angles d’un triangle , soit des points en lesquels se coupent sur la ligne des centres des tangentes communes à deux cercles ….

Problème N° 1 : Les trois côtés d’un triangle ont pour longueurs :  BC = a ; CA = b ; AB = c ;  ( b > c ). Les bissectrices de l’angle  coupent le côté «  BC » l’une en « D » ( entre « B » et « C ») L’autre en « D’ » ( en deçà de « B ») Calculer les segment « DB » ; «  DC » ; « D’B » ; « D’C ».

Solution : 

A )  Bissectrice intérieure : point « D ».

Ce point est entre « B » et « C » ,donc :   DB + BC = a       ( 1 )

Mais d’après le théorème de la bissectrice :              ( 2 )                                                                                             

On applique les propriétés  I et III et on tient compte de  ( 1 ) :

       ( 3)

D’où :

B )Bissectrice extérieure : point D’.

Comme on a supposé «  b > c » , les points se suivent dans l’ordre  «  D’BC » et l’on a :   D’C – D’ B = BC = a           ( 5 )

Mais d’après le théorème de la bissectrice :       ( 6 )

On écrit alors ( I  et III ) :

Et les réponses sont :

Problème N° 2 : Un segment  « BC » a pour longueur « a ». Le point « M » situé entre « B » et « C » partage le segment « BC » dans le rapport « k » ( « k » est un nombre positif donné ) . Calculer les longueurs « MB » et  « MC ».

Indications :

Ecrire :

MB + MC = a

Réponses :

 ;                 

Pour l’application  des propriétés I et III  , on a écrit :  au lieu de « k ».

Problème N° 3 : Deux cercles de centres « O » et « O’ », de rayons respectifs «  R »  et  «  R’ »  ( avec  R > R ‘ ) sont extérieures l’un à l’autre. La distance des centres «  O O’ » mesure « d » . Les tangentes communes extérieures coupent le support de « OO’ » en « S » et les tangentes communes intérieures coupent « OO’ » en « S’ » . Calculer les segments  «  SO » ; « SO’ » ; « S’O » ; « S’O’ » .

Réponses :

                ;    ;

                  ;