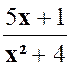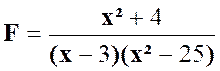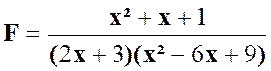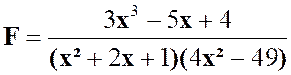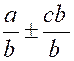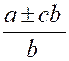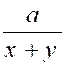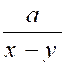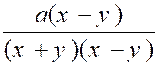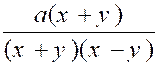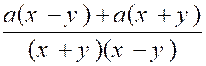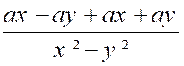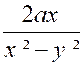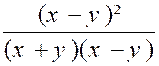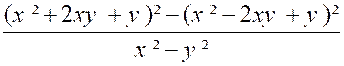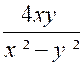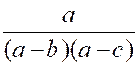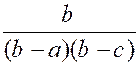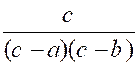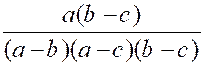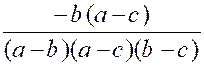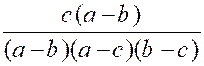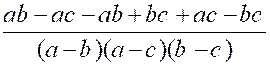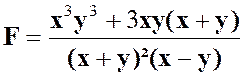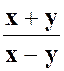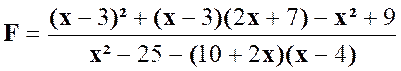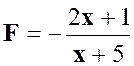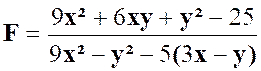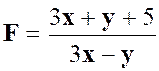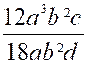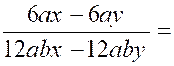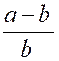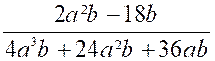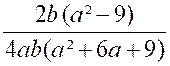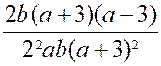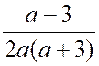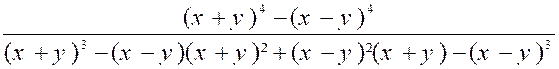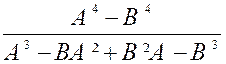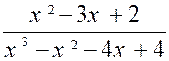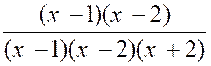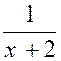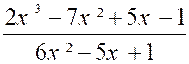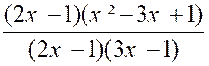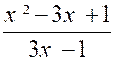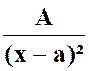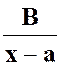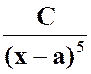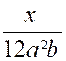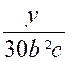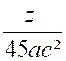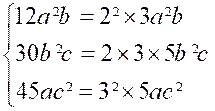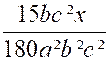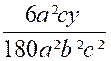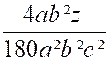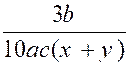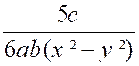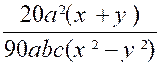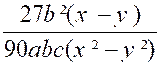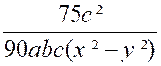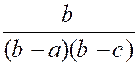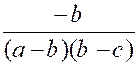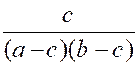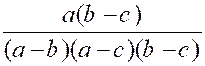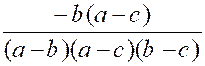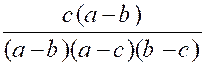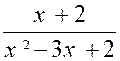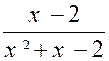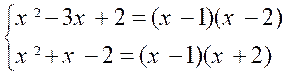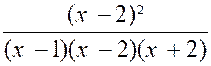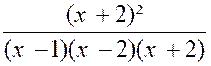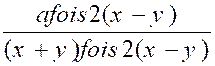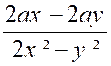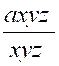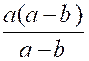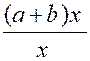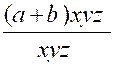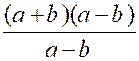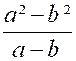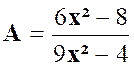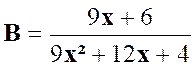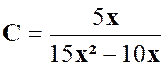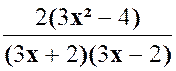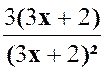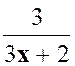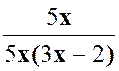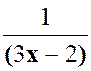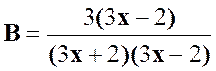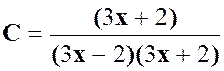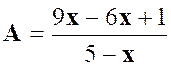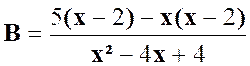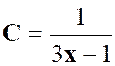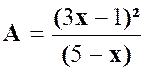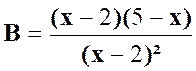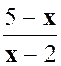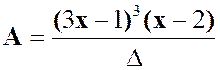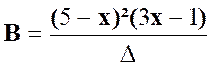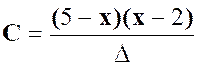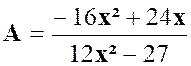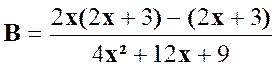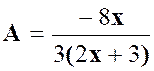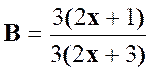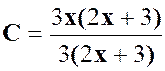la division par zéro n’existe pas dans la fraction…..

Définition.

Propriété fondamentale des fractions.

Egalité de deux fractions.

Décomposition d’une fraction.

Simplification de fraction.

Réduction au même dénominateur  de  fractions.

Une fraction  est l’indication du quotient de deux expressions algébriques.

Info ++

La division par « zéro » étant une opération qui n’existe pas ; il est indispensable que l’expression figurant au dénominateur ( diviseur) ne soit pas et ne puisse pas devenir nulle.

Ainsi étant donné une fraction , il faut s’ assurer que son dénominateur n’est pas nul.et dans le cas où le dénominateur pourrait devenir nul pour certaines valeurs de lettres , il faut « exclure absolument ces valeurs ».

Exemples : 

 ne comporte pas de valeur à exclure ;

  exige l’exclusion de «  x = 5 »

Info ++++

1°) 

Réponse : il faut que l’on ait  ( x – 3 ) ( x² - 25)  0

Ou   ( x – 3 ) ( x + 5 )  ( x -  5 )0

Et les valeurs à exclure sont : x = 3 ; x = + 5 ; x = - 5

2°) 

Indications : il faut que  ( 2 x + 3 ) ( x -3 )²  0

Réponse il faut exclure :  x =  ; et    x = 3

3°)

Réponse : exclure :

« x = 1 » ; « x = » ;   « x  = »

Info +++

Définition :

Une fraction algébrique , ou un rapport algébrique, est l’expression algébrique sous la forme   , du quotient d’une division qui n’a pas été effectuée , que la division soit algébriquement possible  ou non .

Le dividende s’appelle « numérateur » ; le diviseur s’appelle le dénominateur , le numérateur et le dénominateur sont appelés les « termes »   de la fraction.   

Les termes d’une fraction algébrique peuvent être des expressions quelconques , positives  ou négatives , monômes ou polynômes , entières ou fractionnaires , rationnelles ou irrationnelle . Les fractions algébriques sont donc plus générales que les fractions arithmétiques, dont les termes doivent être des nombres entiers et positifs.

On considérera dans les trois premières parties de ce module que les fractions dont le dénominateur est supposé différent de zéro : par la suite la valeur de la fraction considérée sera toujours   déterminée, que la division soit algébriquement possible ou non.

Quand les deux termes sont des polynômes et que la division peut être entreprise , on sait que la fraction  peut se mettre sous la forme d’une quantité « Q » , suivie elle-même d’une fraction ayant pour le reste « r » pour numérateur et le diviseur « b » pour dénominateur tel que :   = Q +

Puisqu’une lettre peut représenter en algèbre une quantité quelconque, si l‘on a une fraction quelconque  , on peut représenter par « q » la valeur bien déterminée du quotient ( complet) quelle représente et écrire  « =q » . Or , en vertu de la définition m^me de la division , le quotient « q » multiplié par le diviseur doit reproduire le dividende .

Donc , l’égalité  « =q » entraîne la relation «  a = b q »

C’est sur l’équivalence entre les égalités « =q » et «  a = b q » que repose toute la théorie des fractions algébriques.  ( 1 )

Remarque : une quantité entière peut se considérer comme une fraction  ayant l’unité pour dénominateur :  « a =  » . cette égalité est conforme à la relation fondamentale :  « =q » car « a fois 1 = a »

Cas des polynômes mixtes :

On entend par « polynôme mixte » un polynôme composé de termes entiers et de termes fractionnaires.

Ainsi un polynôme mixte peut se ramener à une forme entièrement fractionnaire : «  a + b - =  + -  »

Propriété fondamentale des fractions :

Théorème : On n’altère pas  la valeur d’une fraction algébrique en multipliant ou en divisant ses deux termes par une quantité, différente de zéro.

En effet, une fraction algébrique n’est que l’expression d’un quotient

On , on a établi ( dans division algébrique) qu’on n’altère pas la valeur d’un quotient en multipliant ou en divisant le dividende et le diviseur par une même quantité différente de zéro.. Donc ;..

Corollaire : On n’altère pas la valeur d’une fraction en changeant les signes des deux termes , car cela revient à multiplier les deux termes par « -1 »

La valeur de la fraction change de signe , si l’on renverse le signe de l’un seulement des deux termes ; car un quotient change de signe , quand on renverse le signe du dividende seulement ou du diviseur.

Conséquences : la propriété fondamentale des fractions étant la même qu’en arithmétique , les conséquences seront les mêmes : condition d’égalité de deux fractions  , simplification des fractions, réduction au même dénominateur.

Info +++

Egalité de deux fractions.

Théorème : Pour que deux fractions soient égales entres elles , il faut et il suffit que le produit du numérateur de la première par le dénominateur de la seconde soit égal au produit du numérateur d e la seconde par le dénominateur de la première .

Cette condition est nécessaire . En effet , soit « q » la valeur commune des fractions : «  » et «  » : on a les égalités « a = b.q » et « c=d.q » .

Multiplions les deux membres de l’une par « d » et les deux membres de l’autre par « b » : il vient « a d = b.q. d » et « cb =d.q. b ». D’où « ad = cb »

Cette condition est  « suffisante ». En effet , si l’on a « ad = cb » et que l’on divise les deux membres de cette égalité par « bd » , il vient «  =  ; en divisant par « d » les deux termes de la première fraction et par « b » les deux termes de la seconde , on obtient : «  =  » 

Les égalités «  =  »   et «  ad = cb » sont donc équivalentes.

Corollaires :

I ) Pour que deux fractions , dont l’une a un numérateur nul , soient égales , il faut et il suffit que le numérateur de la seconde soit nul également.

Soient les fractions  «  » et «  » . Si , dans l’égalité « ab’ = ba’ »qui exprime l’égalité de ces fractions , on suppose «  a = 0 » , le produit « ab’ » s’annule ; or pour que le produit soit  « ba’ » , dans lequel « b’ » est essentiellement différent de zéro, soit nul aussi , il faut et il suffit que « a’ » soit nul.

II )  Toute fraction dont le numérateur est nul, sans que le dénominateur le soit , est nulle.

En effet, toutes les fractions de la forme «  » sont égales entre  elles, d’après le corollaire précédent ; or , l’une d’elle est la fraction  «  », qui doit être regardée comme égale à son propre numérateur . ( voir remarque ci-dessus « sur a=  » )

Revoir info++

4-  DECOMPOSER UNE  FRACTION :

De même qu’on peut réduire plusieurs fractions en une seule , inversement on peut décomposer une fraction en plusieurs autres.

Exemple :              = ++=  + +

Polynômes mixtes : lorsqu’il se présente des additions ou des soustractions entre termes entiers et termes fractionnaires, on réduit les termes entiers en fractions « équivalentes » ayant pour dénominateurs : le dénominateur commun.

   =        =   

Applications :

N°1 :          + +   =    ++=  

N°2 :   +  =   +

                                      = = =

N°3 :      -   =  -   =   =

N°4 :   +  +   =  ……=    +  +=

=   = 0

Info +++

Simplification des  fractions.

Simplifier une fraction algébrique, c’est lui donner une forme plus simple, mais équivalente.

C’st l’opération qui consiste à modifier l’écriture de la fraction par suppression de facteurs communs aux deux termes de cette fraction.

Règle : Pour simplifier une fraction , on décompose les deux termes en produit de  facteurs et l’on supprime les facteurs communs à ces deux termes.

Le théorème fondamental permet , en effet, de diviser les deux termes par une même quantité.

Par  la suppression de tous les facteurs communs, les deux termes deviennent premiers entre eux : la fraction est dite alors « irréductible » ou « réduite à sa plus simple expression ». 

Marche à suivre :

1°) Décomposer les deux termes en produits de facteurs par application des méthode données dans le cours sur « le produit  algébrique ».

2°) Supprimer les facteurs communs aux deux termes après avoir écrit qu’ils ne sont pas nuls.

Principe :  Etant donné une fraction , on doit toujours, d’abord, se préoccuper de savoir si elle peut être simplifiée.

Série 1 : « simplifier la fraction »

1°)

 ; avec  x  +y  ou  - y

 Le dénominateur est décomposé en produit de facteurs. Occupons-nous du numérateur.

Num. = x ³ +   y ³ + 3 x y ( x + y )

On sait que ( voir : chapitre ) x ³ +   y ³  = ( x + y ) ( x² - x y + y² )

Donc :

Num.= ( x + y ) ( x² - x y + y²  + 3 x y )  =  ( x + y ) ( x²  + 2  x y + y²  )

Num.= ( x + y ) ³ 

Solution :

D’où :  =  ;  pourvu que  ( x + y )  0

2°)

 =

Résumé de la solution :

N = ( x – 3 ) ² + (x – 3 )( 2x – 7 )- ( x² - 9 )

N= ( x – 3) ( 2x + 1)

De même :

D = ( x + 5 ) ( x – 3 )= - ( x + 5 ) ( x – 3 )   avec            x   3  et x   -5

Solution :

          avec            x   3  et x   -5

N°3)

Solution :

 ;  avec  3x + y – 5  0       ; y   3x

Série 2 :

Exemples :

N°1 :  =  = ( le facteur commun est  2 a b² ) 

N°2 :  =

N°3 :  ==

N°4 : = = =

N°5 :     ; posons « x+y=A » et « x-y=B »

Solution :

La fraction proposée devient F = = A + B

En remplaçant les lettres auxiliaires « A » et « B » par leur valeur « x+y » et « x-y »

On a : F = A + B =  « x+y  +  x-y » = 2 x

Remarque : En général , on commence par décomposer le terme qui paraît le plus facile.   Soit :  F=

Commençant par le numérateur , on voit qu’il s’annule pour « x = 1 » ; on le divise par « x-1 » et on a : N = ( x -1)( x - 2)

Le dénominateur à sont tour ,s’annule pour « x=1 » ; on le divise par « x-1 »  et on obtient  D = ( x -1)( x² - 4 ) ; ou D =  ( x -1)( x -2 ) ( x + 2 ) 

D’où :  =    = 

En divisant les deux termes  de la fraction par leur « plus grand commun diviseur » , on la réduit par le fait même à sa plus simple expression ; car les deux termes  deviennent « premier entre eux ».

Par conséquent, lorsque les termes seront des polynômes difficiles à décomposer en facteurs , on cherchera leur « PGCD » , par la méthode des divisions successives , et on les divisera par ce «  PGCD »

Exemple :  =   ; on a pour PGCD : « 2x-1 » d’où  F = = 

Théorème 1 : Toute fraction non identique à zéro est égale à une fraction irréductible.

En effet , on appelle « fraction irréductible » une fraction dont les deux termes sont premiers entre eux. Or en divisant les deux termes de la fraction  proposée par leur « P.G.C.D. » , les quotients sont premiers entre eux .

Théorème 2 : Toute fraction   égale à une fraction irréductible  a ses deux termes équimultiples des deux termes de celle-ci.

En effet l’égalité « = »  donne «  u =  » ; « u » étant entier ;   doit l’être aussi ; or , « b » devant diviser le produit « va » et ne divisant pas le facteur « a » , doit diviser le facteur  « v ». On peut poser « v= bq » : on obtient ainsi  «  u =  » ou «  u = aq ». les deux termes « u » et « v » de la première fraction s’obtiennent donc en multipliant les deux termes « a » et « b » de la seconde par un même facteur.

Info plus.

Réduction au même dénominateur  de  fractions.

Cette opération consiste à modifier l’écriture des fractions données, de façon à leur faire acquérir le même dénominateur.

Comme ci-dessus il faut ,préalablement chercher à simplifier les fractions, les dénominateurs se trouvent être décomposés en produits de facteurs. ( application : ici pré requis et rappels ).

On adopte pour dénominateur commun le produit de tous les facteurs figurant dans les dénominateurs décomposés, s’il y a deux facteurs constitués par la même expression, on adopte l’exposant le plus élevé.

On prendra : comme dénominateur commun :    ( x – a ) ⁵

Le dénominateur commun  étant formé, on multiplie les deux termes de chaque fraction par un multiplicateur tel que l’on fasse acquérir à cette fraction le dénominateur : .

Pour une fraction :   le multiplicateur est l’ensemble des facteurs qui manquent  à «  » pour qu’il devienne «  »…………………..

Règle 1: Pour réduire plusieurs fractions au même dénominateur , sans altérer leur valeur , on multiplie les deux termes de chacune d’elles par le produit des dénominateurs de toutes les autres.

Le théorème fondamental permet , en effet, de multiplier les deux termes d’une fractions par une même quantité .

Exemple : soient les fractions : «  » ; «  » et «  » ; on aura :  « =    » ; «  = » et  «  =  » 

Lorsque les dénominateurs des fractions données ne sont pas premiers entre eux , deux à deux , le dénominateur commun obtenu ne sera pas le plus simple possible . On remplacera , dans ce cas , la règle précédente par la suivante.

Règle 2 : Pour réduire plusieurs fractions au même dénominateur  le plus simple possible , on simplifie les fractions ; puis on forme « le plus petit commun multiple » entre les dénominateurs des fractions simplifiées : on prend ce « P.P.C.M. » pour dénominateur commun et l’on multiplie le numérateur de chaque fraction par les facteurs de ce dénominateur nouveau  qui n’entraient pas dans l’ancien dénominateur de la fraction considérée.

Cette opération revient à multiplier les deux termes de chaque fraction par le quotient obtenu en divisant ce « P.P.C.M. » par le dénominateur de la fraction considérée.

Exemple 1 :

Soient les fractions :  ;  ;

                                   le PPCM =  2² 3² 5 a² b² c² =  180 a² b² c²

On multiplie  « x » par les facteurs « 3 ; 5 ; b ; c² ; » ; puis « y »  par les facteurs «  2 ; 3 ; a² ; c »  et  « z » par les facteurs « 2² ; a ; b² » et l’on obtient :

 ;                       ;               

Exemple  2. Soient les fractions :    ;  ;   ( 1 )

On trouve le nouveau dénominateur commun :  =  2 x 3² x 5 abc ( x + y )( x – y )   =     90 abc ( x² - y² )

Le premier numérateur : on multiplie  « 2a » par « 2 x 5 a ( x + y ) » ;  le deuxième numérateur :   « 3 b » par « 3²b(x – y ) » ; le troisième numérateur « 5c » par « 3x 5c » 

( 1 )  devient :   ;    ;

Exemple 3 : Soient les fractions :  ;   ;

Il semble que les trois dénominateurs n’aient aucun facteur commun et que le plus petit dénominateur commun doive être le produit de six binômes ; mais , si l’on change le signe du facteur ( b- a) et ceux des deux facteurs ( c – a) et ( c – b) ces fractions deviennent :

 ;  ;  ;                    alors   le P.P.C.M. sera ( a – b) ( a – c ) ( b – c )

les fractions deviennent :

 ;       ;    

Exemple 4 : Soient les fractions :   ( F1)      et   ( F2) 

       d’où le p.p.c.m. = ( x- 1) ( x – 2 ) ( x + 2 )

Les fractions deviennent :   ( F1)        ( F2)     ;

Remarques : 

N°1 : En général, on peut « réduire » une fraction à un dénominateur donné , sans altérer la valeur de la fraction , à condition que ce dénominateur  soit un multiple de dénominateur primitif.

Il suffit de multiplier les deux termes de la fraction par les facteurs du dénominateur nouveau qui n’entraient pas dans le dénominateur précédent.

Exemple : soit à donner à la fraction «  » le dénominateur « 2 x²- 2 y² »

L’opération est possible ; car  «  2 x² - 2 y² = 2 ( x + y ) ( x – y ) »  On trouve  = =

N°2 : On peut transformer une quantité entière en une fraction de dénominateur donné : il suffit de multiplier et de diviser à la fois cette quantité par le dénominateur donné.

Exemple : Soit à réduire « a » aux dénominateurs « x » ; « xyz » ; « a-b » ; on aura :

 ;  ;

De même , soit la quantité «  a+b » ; il viendra :  ;  ;   ou

N°3 : La réduction des fractions au même dénominateur permet :

de ranger , par ordre de grandeur , des fractions données et d’étendre aux fractions les principes relatifs aux inégalités.

D’addition ou de soustraire des fractions (possible que si les dénominateur sont identiques)

Autres séries d’exemples : (niveau 4)

Réduire au même dénominateur les fractions suivantes :

Exercice N°1

   ;             ;        

Solution :

La fraction « A »

  devient :       avec            x     et x    ; elle ne se simplifie pas….

La fraction « B »:

  devient :     =     avec x  

La fraction « C »:

   devient :    = 

Constat : le dénominateur commun est :  = ( 3 x + 2 ) ( 3 x – 2 ) ;

Seul le dénominateur de la fraction « A » n’est pas modifié :

Pour « B » le multiplicateur est ( 3 x – 2 )

=

Pour « C » le multiplicateur est ( 3 x + 2 )

 =    

Exercice N°2

Réduire au même dénominateur les fractions suivantes :

    ;             ;        

Solution (développement ) :

               avec x  5

    =            avec x  2

                   avec x  

On en déduit le dénominateur commun :   = ( 5 – x ) ( x – 2 ) ( 3 x – 1 )

Solution finale :

    ;   ; 

Exercice N°3

Réduire au même dénominateur les fractions suivantes :

      ;  ;

Réponses :

   ;  ;          avec x   et    avec x

Info  (1)

Un fraction arithmétique  est une expression qui indique combien une quantité renferme de parties de l’unité divisée en parties égales.

Partant de cette définition , on montre , en arithmétique, que toute fraction multipliée par son diviseur  reproduit son dividende . ( exemple :  x 11 = 3 ) et , par suite, peut se considérer aussi comme l’expression d’un quotient .

Le rapport arithmétique «  » de deux grandeurs « A » et « B » est le nombre qui mesure la première « A » quand on prend la seconde « B » pour unité.

Partant de cette définition , on montre que le rapport «  »est aussi le quotient de la division des nombres qui mesurent les grandeurs « A » et « B » quand on prend une même unité de mesure : appelant « q » cette commune unité , on a  « A= aq » et « B= bq » et l’on en déduit que «  =  »

Aussi , pour la fraction arithmétique et pour le rapport arithmétique  la propriété « x b = a »  ou l’équivalence entre les écritures « =q » et  « a= bq » est une conséquence de leurs définitions, tandis que cette propriété constitue  la définition même de la « fraction algébrique » .

La fraction algébrique diffère donc de la fraction arithmétique et du rapport arithmétique non seulement  par sa généralité , mais par sa définition ; cependant elle les contient l’un et l’autre comme le général contient le particulier . Il n’est donc pas superflu de démontrer directement les propriétés des fractions algébriques  et les règles qu’elles suivent dans les calculs.

Refaire les exercices du cours….

1°)   Quel valeur exclure pour :

;

 :  

Réponse : il faut que l’on ait  ( x – 3 ) ( x² - 25)  0

Ou   ( x – 3 ) ( x + 5 )  ( x -  5 )0

Et les valeurs à exclure sont : x = 3 ; x = + 5 ; x = - 5

1°) 

Réponse : il faut que l’on ait  ( x – 3 ) ( x² - 25)  0

Ou   ( x – 3 ) ( x + 5 )  ( x -  5 )0

Et les valeurs à exclure sont : x = 3 ; x = + 5 ; x = - 5

2°) 

Indications : il faut que  ( 2 x + 3 ) ( x -3 )²  0

Réponse il faut exclure :  x =  ; et    x = 3

3°)

Réponse : exclure :

« x = 1 » ; « x = » ;   « x  = »