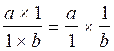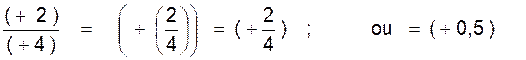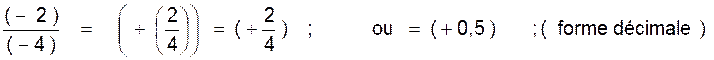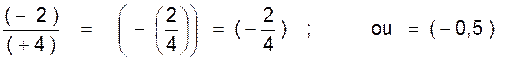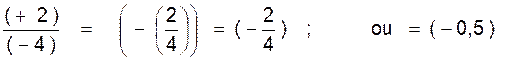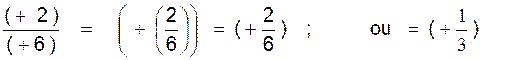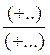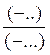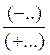Rappels .

( Recherche du quotient décimal relatif )

REGLES concernant la division de deux nombres relatifs .

Traduction  des règles en modèles mathématiques .

Rappels essentiels :

   I )   « la valeur absolue » est la valeur arithmétique du nombre relatif.

 II  )  Se souvenir qu ’ à chaque fois que l’on fait un calcul avec deux nombres relatifs on recherche un troisième nombre relatif  dont on devra rechercher :

                            sa valeur absolue et son signe.

III)  DIVISION :

     Le quotient   « a : b » est le résultat d’une division(de deux nombres )

IV ) On dit aussi que la division peut se transformer en multiplication.

Voir « la fraction : @  nomenclature »

Démonstration :

  nous savons que      a : b  s’écrit             et       que       « l’inverse de b »   s’écrit 

  Nous pouvons  écrire que   est égal a la multiplication     

puisque    est égal  à  inv.b    on peut écrire que    =  a  inv.b

 Nous pouvons dire que : La division est égal au produit  dividende par l’inverse du diviseur .

    On ne traite que deux nombres à la fois

V) Pour comprendre ce qu’est un nombre relatif se souvenir qu ‘un nombre négatif   représente de « l’argent dû » (une dette ; de l’argent en « moins » ) et qu’un nombre positif représente une « rentrée d’argent ». (de l’argent en « plus »)

INFO COURS : sur la division de deux nombres relatifs.

Pour diviser des nombres relatifs , on applique les  mêmes règles , en   remplaçant  le signe de a multiplication  par celui de la division.

REGLES concernant la division de deux nombres relatifs :

Il existe  2  cas : les deux nombres sont de même signe ou les deux nombres sont de signe contraire ( ou opposés)

Remarque :

Si le quotient des valeurs absolues n’est pas exact alors on exprime le résultat sous forme d’une fraction simplifiée ou irréductible !!

Exemple :

La division ne tombe pas juste , on pourrait donner un résultat   sous forme   arrondie   =   ( + 0,3333….)    ou simplifiée    =  0,33     à 0,01 prés

La bonne réponse dépendra de la consigne donnée.

On nous  demandera un résultat sous forme « simplifiée «  irréductible » ou « arrondi » ;…………… 

TRAVAUX Auto- FORMATIFS.

CONTROLE:

     1.  Qu’obtient-on lorsque l’on divise deux nombres relatifs ,préciser ?

     2. Citer les deux règles concernant la division de deux nombres relatifs:

               a) Lorsque les deux nombres sont de même signe.( + et  +  ; - et -  )

               b) Lorsque les deux nombres ne sont pas de même signe ( on dit aussi « signe contraire »)

     3.  Transcrire en langage mathématique  les règles précédentes. ( indication :il y a 4 cas)

EVALUATION:

Faire les calculs suivants:

A) calculer :

    (+3): (+2) =

    (+3) : (-2) =

    (-3 ) : (+2) =

     (-3)  : (-2) =

B)  calculer :

  (+12,45)   :  (-0 ,25)  =

    ( +  40 )  : ( +8,2)  =

        (-3,5)   :   0      =

       (-12,3)  :  (-1)  =

       (+   29,76 )  :  (- 1,86)  =

 C)  Exprimer le résultat   0.01  prés:

                  (-13) : (+3) =

                    17 : (-7)  =

             (+91) : (+17) =

              (-17)    : ( - 99)  =

On ne peut aller plus loin dans le niveau de difficultés   ( voir les études sur les  FRACTIONS.....)

INTERDISCIPLINARITE