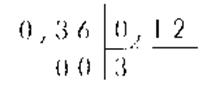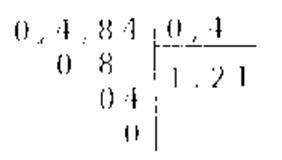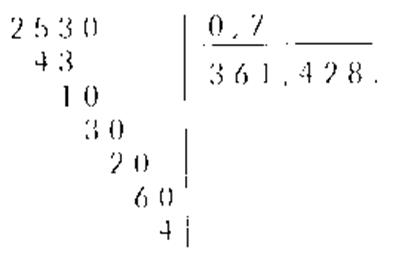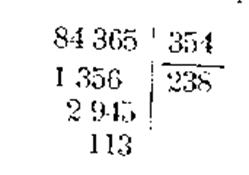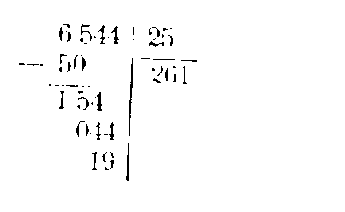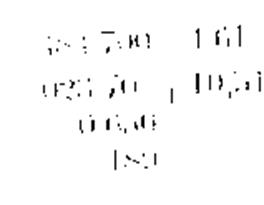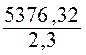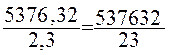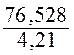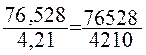Division avec des nombres décimaux

RAPPEL 2

I ) Le résultat de la division est appelé : quotient

Classe 6ème ;		5^ème collège
DOSSIER : LES DECIMAUX non - relatifs / objectif cours 4
		Vers le programme de la classe de 5^ème.

Pré requis:

Savoir établir la table de multiplication d’un nombre entier (au plus 4 chiffres)
Division vue en primaire
Transformer une écriture fractionnaire en fraction
3°) voir la division ( élémentaire)

Et surtout il faut savoir par cœur !! les tables suivantes !

La table des multiplications ( et table de Pythagore)	.
La tableau des divisions.	.

Expression du résultat

A voir : « ARRONDIR » ou « TRONCATURE » (si la division ne tombe pas juste !!!!!)

ENVIRONNEMENT du dossier

Index « warmaths »

Objectif précédent :

Dossier 76 : préparation de la division.

1°) La multiplication dans D

2°) Rappel : division

3°)Division Euclidienne

Objectif suivant

1°) la fraction (nomenclature).

1°) Tableau 47

2°) Activités avec les nombres décimaux

3°) Définitions et activités avec la et les fractions et écritures fractionnaires

2°):les écritures fractionnaires et transformations

3°)approximation

4°) preuve par neuf.

DOSSIER « DIVISION » et « quotients »

Voir l’ objectif @ : >> la Division par 10 ;100 ; 1 000 ; …

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité 1°)division d’un segment

2°) situations problèmes.

Corrigé Contrôle

Corrigé évaluation

Tests :

Série dossier

Si une personne à de réels problèmes pour « diviser » il faut reprendre la feuille de tests ; pour chaque par difficulté une fiche spécifique de formation est proposée. « TESTS divisions@ »

Travaux niveau V :

Révision.

Dos . 116 - 117

A partir du fait que 67 = 42 , on peut écrire 42 : 6 = 7 et 42 : 7 = 6 ;

La division est l’opération inverse de la multiplication : en effet, multiplier puis diviser par un même nombre différent de « 0 » une quantité a un effet neutre sur cette quantité :

Exemple : (13 ) : 2 = 13.

Il est donc évident que savoir faire des divisions passe par la connaissance parfaite des tables de multiplication.

Quand à l’utilisation de la calculatrice pour diviser : l’usage des calculatrices électroniques de poche ne doit pas dispenser de posséder la maîtrise totale des quatre opérations élémentaires :

Addition ; soustraction ; multiplication ; division.

RAPPEL 1

Liens avec: la division dans N ;

PRATIQUE DE LA DIVISION :

PROCEDURE :

exemple diviser 87 par 6

a ) Identifier (nommer)

le dividende : 87

le diviseur : 6

b) établir mentalement (ou par écrit) la table de multiplication dont le nombre « multiplicateur » est le diviseur :

6 1 = 6

62 = 12

63 = 18

64 = 24

65 = 30

66 = 36

67 = 42

68 = 48

69 = 54

c) Poser la division :

d) ) Prendre le premier chiffre du dividende (celui qui appartient à l’ordre le plus grand ici le chiffres « 8 » des dizaines) :

et se poser la question : Dans « 8 » combien peut - il y avoir de fois « 6 » ?

la réponse est dans la table de multiplication :

6 1 = 6

62 = 12

donc 6 1 < 8 < 62 ; « 8 » est compris entre « 6 » et « 12 » ;

en conclure « 8 » contient « 1 » fois « 6 » ; on écrit « 1 » au quotient

1°) On pose la division	commentaires
		8 7	6
	Il y va « 1 » fois « 6 »I		1

e ) Dans la division pratique il faut poser la soustraction 8 - 6 ; et il reste : 2

f ) Il reste « 2 » , j ‘abaisse le « 7 ».

On se pose la question : dans « 27 » combien de fois y a t - il de fois « 6 » ?

On « regarde » dans la table des « 6 » : « 27 » est compris entre 6 _×4 = 24 et 6_×5 = 30

On « met » « 4 » au quotient

On pose la soustraction 27 - 24 = 3

« 3 » est le reste de la division, le calcul de la division peut s’arrêter là parce que le « reste » est inférieur au « diviseur ».( en effet 3 < 6 )

On écrira en résumé : Dividende = diviseur × quotient + reste 87 = 6 × 14 + 3	Modèle
	Dividende	diviseur
		quotient
	reste

- La fraction @ et écriture fractionnaire (transformation d’une écriture fractionnaire en « fraction »

- Numération @ dans D.

A) ENONCE d’un principe de base :

Le quotient de deux nombres décimaux ne change pas si on multiplie ces deux nombres par le même nombre non nul.

Ce principe permet de ramener toutes les divisions dont le diviseur présente une partie décimale à une division dont le diviseur est un entier .

Exemple : soit la division de 0,36 : 0,12 ;

On pose la division sous forme d’écriture fractionnaire la

Est l’on transforme l’écriture fractionnaire en fraction équivalente ( le numérateur et le dénominateur sont des nombres entiers )

= ( q = 3 )

B) Transformer une écriture fractionnaire ; en vue de faire la division

On veut transformer le numérateur et dénominateur ayant des termes décimaux ( exemple: ) par une fraction .(Termes « entiers »)

Procédure:

Pour remplacer une écriture fractionnaire( ) par une fraction équivalente.( ), il suffit de multiplier le numérateur et le dénominateur par 10 ou un multiple de dix . ( ) ;il est possible ensuite de rendre la fraction ,irréductible.

*A prés transformation :le numérateur et le dénominateur doivent contenir le même nombre de chiffres

( en pratique ,il suffit de mettre autant de chiffres au numérateur qu’au dénominateur ,pour cela on rajoute des zéros ,et l’on retire la virgule).

Exercice résolu:

Question : Mettre l’écriture fractionnaire suivante (1,75 / 3,2 ) sous forme de fraction ,ensuite rendre irréductible cette fraction.

Réponse:

Transformer les écritures suivantes en vue de faire la division ,au quotient obtenu à l’unité prés.

654,4 : 2,5 =

84,365 : 0,354 =

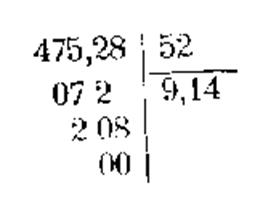
475,28 : 52 =

4 847 : 4,61 =

COURS

Enoncé d’un principe de base :

Le quotient de deux nombres décimaux ne change pas si l’on multiplie ces deux nombres par un même nombre non nul.

Ce principe permet de ramener toutes les divisions dont le diviseur ( et ou le dénominateur ) présente une partie décimale à une division dont le diviseur et dénominateur sont des nombres entiers. ( voir le rappel en début de ce cours )

Exemple :

Calculer 2,34 : 0,24 =

La division de « 2,34 » par « 0,24 » se ramène à celle de « 234 » par « 24 »

Modèle

S’il existe un nombre décimal « q » tel que « a = b q » , ( a ; b Î D , b non nul ) , « q » est appelé « quotient exacte » .

II ) La forme du résultat de la division.(valeur du quotient ; son expression numérique)

Dans le cas où le reste de la division de « a » par « b »n’est pas nul , on ne parle plus de quotient exacte mais de « quotient approché » ou encore « d’approximation décimale »

Exemples de divisions:	Forme du quotient
4,20 : 2,1 =	Un nombre entier	= 2
4,5 : 3 =	Un nombre décimal "fini":	= 1,5
2,1 : 3,2 =		= 0,65625
39,3 : 91,7 =	Un nombre décimal "infini: Le résultat sera une fraction irréductible ou Le résultat sera : soit arrondi ou tronqué (la décision sera soit imposée par la limite de capacité d'affichage de la calculatrice ;ou par un "ordre" fixé.)	= 0,428571428…ou = 3/7

Remarque :

La division « ne tombe pas juste » , on parlera d ‘approximation décimales du quotient :

Dans le cas où le reste de la division de « a » par « b » n’est pas nul , on ne parle plus de « quotient exacte» mais de : quotients approchés par défaut ou encore d’approximation décimales par défaut de ce quotient .

NB : en informatique , l ‘ expression « approximation par défaut » est remplacée par le mot « troncature » ; en abrégé : tronc .

( cliquer ici pour avoir des exemples )

III ) PRATIQUE DE LA DIVISION avec des nombres entiers ( N) dans l ’ ensemble des nombres décimaux ;

Cas 1: le quotient est un nombre décimal (avec une virgule) ; le reste est égal à 0

PROCEDURE :

exemple diviser 87 par 6

a ) Identifier (nommer) : le diviseur et le dividende.

le dividende : 87

le diviseur : 6

b) établir mentalement (ou par écrit) la table de multiplication dont le nombre « multiplicateur » est le diviseur :

6 1 = 6

62 = 12

63 = 18

64 = 24

65 = 30

66 = 36

67 = 42

68 = 48

69 = 54

Dividende

diviseur

87

6

c) Poser la division :

modèle

d )Prendre le premier chiffre du dividende : « 8 » ; le comparer à « 6 » ,

se poser la question : dans « 8 » combien peut - il t avoir de fois « 6 » ?

la réponse est a rechercher dans la table des « 6 » :

6 1 = 6

62 = 12

on remarque que :

87

6

1

« 8 » est compris entre « 6 » et « 12 » ; on peut conclure que « 8 » contient une fois « 6 » ; on écrit « 1 » au quotient

ou plus généralement : Combien « de fois » contient le premier chiffre du dividende le nombre « diviseur » ?

e ) Dans la division pratique il faut poser la soustraction 8 - 6

8 7

6

6 1

- 6

1

2

reste : 2

f ) reste « 2 » , j ‘abaisse le « 7 ».

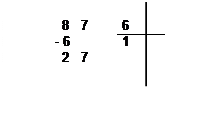
g) le nouveau dividende « vaut » : 27

On se pose la question : dans « 27 » combien de fois y a t - il de fois « 6 » ?

   8 7

6

- 6

14

   2 7

6 4

- 2 4

reste

     0 3

On « regarde » dans la table des « 6 » :

« 27 » est compris entre 64 = 24 et 65 = 30

On « met » « 4 » au quotient

On pose la soustraction 27 - 24 = 3

« 3 » est le reste de la division ( parce que le « reste » est inférieur au « diviseur »)

A ce niveau continu la division dans l’ensemble des nombres décimaux, après la virgule.............

g ) pour que la division puisse se poursuivre il faut :

- ajouter des «un ou plus de « zéro » à la fin du dividende de départ ( 87 00 )

- placer une virgule à la suite du dernier chiffre du quotient « 14 , »

   8 7 0

6

   6

14 ,

   2 7

6 4

- 2 4

   0 3   0

    - descendre   le premier « zéro »

h) et de s’interroger :dans « 30 » combien de fois y a t il « 6 » ? « 65 = 30 »

On place « 5 » au quotient

   8 7 0

6

   6

14 ,5

   2 7

6   4

- 2 4

    0 3 0

65

-      3 0

       0 0

on pose la soustraction « -30 »

j ) le reste étant « zéro » ,la division est terminée

k) Résultat : 87 : 6 = 14 ,5

CAS 2 : le numérateur et (ou ) le dénominateur sont des nombres décimaux ; le quotient est un nombre entier ( N ) (quotient exact)

La division de 0,36 par 0,12 se ramène à celle de 36 par 12

0,36 = 0,12 3 + 0

divOpé4

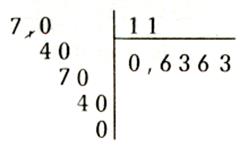
CAS 3 : le numérateur et le dénominateur sont des nombres décimaux ; le quotient est un nombre décimal ( D ) (quotient exact)

Exemples :

divOpé1

divOpé3

CAS 4 : le quotient est un nombre décimal (avec une virgule) ; le reste ne sera pas égal à 0

Exemple :

divOpé2

Si le reste n’est pas égal à « zéro » ; il faut voir l’ objectif : abordant le problème sur « arrondir ....... à ...... « tant prés ».......... » :

Et encore QUELQUES EXEMPLES DE DIVISIONS.........

RESUME sur la PRATIQUE de la division

PROCEDURE pour diviser deux nombres décimaux :

Exemple : Diviser : 5376 , 32 : 2 , 3 jusque 2 chiffres après la virgule ;

1°) mettre la division sous forme d’écriture fractionnaire										5376 , 32 : 2 , 3 =
2°) transformer l’écriture fractionnaire en fraction . ( on multiplie par 100 en haut et en bas , on obtient une fraction équivalente à l’écriture fractionnaire )
3°) poser la division : « euclidienne » On doit diviser un nombre entier « 537632 » par le nombre entier « 3 2 »										5 3 7 6 3 2 ,0 0 ½ 23 ½ --------- ½ ½
Commentaire : Pour effectuer la division, on doit savoir établir « mentalement »la table de multiplication du diviseur « 23 ». Si vous avez des difficultés en calcul mental il est conseiller d’écrire sur la feuille de papier cette table .										0 fois 23 = 0 1 fois 23 = 23 2 fois 23 = 46 3 fois 23 = 69 4 fois 23 = 92 5 fois 23 = 115 6 fois 23 = 138 7 fois 23 = 161 8 fois 23 = 184 9 fois 23 = 207
Division :
		5	3	7	6	3	2	,	0	0		2	3

	-	4	6								2 3 3 7 5 , 3 0
		0	7	7
		-	6	9				On met la virgule au quotient					Pour vérifier ce quotient il faut multiplier : 23 375 , 30 par 23 et ensuite ajouter le reste ; on doit retrouver le nombre : 537632
			0	8	6
			-	6	9
				1	7	3
			-	1	6	1
				0	1	2	2
				-	1	1	5
					0	0	7	,	0
						-	6		9
							0		1	0				Reste 0,1
										0

On conclura : 5376 , 32 : 2 , 3 » 2 3 3 7 5, 3 0 à deux décimales

Exemple 2 : diviser 76,528 : 4,21 , donner le résultat à deux décimales près.

1°) écriture fractionnaire										76,528 : 4,21 =
2°) fraction équivalente :
3°) table de multiplication de « 4210 »										0 fois 4210 = 0 1 fois 4210 = 4210 2 fois 4210 = 8420 3 fois 4210 = 12630 4 fois 4210 = 16 840 5 fois 4210 = 21 050 6 fois 4210 = 25 260 7 fois 4210 = 29 470 8 fois 4210 = 33680 9 fois 4210 = 37 890

Division :
	7	6	5	2	8	,	0	0	0		4	2	1	0
-	4	2	1	0
	3	4	4	2	8						1 8 , 1 7 7
-	3	3	6	8	0
	0	0	7	4	8		0					Pour vérifier ce quotient il faut multiplier : 18,17 7 par 4210 et ensuite ajouter le reste ; 2,83 on doit retrouver le nombre : 76528
		-	4	2	1		0
			3	2	7		0	0
		-	2	9	4		7	0
			0	3	2		3	0	0
			-	2	9		4	7	0
Reste :				0	2	,	8	3	0

						On met la virgule au quotient
												Reste : 2,830

On conclura : 76 , 528 : 4,21 » 18,18 à deux décimales prés

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°) Comment appelle-t-on le résultat de la division?

2°) Quelle peut être le forme du résultat de la division?

EVALUATION :

EXERCICES à faire sur feuille ; vérification ensuite à la calculatrice.

Donner le résultat au 0,01 prés

I ) Effectuer les divisions suivantes :

a	167 : 8	c	753 : 6	d	456 : 7	e	830 : 9
f	256 : 27	g	485 :58	h	849 : 95	i	358 : 24
j	1 694 : 58	k	3 274 :43	l	2 380 :39	m	8 764 :73
n	76 465 :932	p	46 178 :375	q	76 548 :654	r	56 381 : 784

II ) Calculer jusqu ‘aux dixièmes :

a	425 : 4	b	237 : 5
c	807 : 46	d	198 : 27
e	9 087 : 97	f	2 783 : 64
g	54 639 : 499	h	98 569 : 531

III ) Calculer jusqu ‘aux centièmes :

a	831 :7	b	217 : 4
c	573 : 81	d	782 : 97
e	6 781 : 21	f	1470 :18
g	20 682 : 702	h	80 987 : 614

IV ) Calculer jusqu’ aux millièmes :

a	630 : 3	b	427 : 6
c	632 : 19	d	942 : 72
e	4 291 : 27	f	5 431 :86
g	56 045 : 792	h	59 234 : 321

AVEC DES NOMBRES DECIMAUX :

I ) Effectuer les divisions suivantes :

1	34,8 : 22	9	646 ,52 : 932
2	76,4 : 46	10	81 , 786 : 373
3	39,7 : 19	11	638,19 : 784
4	27,8 :58	12	3 ,7654 : 845
5	288 : 2,1	13	7 211 :7, 81
6	627 : 5,6	14	4 560 : 67,5
7	798 : 3,7	15	4 001 : 80,4
8	976 : 4,8	16	8 762 : 5,36

II ) Série2 ; Effectuer les divisions suivantes :

1	62, 7 : 2,7	9	6 515,2 : 4 ,14
2	6, 94 : 6,2	10	746 , 93 : 47 ,1
3	31 ,2 : 2 ,3	11	5 ,7643 : 4 ,28
4	7 ,94 : 2,8	12	95 ,643 : 0 ,428
5	0 , 985 :0, 39	13
6	5 ,61 : 0 ,86	14
7	1 967 ,4 : 7 , 55	15
8	48 , 630 : 4 ,87	16

III ) Série 3 ; Effectuer les divisions suivantes :

1	876 : 300	9	0 , 876 : 3 , 200
2	504 : 450	10	2 : 3 ,84
3	640 : 800	11	9 , 006 : 0 , 178
4	87 300 : 4 000	12	1 , 627 : 0 , 0196
5	45 000 :6 050	13
6	70 800 : 9 000	14
7	79 , 8 : 720	15
8	6 , 54 : 3 000	16