"Pré requis:
|
|
ENVIRONNEMENT du dossier:
|
|
|
|
|
|
|
|
|
|
|
Objectif précédent |
|
|
COURS |
Devoir
Contrôle |
Devoir évaluation |
|
PREUVE
PAR "9" des 4 OPERATIONS
Addition ; soustraction ; multiplication ; division
I
) Calcul d'un "reste par 9 "
d'un nombre : (exemple :calcul du reste par 9 de 354 )
|
Nombres |
On addition les 2 premiers chiffres |
On addition au résultat précédent le troisième chiffre;
ainsi de suite |
Au dernier résultat, si il contient 2 chiffres on
additionne ces deux chiffres pour obtenir le résultat |
|
10 |
1+0 =1 |
|
1 |
|
134 |
1+3 =4 |
4+4 =8 soit ( 1+3+4 = 8) |
8 |
|
354 |
3+5 = 8 |
8+4 = 12 soit 3+5+4= 12 |
1+2 =
3 |
|
5627 |
5+6 = 11 ; 11 +2 =13 ;13+7 =25 soit 5+6+2+7 = 25 |
2+5
= 7 |
|
|
75,683 |
7+5=12+6 =18+8=26 ;26+3 =29 soit : 7+5+6+8+3 |
2+9=11=
2 |
|
|
|
|
|
|
|
Remarque
: le "+ 9" |
Peut
être assimilé |
à
"+ 0" |
|
|
|
|
|
|
|
Exemple: 9 + 4 donne 4 |
En effet: 9 + 4 = 13
|
Et 13 donne 1+3 =4 |
Donc = 9 +7
donne 7 9 + 3 donne
3 |
ADDITION: et la preuve par
"9"
354 3+5=8 8+4 =12 1+2 = 3 + 718 7+1 = 8 8 + 8 =
16 1+ 6 =
7 1072
On a obtenu les
"restes par 9 " 3 et 7
On additionne ces restes
et on calcule le reste par 9 de leur somme
:
7+3 =10
; 1+0 = 1
La somme de l'addition est
bonne si l'on obtient le même résultat en
additionnant les chiffres du nombre "somme = 1072 "
Calcul
du reste par 9 de 1072
: 1+0 = 1 ; 1 +7 = 8 ; 8+ 2 = 10 ; 1+0
= 1
Conclusion : on obtient
le même résultat les restes par 9 sont égaux
, on peut affirmer que 1072 est la somme des nombres 354 et 718.
SOUSTRACTION : et
la preuve par "9"
Pour faire la preuve par
9 de la soustraction ;on procède comme pour l'addition :
|
7 1 8 |
7 + 1 = 8 |
8 + 8 = 16 |
1 + 6 = 7 |
|
-
3 5 4 |
3
+ 5 = 8 |
8 + 4 =12 |
1+2 = 3 |
|
3 6 4 |
|
|
|
On a obtenu les
"restes par 9 " 3 et 7
On soustrait ces restes
et on calcule le reste par 9 de leur somme différence :
7- 3 =4 ; 4
La différence de la
soustraction est bonne si l'on obtient le même résultat en additionnant les chiffres du nombre
"différence = 364 "
Calcul
du reste par 9 de 364
: 3+6 = 9 ; 9 +4 = 13 ; 1+ 3 = 4
Conclusion : on
obtient le même résultat les restes par 9 sont égaux , on peut affirmer que 354 est la différence
entre les nombres 354 et 718.
Autrement :on fait reste + petit nombre = grand nombre
364 + 354
= 718
avec les restes par 9 cela devient:
4 + 3
= 7
7 =
7 conclusion: les restes par 9
sont égaux
MULTIPLICATION: et la preuve par "9"
Travail
: faire la vérification de 646 
328 = ? = 211 888
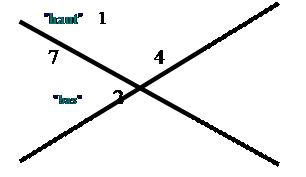
On identifie Calculs des "restes par 9" Multiplicande : 646 6+4+6 = 16 ;1 +6 = 7 ; reste 7 Multiplicateur
328 3+2+8 = 13 ; 1+3 = 4 ;reste 4 Produit des restes 7 et 4 7 fois4 = 28 ; 2+8 = 10 ; 1+0 = 1 reste 1 Reste par 9 du produit 211888 2+1+1+8+8+8 =28 ; 2+8 =10 ; 1+0 = 1 ; reste 1 On compare les "restes" du produit des
"reste" et reste du produit de la multiplication : on a
"1" et "1" conclusion :ils sont égaux ! le produit est "bon"
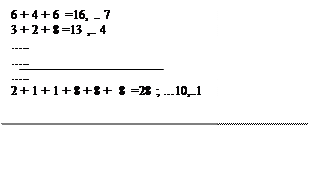
Conclusion :
Pour que le produit ( ici
211 888 )soit considéré comme exact on doit obtenir le même résultat
dans les cases opposées du "haut" et du "bas" de la croix.
(ce qui est le cas on peut dire que 646 328 = 211 888 )
DIVISION: : et la preuve par "9"
Pour faire la preuve par 9
de la division , on doit tenir compte du reste (si le quotient n'est pas
exact).
|
Voir
division euclidienne |
On doit vérifier les deux opérations: (système)
( 1 ) Diviseur quotient = produit et ( 2 ) produit + reste = dividende
cela ce présente comme la croix
qui suit : divisons 13426 : 23 = ?
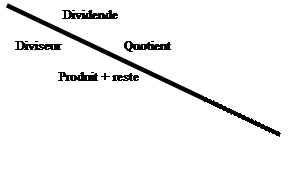
On demande de vérifier le résultat suivant :
13 426 : 23 = 583 reste 17
On identifie: Calculs des
"reste par 9" Diviseur : 23 2+3 = 5 Reste
= 5 Quotient : 583 5+8+3 = 16
Reste = 7 Produit: 5 3+5 = 8 ;
reste = 8 Reste =
17 1+7 = 8 ; reste = 8 Produit +reste : 8+8 =16 1+6 = 7 ; reste = 7 Dividende 13 426 1+3+4+2+6= 16 ; 1+6 =7;reste = 7
7 =35
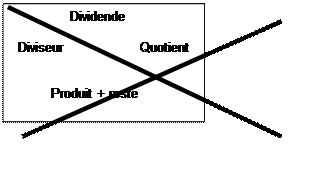
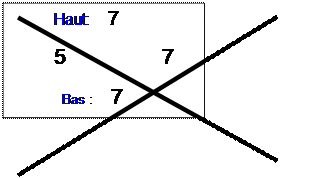
Conclusion : On doit obtenir le
même résultat dans les cases
opposées du "haut" et du "bas" de la croix.
1)Que signifie l' expression :
"calculer le reste par 9" , donner plusieurs exemples.
2)Comment procède - t - on pour
effectuer la preuve par neuf d'une : addition ?
3) Comment procède
- t - on pour effectuer la preuve par
neuf d'une : soustraction ?
4) Comment procède
- t - on pour effectuer la preuve par
neuf d'une : multiplication ?
5) Comment procède
- t - on pour effectuer la preuve par
neuf d'une :division ?
EVALUATION :
I ) Faire le
calcul d'un "reste par 9 " des nombres suivants :
|
|
Calculs successifs |
le résultat |
|
|
10 |
|
|
|
|
134 |
|
|
|
|
354 |
|
|
|
|
5627 |
|
|
|
|
75,683 |
|
|
|
2 ° ) Faire la preuve
par neuf des opérations suivantes Lentourez le bon résultat en justifiant par la preuve par
9)
|
|
Propositions. |
|
354 + 718 = |
1072 ou
1062 |
|
718 - 354 = |
334 ou
364 |
|
646 |
211 888
ou 212868 |
|
13 426 : 23 = |
581 reste 17 ou 583 reste 17 |
CORRIGE EVALUATION :
I ) Faire le calcul d'un
"reste par 9 " des nombres suivants
:
|
|
|
|
le
résultat |
|
10 |
1+0 =1 |
|
1 |
|
134 |
1+3 =4 |
4+4 =8 |
8 |
|
354 |
3+5 = 8 |
8+4 = 12 |
1+2 = 3 |
|
5627 |
5+6 = 11 +2 =13 |
13+7 =25 |
2+5 = 7 |
|
75,683 |
7+5=12+6 =18+8=26 |
26+3 =29 |
2+9=11= 2 |
2 ° ) Faire la preuve par neuf des opérations
suivantes Lentourez le bon résultat en justifiant par la
preuve par 9)
|
354 + 718 = |
1072 ou
1062 |
|
718 - 354 = |
334 ou
364 |
|
646 |
211 888 ou 212868 |
|
13 426 : 23 = |
581 reste 17 ou 583 reste 17 |
|
|
|