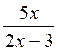|
OBJECTIFS :(concept :fraction; notions de base) : Savoir définir ;identifier et reconnaître ;simplifier une fraction |
I ) Pré
requis:
|
|
|
|
Information sur la
division par zéro !!! |
|
|
|
|
|
"arrondir " ou "troncature" |
II ) ENVIRONNEMENT du dossier :
III ) LECON n° C.N.6 :
LA FRACTION : NOMENCLATURE et lecture .
Chapitres :
|
I )
Préambule: première
série de définitions : « fraction » ;
« rationnel » ; « écriture fractionnaire » ;
« nombre fractionnaire » ; « nombre complexe » |
¥ |
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
IV)
INFORMATIONS « formation
leçon » :
|
Travaux auto - formation. |
|
|
Corrigé des travaux
auto - formation. |
||||
|
Contrôle |
évaluation |
|
|||||
|
|
|
Travaux niv
VI et V en lien avec ce cours : |
|
|
|
|
|
|
|
Dos.138-139
|
|
|
|
|
||
|
Devoir diagnostique L tests. |
|
|
|
|
|
Devoir Formatif « Contrôle :
savoir » ; ( remédiation) |
|
|
|
|
|
Devoir sommatif . |
|
|
Devoir certificatif : ( remédiation ) |
|
* remédiation : ces
documents peuvent être réutilisés ( tout ou partie)
pour conclure une formation .
|
Titre |
|
|
N°C.N.6 |
CHAPITRES
|
I )
Préambule: Première série de définitions :
« fraction » ; « rationnel » ; « écriture
fractionnaire » ; « nombre fractionnaire » ;
« nombre complexe » |
¥ |
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
|
|
¥ |
FRACTION:
Une fraction est le rapport (une division )d’un
nombre entier naturel par un autre nombre entier naturel (exemple :
)
RATIONNEL: Un
rationnel est le quotient d’un entier par un entier non nul.
Exemple:
16 : 2 = 9
9 est un rationnel ( remarquez que « 9 » est un nombre entier)
25: 4 = 6,25 6,25 est un rationnel ( remarquez que « 6,25 » est un nombre entier)
11 : 7 =
11/7 
est un rationnel (( remarquez
que « » n’est ni un nombre entier , ni un nombre
décimal ;et l’on ne peut pas donner la valeur décimale du quotient de la division de 11 par 7 ; donc la fraction
est un nombre
dit « rationnel » ; dans la vie courante certaines personnes
donneront une valeur décimale arrondie à
la valeur numérique du
quotient , en disant que
11 /7 est égal à « 1,5714286 »
pour la calculatrice de collège ;
et un ordinateur donnerait la valeur suivante
«1,57142857142857142857142857142857 ……..» par ce que la division ne tombe pas
juste » )
Ecriture fractionnaire: On appelle écriture
fractionnaire le rapport de deux nombres
non entiers.(au plus le numérateur et le dénominateur sont des nombres décimaux)
(Exemples 
; 
; 
;
)
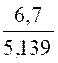Nombre fractionnaire : ( info @ + dos.
148)
On appelle nombre fractionnaire
un nombre entier associé à une fraction ,
séparé par un point . exemple
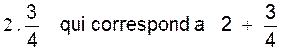
Nombre complexe : en arithmétique on appelle « nombre complexe » les nombres qui exprime les unités d’heures et d’angles.
Pour mesurer
« la durée » on utilise
l’unité « heure » ; cette
unité est découpée en 60 parties
appelées « minute » et l’unité de minute est découpée 60 parties appelées « seconde »
L’unité mesurer un angle on utilise l’unité « degré », cette unité est découpée en 60 parties appelées « minute » et l’unité de minute est découpée 60 parties appelées
« seconde » ( info @ + dos.
169)
Dos.138-139
|
II ) Définition
|
¥
|
Eléments
concrets :
souvent au lieu de calculer avec des nombres
entiers ou décimaux , nous avons à travailler sur des
unités partagées en 2 ; 3 ; 4 ; 5 ; 6 ; ….. ;8 ;… ;
10 parts égales.
Ainsi nous
pouvons diviser une tableau de chocolat , une pomme ,
une poire , une orange un gâteau , une baguette de pain ; le contenu d’un
plat ; en deux , trois
ou quatre ou plus part égales .Ces parties sont appelés des fractions .
Par définition :
On appelle une
« fraction » une ou
plusieurs parties de l’unité divisée en parties égales .
|
Exemples :
la moitié d’une pomme , le tiers d’un gâteau ; le
quart d’une somme d’argent .
Une fraction est le rapport (une division )d’un nombre entier
naturel ( N ) par un autre nombre entier
naturel (N) (exemple : 3 sur 4 s’écrit
3 sur 4 s’écrit 
)
Commentaire : Il y a les fractions réductibles et
les fractions dites irréductibles ;les
fractions réductibles sont simplifiables.
Dos.138-139
|
¥ |
ou comment reconnaître une
fraction ? (ou une écriture
fractionnaire):
Une fraction ordinaire se compose de deux
nombres ( termes)
superposés ,séparés par un trait horizontal.
Le
nombre supérieur est appelé « numérateur », il indique combien on a
pris de parties de l’unité fractionnée ( divisée en
fractions égales).Le nombre inférieur s’appelle le
« dénominateur » ; il indique en combien de parties l’unité a été divisée , et il donne son nom à la
fraction.
Une fraction se reconnaît à son
écriture mathématique ;elle associe trois
éléments caractéristiques :
Qui sont : deux
nombres entiers ( N ) sont séparés(en
lecture verticale) par une barre horizontale.
Exemple d’écriture
symbolique mathématique :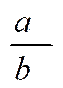 
Lire
:
« fraction « « a » sur « b » »
|
|
¥ |
1°) « a »
est le numérateur. ( c’ est un nombre entier ! lu comme étant la partie entière d’un
nombre décimal).
2°)
« ___ » le trait horizontal est la barre de fraction ; (elle est tracée sur la ligne
d’écriture) ; ce trait horizontal
séparant le numérateur du dénominateur
3°)
« b » est le
dénominateur (important :le dénominateur ne doit jamais être égal à zéro) : c’ est ,aussi , un nombre entier ! lu
comme étant la partie décimale d’un nombre décimal).
|
¥ |
On associe toujours la fraction
à l’opération « division »
dont le dividende s’appelle « numérateur » et le diviseur
s’appelle « dénominateur ».
On peut parfois remplacer
une fraction par un nombre entier , un nombre décimal ou une fraction irréductible ( appelé : le quotient s’appelle :
« rationnel ») .
Le quotient est
obtenu en divisant le numérateur par son dénominateur. si le quotient ne peut
être entier ou décimal (si le reste ne peut pas être égal à zéro) , on laisse ce quotient sous la forme d’une fraction dite
irréductible.
(ce qui
peut-être
intéressant :
le résultat de la
division est utilisé pour classer des fractions entre elles).
|
VI ) Valeur décimale d’une fraction et fraction décimale : |
¥ |
Lorsque le dénominateur d’une fraction
est 10 ; 100 ; 1000 ; …., nous avons ce que l’on appelle une
fraction
décimale , qui peut s’écrire de deux manières :
; 
; 
; 
peuvent s’écrire 0,7 ; 0,23 ; 0,367 ; 0,4563
.
|
¥ |
La fraction « deux
tiers » s’écrit : 
; le numérateur indique que l’on a pris deux
parties . Le dénominateur « 3 » montre que l’unité a été divisée en
trois parties égales .
Pour nommer une fraction on nomme
d’abord le numérateur puis le dénominateur que l’on fait suivre de la
terminaison ième
Exemple :
se lit « sept
huitièmes » ou 
se lit « quatre
neuvièmes »
Si « b » vaut
« 2 » ; lire : « demi » exemple :
l’écriture 
se lit « trois demi »
Si « b » vaut «3 » ; lire :
« tiers » exemple : l’écriture 
: se lit
« deux tiers »
Si « b » vaut
« 4 » ; lire : «quart » exemple :
l’écriture : se lit « trois
quarts »
Si « b » vaut
« 5 » ; lire : « cinquième » exemple : l’écriture 
: se lit
« trois cinquièmes »
Si « b » vaut
« 6 » ; lire : « sixième » exemple : l’écriture 
: se lit « trois sixièmes»
Si « b » vaut
« 7 » ; lire : « septième » exemple : l’écriture 
: se lit
« trois septièmes»
Si « b » vaut
« 14 » ; lire : « quatorzième » exemple : l’écriture 
: se lit
«trois quatorzièmes »
Si « b » vaut « 123
» ; lire : «cent vingt troisièmes » exemple : l’écriture 
: se lit
« trois cent vingt troisièmes »
et
ainsi de suite
.................................................................
Ainsi les fractions suivantes seront
lues :
lire : cinq treizièmes ; 
; lire : deux tiers ; 
;lire :
quatorze cent dixièmes ; 
; trois quart ; 
lire : cinq cent deux cinq cent vingtièmes .
|
|
¥ |
On
retiendra : Lorsqu'une écriture fractionnaire contient
une lettre au dénominateur ('appelée :inconnue ; généralement
"x"" ) il faut
trouver la valeur de "x" qui
doit être exclue , afin de ne pas
avoir la valeur zéro:
Exemples:
|
Soit les
écritures fractionnaires suivantes : |
Commentaire : |
|
|
Pour
effectuer un calcul
;il faut donner une valeur à "x", toutes les valeurs
sont possibles sauf "0" |
|
|
Pour
effectuer un calcul
;il faut donner une valeur à "x", toutes les valeurs
sont possible sauf "0" ; 2 fois 0 = 0 Zéro
est l 'élément
absorbant : |
|
|
Un
calcul est possible sauf si x+1 =0 ; Il
faut calculer (résoudre)pour connaître quelle est la valeur de "x" qui donne "_"+1 =0 On
trouve x = -1 ;
si x=-1 ;alors (-1) +1 =0 Conclusion:
un calcul est possible avec toutes les valeurs de "x" sauf "x = -1" |
|
|
Est
exclue la valeur de "x = 1,5" |
Remarque : la valeur de « x » au
dénominateur ne valoir « 0 »
Pour comprendre on réalisera l’ Activité suivante , avec la calculatrice
, mais importante:
L’objectif des calculs est de vous
montrer ce qui se passe lorsque l’on divise le plus petit nombre entier 1 par un
nombre inférieur à 1 , c'est-à-dire qui commence par
le « zéro virgule….. »
soit 0 ,........1. , on place des « 0 » entre la
virgule et le « 1 » .On dit
que : plus
le chiffre « 1 » recul plus la valeur du nombre tend vers zéro.)
Exemples : Utiliser la calculatrice pour calculer :
1 divisé
par 1
= ; noter le résultat ;..............................................................
1 divisé par
0.1 = ; noter le résultat
;.................................................................
1 divisé par
0.01= ; noter le résultat
;...............................................................
1 divisé par 0.001= ; noter le résultat ;
.............................................................
1 divisé par 0.000001 = ;
noter le résultat;......................................................
;
après avoir
noté le résultat .de chaque
opération on peut conclure
« que plus un nombre est divisé par un autre qui tend vers zéro ,plus le résultat devient grand
.On dira que
le résultat tendra vers un nombre infiniment grand (en valeur absolue)
on doit
conclure : on ne peut donc diviser par « zéro ».
|
¥ |
|
|
Si "a " et
"b" désignent deux entiers , le nombre
obtenu à partir du quotient de "a" et "b" s' appelle un nombre rationnel , ou plus
simplement "un rationnel".
Un rationnel écrit
grâce au signe de division , "a" :"b"
se lit "a" divisé par "b" ; mais il est pratiquement
toujours écrit avec une barre de fraction , a / b , ou 
et se lit "a sur b".
On obtient un rationnel
chaque fois que l' on constitue un quotient d '
entiers , ce quotient est toujours calculable en fraction , parfois en décimal.
Une écriture décimale infinie où se reproduit
infiniment la même séquence de chiffres "cache" un rationnel..
|
Info
@ Elément neutre ! |
¥ |
(il y en a trois)
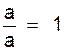Attention : « a » doit
être différent de zéro.
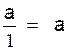dans
ce cas
« 1 » est un élément neutre
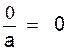Attention : « a » doit
être différent de zéro.
On se rappellera que :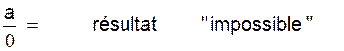 
|
Leçon |
LA FRACTION : NOMENCLATURE et lecture . |
|
N°6 |
TRAVAUX
d ’ AUTO - FORMATION |
1 ) Donnez la définition d’une fraction (caractéristiques).
2 ) Donnez la définition d’un rationnel.
3 ) Donnez la définition d’une
écriture fractionnaire.
4 ) Dites ce que vous savez sur l ’
écriture suivante :
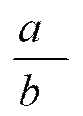
5 ) Compléter les égalités suivantes :
( la lettre « a » représente un nombre entier )
(Dans un des cas il faudra préciser si il y a une
condition particulière)
=
=
=
6 ) Que se passe - t il si on divise le numérateur
par un nombre qui tend vers zéro ?
1
)
Quelle différence y a t - il entre ces
deux écritures 
et 
?
.
2
)
Comment appelle-t-on cette écriture mathématique 
et (nommez tous les
éléments qui la composent) ?
3
)
Traduire en langage littéral :
4
)
En combien de parties faut - il diviser
l ‘ unité pour avoir :
|
des
tiers ? |
|
|
des
seizièmes ? |
|
|
de
quarts ? |
|
|
des
millièmes ? |
|
5
) Lire les fractions suivantes :
|
|
......................................................................... |
|
|
......................................................................... |
|
|
......................................................................... |
|
|
......................................................................... |
|
|
......................................................................... |
6
)
On considère qu ‘une année compte 365 jours.
Quelle
fraction de l’année représente ?
|
5 jours ? |
|
|
30 jours ? |
|
|
265 jours ? |
|
|
360 jours ? |
|
7
)
Quelle fraction d ‘heure représente :
|
10 minutes ? |
|
|
20 minutes ? |
|
|
30 minutes ? |
|
|
45 minutes ? |
|
|
50 minutes ? |
|
8 ) Quelle fraction de la semaine représente :
|
4 jours ? |
|
|
3 jours ? |
|