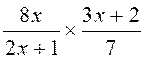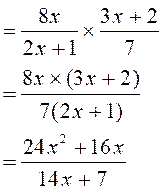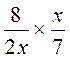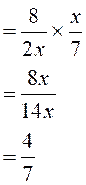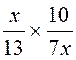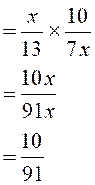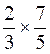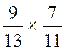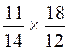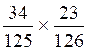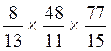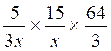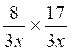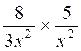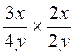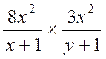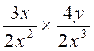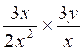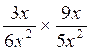Pré requis :
Expression d' un
résultat
|
||
|
|
||
ENVIRONNEMENT du
dossier :
|
Voir la liste des cours sur
les fractions.. |
DOSSIER MULTIPLICATION de deux fractions de dénominateurs différents.
|
TEST |
COURS |
Interdisciplinarité |
|
Définition
de l'objectif: exemple
de multiplication de deux fractions ayant des dénominateurs différents :
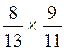
La multiplication de
deux fractions n’ayant pas le même dénominateur se fait
sans difficulté particulière.
A SAVOIR:
|
La
multiplication de deux fractions de dénominateur
différent est égale à une troisième fraction qui aura pour: Numérateur le
produit des numérateurs et pour Dénominateur le produit des dénominateurs. |
Modèle mathématique: 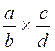 =
= 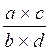 =
= ![]()
Procédure permettant de multiplier des fractions de dénominateur
différent:
1°) Construire une égalité (voir objectif: EG 1) dont le premier membre est l’énoncé (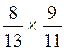 ) et le deuxième
membre est la fraction dont le numérateur sera le produit des numérateurs des fractions
du premier membre et le dénominateur le produit des dénominateurs (
) et le deuxième
membre est la fraction dont le numérateur sera le produit des numérateurs des fractions
du premier membre et le dénominateur le produit des dénominateurs (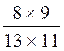 )
)
soit 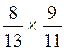 =
= 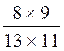
2°) Effectuer la multiplication des
numérateurs:
8 fois 9 =72
3°)
Effectuer la multiplication des dénominateurs:
13
fois 11 = 143
5°)
Rendre compte sous forme d’égalité:
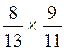 =
=![]()
Voici
trois cas :la multiplication ne pose pas de problème
particulier:
|
|
|
|
a)
Sans autre difficulté |
Corrigé : |
|
|
|
|
b ) idem |
Corrigé : |
|
|
|
|
c )idem |
Corrigé : |
|
|
|
TRAVAUX AUTO FORMATIFS.
1° ) A quoi est égal la multiplication de deux fractions de
dénominateur différent ?
2° ) Donner le modèle mathématique:
3° ) Donner la procédure permettant de calculer le produit de
deux fractions de dénominateurs différents.
1°) Faire les multiplications suivantes :
|
exercices |
corrigés |
|
a ) |
|
|
b) |
|
|
d ) |
|
|
c ) |
|
2 °)
idem
|
a ) |
|
|
b ) |
|
3°) Idem
|
a) |
|
|
b) |
|
4°) Faire les
multiplications suivantes :
|
|
|
|
a ) |
|
|
b ) |
|
|
c ) |
|
|
d ) |
|
|
e ) |
|