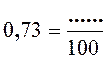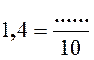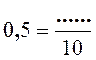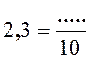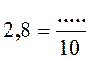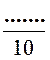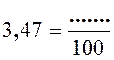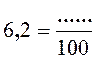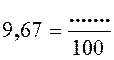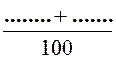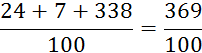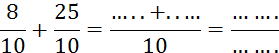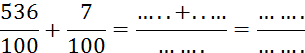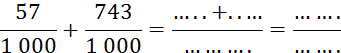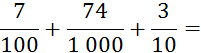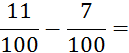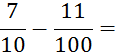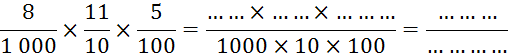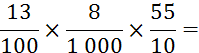|
Aller
vers lire….la numération
, ne pas confondre : « nombre » et
« grandeur » |
Pré requis:
|
|
|
|
Nomenclature |
|
|
Division de N par 10 ; 100 ;1000 |
ENVIRONNEMENT du dossier:
|
Objectif précédent : 2°)
Notion et idée du
nombre décimal . 4°) le nombre décimal et le système décimal. 5°)
Notion sur les opérations en primaire. 6°) Les nombres décimaux et le système métrique
( fiche travaux collège 6ème collège) . |
1°)
Numération des nombres décimaux. 2°) Classification des nombres décimaux 3°) Propriétés des opérations Net D. 4°) Les opérations dans « R »…… 5°) Cours- fiche de travaux collège complémentaire. 6°)
Suite : les 3 opérations avec des décimaux « addition , soustraction , multiplication et applications.
Collège 6ème . 7°) Suite :division avec des décimaux Collège 6ème
. |
COURS FICHE collège 6ème / 5ème |
|
Classe 6ème –cinquième-
collège :
Les « 3 » premières
Opérations avec des NOMBRES DECIMAUX
Et
avec des FRACTIONS DECIMALES.
Ne pas utiliser la calculatrice !!!!!!!!!!!!! faire les
activités et allez voir le corrigé .. !
|
Cette fiche traite à la fois des nombres décimaux
et leurs « parallèles » les fractions décimales. On n’oubliera pas de revoir
le cours sur la fraction décimale. |
|
||||||
|
|
|||||||
|
|
1°) Addition : |
|
|||||
|
|
|
|
|||||
|
|
2°) Soustraction . |
|
|||||
|
|
· Activités….. |
|
|||||
|
|
3°)
Fractions décimales : addition ,
soustraction. |
|
|||||
|
|
4°) Multiplication. |
|
|||||
|
|
5° ) Multiplication de
fractions décimales |
|
|||||
|
|
6°) CALCUL MENTAL . |
|
|||||
|
|
Ci-dessous des applications des
nombres décimaux. |
|
|||||
|
|
7 – OPERATEUR MULTIPLICATIF . |
|
|||||
|
|
|
|
|||||
|
|
APPLICATIONS INTERDISCIPLINAIRES. |
|
|||||
|
|
-
Périmètre. |
|
|||||
|
|
-
Situations problèmes
. |
|
|||||
|
|
|||||||
|
TEST |
COURS |
Interdisciplinarité Devoirs |
|
||||
|
|
|
|
|
>>> Liste de fiches de travaux avec les décimaux niveau 6
(primaire collège) autre
module « fiches » sue les décimaux |
|
||
COURS
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Complétez l’opération ci
contre. Comme on l’a déjà vu en primaire et en début de
formation. Quand on pose l’opération, il ne faut pas oublier d’écrire les
nombres de telle sorte que les virgules soient l’une sous l’autre. |
|
3 |
8 |
, |
4 |
7 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
+ |
|
1 |
, |
6 |
9 |
4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
….. |
……. |
…. |
….. |
…. |
… |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n° ….Calculez
mentalement. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3,74
+ 37 ,
4 = …………. |
0,7 + 0 , 3 = ……………… |
52,13
+ 18 ,
7 = ………………….. |
2,54 + 17 , 46 =
…………………. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0,009
+ 0,091 = ……………. |
149 + 0,05
= ……………………. |
0,54 + 0,
043 = …………… |
7,4 +
0,623 = ……………………. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« Ordre
de grandeur » un calcul d’ordre de grandeur permet d’éviter
des erreurs grossières. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Considérons la somme 39,236
+ 813 ,
47 · Un ordre de grandeur de
« 39,236 » est
« 40 » .
· Un ordre de grandeur de « 813 , 47 »
est « 810 » · Un ordre de grandeur de la somme est alors « 40 + 810 = ………… ?.. » Contrôler en faisant le calcul « 39,236 + 813 , 47 = ……… ? » Faite de même en complétant le tableau ci –
dessous : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Nombres à additionner. |
Calcul d’un nombre de grandeur .
|
Résultat exact. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
34,174 + 128 , 51 |
…………………..+ ……………………….= ………………….. |
……………… |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0,00682 +
0,0453 |
…………………..+ ……………………….= ………………….. |
……………… |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
65,64 + 8 , 127 |
…………………..+ ……………………….= ………………….. |
……………… |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« Propriétés » Les
propriétés de cette addition sont les mêmes que pour les entiers. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1°) Elle est commutative. 2°) Il existe un élément neutre qui est ….0……… 3°) Elle est associative. |
Précisez
oralement ce que cela signifie. ! |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n° ….Complétez le tableau
en calculant les sommes de chaque ligne et de chaque colonne ( essayer de faire le calcul mentalement ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
5,304 |
96 |
0,45 |
?............... |
En A = écrire la somme des termes de la dernière
ligne. …………….. En B = écrire la somme des termes de la dernière
colonne..
…….. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0,754 |
0,008 |
53,63 |
…………… ? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
21 |
9,16 |
1,765 |
?................... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
435,18 |
0,054 |
195,4 |
?..................... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
A =…………….. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
……………? |
…………..? |
…………? |
B =…………… |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
· Que pouvez vous dire des 2 résultats de : A
et B : ???????????????............................... · Dites en l’expliquant « oralement » si vous pouviez le
prévoir. ………………………………… |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 - Soustraction ( info + sur la soustraction avec les décimaux ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« a » et
« b » étant des décimaux quelconques ,
« a – b = x » signifie que
« a = b + x » |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Complétez l’opération ci
contre, comme vous l’avez appris en primaire. Faite la vérification : 18,63 +
35,907 : ……………………. |
|
5 |
4 |
, |
5 |
3 |
7 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
- |
1 |
8 |
, |
6 |
3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
…… |
……. |
… |
…. |
….. |
… |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°… : Calculez ( si possible) Vérifiez en faisant l’addition correspondante…………………. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Résultat |
|
Résultat |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
37, 66 - 16 ,
24 |
= ………………. |
Vérification : 16,24 + …………… |
= ………………. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7,6 – 0,0043 |
= ………………. |
|
= ………………. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0,024 - 0,00375 |
= ………………. |
|
= ………………. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0,067 – 0 , 132 |
= ………………. |
|
= ………………. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
83,51 - 1 ,
7 |
= ………………. |
|
= ………………. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°… : Pour chacun
des achats suivants, vous donnez 100€
, combien vous rend-on ? |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Pour 72 € on me rend………….. |
Pour 48,20
€ on me rend………….. |
Pour 9,75
€ on me rend………….. |
Pour 125,69 € on me rend………….. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°… : Complétez le tableau ci-dessous de telle sorte que l’on passe d’un nombre de la
première ligne au nombre correspondant de la deuxième ligne en ajoutant
« 7,52 » |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
5,7 |
0,085 |
12 |
|
|
25,3 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
« + 7,52 » |
|
|
|
|
|
|
« ? » |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
9,52 |
7,535 |
32,82 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
· Comment passe – t- on d’un nombre de la deuxième ligne au nombre
correspondant de la première ligne ? ………… …………….. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°… : On
choisit un nombre décimale , on lui ajoute
« 8,5 » , au résultat au retranche « 3,2 » au
nombre obtenu on retranche
« 4,1 » et enfin au nombre trouvé on ajoute
« 7,6 ». |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
+ 8,5 |
|
- 3,2 |
|
- 4,1 |
|
+7,6 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
…. |
|
27,6 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
……. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
· Faites de même dans le cas où le résultat final est « 37,27 » . Vous trouvez……………………….. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°… : Le
tableau ci-dessous donne les horaires des trains sur le trajet
« Marseille- Paris ». ( info + Sur le
système sexagésimal ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Départ « Marseille » |
Arrivée « Paris » |
Durée du trajet |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 h 37 min |
16 h 50 min |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
16 h 54 min |
23 h 37 min |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
21 h 52 min |
6 h 29 min |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3°)
Fractions décimales : addition ,
soustraction. ( voir cours1 précédent : les fractions décimales) ; voir autre la fraction
décimale : voir le cours 6ème ; |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Tout nombre décimal peut s’écrire sous la forme de fraction décimale . Exemples : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Nous allons calculer la somme de décimaux qui
sont écrits sous forme de fractions décimales . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n ° ….. Complétez 0,5 + 2 ,
3 = ……………. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Or vous savez que |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0,5 + 2 , 3
= ……2,8 …. S’écrit
alors : |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n ° ….. Complétez 3,47 +
6,2 = ……………. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Or vous savez que : |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3,47 +
6,2 = …9,67 s’écrit alors …. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Et vous remarquez que
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vous pouvez recommencer avec d’autres exemples,
vous constaterez que : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Règle : La somme de deux
fractions décimales de même dénominateur est une fraction décimale de même dénominateur, ayant pour numérateur
la somme des numérateurs. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Remarque 1 : reprenez le deuxième exemple et
comparez les additions. Vous retrouvez ainsi la règle de la position des virgules. |
|
3 |
4 |
7 |
|
|
3 , |
4 |
7 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
+ |
6 |
2 |
0 |
|
+ |
6, |
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
9 |
6 |
7 |
|
|
9 , |
6 |
7 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Remarque 2 : la règle s’applique aussi au cas de plus
de deux fractions :
On peut aussi proposer :
On vous demande de vérifier avec les nombres à
virgule : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n° : …Effectuez les calculs
suivants : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Cas où les fractions n’ont pas le même dénominateur. |
(info
plus …..addition de fractions de dénominateurs différents) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Exemple : ( On a réduit une fraction au même dénominateur que
l’autre ; pour obtenir le dénominateur commun (« 100 ») |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activités : Calculez de
même : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Info
++ : soustraction de deux fractions de même dénominateur. Info
++ : soustraction de deux fractions de dénominateur différent. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vous pouvez vérifier qu’on a la même règle que
précédemment en remplaçant le mot
« somme » par le mot « différence » (
lorsqu’elle existe) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Exemple : 0,8 - 0, 2
= ………………………… 0,8 – 0, 2 =
Activités : Calculez : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Ecriture d’un nombre décimal
sous forme de somme de fractions décimales. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Exemple : écrire 7,278 sous forme d’une somme de
fractions décimales |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
7,278 = 7
+ 0,2 + 0, 07 + 0, 008 |
= 7 + |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activités :
(idem que ci-dessus ) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
4,639 = |
0,395 = |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Complétez les opérations ci-dessous : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
8 , |
3 |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
4 |
5 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activités
n°…….Calculez 87 x 35 =
……………………………, ensuite sans faire d’autres calculs ,
complétez les opérations suivantes : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
8,7 x 0 ,35 = ……………………………….. |
350 x 0,87 = ………………….. |
8700 x 3500= …………………………… |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
35 000 x 87 = …………………………….. |
0,087 x 0,035 = …………………………. |
0,0087 x 0,0037 = …………………………. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0,000 87 x
35 = ………………………………. |
3,5 x 870
= ………………………………….. |
0,00035 x
84 000 = ………………………… |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Comme pour l’addition, pour éviter des erreurs
grossières, il est recommandé de faire un calcul d’ordre de grandeur avant d’effectuer une
multiplication. |
||||||||||||||||||||||||||||||||||||
|
|
C’est ce que nous allons faire pour le produit
« 48,675 x 823,19 » . Un ordre de grandeur de «
48,675 » est « 50 » . et un ordre de grandeur de « 823,19 » est « 800» . Un ordre de grandeur du produit est alors de
« 50 x 800 = ……………… »
Contrôle :
en faisant le calcul « 48,675 x 823,19 = …………………………………. » . |
||||||||||||||||||||||||||||||||||||
|
|
Activités n° …………… |
||||||||||||||||||||||||||||||||||||
|
|
Nombres à multiplier |
Calcul d’un ordre de
grandeur |
Résultat exact. |
||||||||||||||||||||||||||||||||||
|
62,534 x 0 ,
008 61 |
……………………x…………………..=………………… |
………………………………….. |
|||||||||||||||||||||||||||||||||||
|
0,0275 x 0 , 000 428 |
……………………x…………………..=………………. |
………………………………….. |
|||||||||||||||||||||||||||||||||||
|
0,371 x 73 683,52 |
……………………x…………………..=…………………. |
………………………………….. |
|||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
Les propriétés de cette multiplication sont les
même que pour les entiers. |
||||||||||||||||||||||||||||||||||||
|
|
1°) Elle est « commutative ». 2°) Il existe un « élément neutre » qui
est « 1 ». 3°) Elle est « associative ». 4°) Pour tout décimal « x » : x |
Précisez ce que cela signifie (
en utilisant un exemple ….) |
|||||||||||||||||||||||||||||||||||
|
|
Autres propriétés : |
||||||||||||||||||||||||||||||||||||
|
|
Vous savez que « 2 , 6 >
1 » et que « 0,7
< 1 » |
Calculer : « 5,3 |
|||||||||||||||||||||||||||||||||||
|
|
« 5,3
|
Trouvez-vous un nombre plus grand ou plus petit
que « 5,3 » ?.............................................. |
|||||||||||||||||||||||||||||||||||
|
|
« 5,3
|
Trouvez-vous un nombre plus grand ou plus petit
que « 5,3 » ?.............................................. |
|||||||||||||||||||||||||||||||||||
|
|
Faîtes d’autres essais, vous constaterez
que : |
||||||||||||||||||||||||||||||||||||
|
|
Quand on multiplie un nombre « a » ·
Par un nombre plus
grand que « 1 », on obtient un nombre plus …… ………….que « a » ·
Par un nombre plus
petit que « 1 », on obtient un nombre plus …… ………….que « a » |
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
Activités :…n°…. |
||||||||||||||||||||||||||||||||||||
|
|
Une personne achète du vin à 6,50 € Elle en remplit une bonbonne de 12,8 L et des
bouteilles de 72 cL. 1°) Quel est le prix du vin contenu dans la
bonbonne ? 2°) Quel est le prix du vin contenu dans chaque
bouteille ? |
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
MULTIPLICATION DE FRACTIONS DECIMALES. |
Info 1 + : la multiplication de deux fractions de dénominateurs
différents. Info 2 + : la
multiplication de deux fractions de même dénominateur. |
|||||||||||||||||||||||||||||||||||
|
|
Nous allons calculer le produit de décimaux
écrits sous forme de fractions décimales. |
||||||||||||||||||||||||||||||||||||
|
|
Exemple 1 : Complétez le calcul : 0,3 Or vous savez que
0,3 = Aussi :
0,3 Vous remarquerez que : ( |
||||||||||||||||||||||||||||||||||||
|
|
Exemple 2 : Complétez le calcul : 1,2 Comme vous l’avez vu précédemment : 1,2 Et vous remarquerez que Vous pouvez recommencer avec d’autres exemples,
vous constaterez toujours que : |
||||||||||||||||||||||||||||||||||||
|
|
Le
produit de 2 fractions décimales est une (troisième) fraction décimale dont le numérateur est le
produit des numérateurs et le dénominateur le produit des dénominateurs. |
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
Remarque 1 : |
||||||||||||||||||||||||||||||||||||
|
|
Si vous reprenez le deuxième exemple et comparez
les multiplications ,vous retrouvez ainsi la règle
de la virgule. |
|
|
|
1, |
2 |
|
||||||||||||||||||||||||||||||
|
0, |
0 |
4 |
|||||||||||||||||||||||||||||||||||
|
0, 0 |
4 |
8 |
|||||||||||||||||||||||||||||||||||
|
|
Remarque 2 : |
||||||||||||||||||||||||||||||||||||
|
|
La règle s’applique aussi au cas de plus de deux
fractions ;
|
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
Activités n° …. : Calculez : |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
6 - CALCUL
MENTAL. |
||||||||||||||||||||||||||||||||||||
|
|
a)
« multiplication
par « 0,5 » |
||||||||||||||||||||||||||||||||||||
|
|
Vous savez que 0,5 = |
||||||||||||||||||||||||||||||||||||
|
|
Règle : multiplier par « 0,5 » revient à diviser ce nombre
par « 2 » |
||||||||||||||||||||||||||||||||||||
|
|
14 |
27 |
|||||||||||||||||||||||||||||||||||
|
|
Calculez mentalement : |
||||||||||||||||||||||||||||||||||||
|
|
8 |
96 |
142 |
45 |
|||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
b)
« multiplication
par 0,1 ; 0,01 ; 0,
001 ; etc. » |
||||||||||||||||||||||||||||||||||||
|
|
Vous savez que 0,1 = De même 0,01 = |
||||||||||||||||||||||||||||||||||||
|
|
· Multiplier un nombre par « 0,1 » revient à diviser ce nombre par
………. « 10 » · Multiplier un nombre par « 0,01 » revient à diviser ce nombre par
………. « 100 » · Multiplier un nombre par « 0,001 » revient à diviser ce nombre par
………. « 1 000 » |
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
Activités : N°……….. |
||||||||||||||||||||||||||||||||||||
|
|
18 |
49 |
34 |
||||||||||||||||||||||||||||||||||
|
4,7 |
0,01 |
0,001 |
|||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
Ci-dessous des applications des
nombres décimaux. |
||||||||||||||||||||||||||||||||||||
|
|
7 – OPERATEUR MULTIPLICATIF. |
|
|||||||||||||||||||||||||||||||||||
|
|
L’opérateur multiplicatif est un nombre qui peut
être « entier » , « décimal » ou
« fractionnaire » On vous demande de traiter les trois cas. |
1°)Fiches en lien avec des tableaux
« proportionnels » 2°) les
proportionnalités.(sommaire) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
Activité n°1 : · On vous demande de remplir le
tableau ci-dessous. |
|
|||||||||||||||||||||||||||||||||||
|
|
· Trouvez la valeur de
l’opérateur multiplicatif permettant de passer d’une ligne du tableau
à l’autre. · Faire la représentation graphique (comme vu à la leçon sur
la gestion des données et statistique…) |
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
5 |
10 |
0,5 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
10 |
|
|
15 |
6 |
2 |
|
||||||||||||||||||||||||||||||
|
|
Ici , posez le calcul qui permet de déterminer la
valeur numérique de l’opérateur multiplicatif : Commentaire concernant la représentation graphique : A chaque colonne du tableau (lecture verticale)
correspond un couple de nombres. A la première colonne correspond le couple ( 5 ; 10 ) . ( « 5 » est appelé « abscisse ») ;
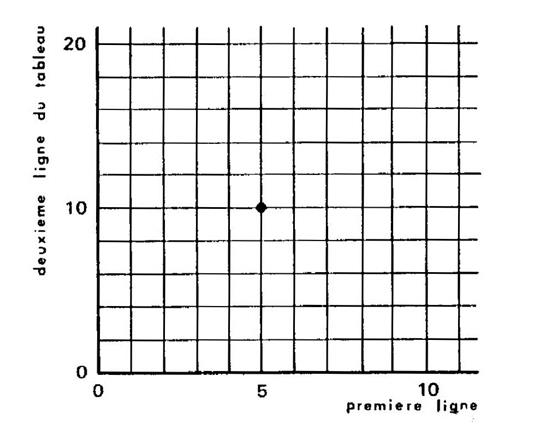
« 10 » est appelé « ordonné ») Dans le repère ci-contre le point de coordonnés ( 5 ; 10 ) a déjà été placé. A vous de placer les autres points. |
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
Activité n°2 : On vous demande de remplir le tableau ci-dessous. |
|
|||||||||||||||||||||||||||||||||||
|
· Trouvez la valeur de
l’opérateur multiplicatif permettant de passer d’une ligne du tableau
à l’autre. · Faire la représentation graphique (comme vu à la leçon sur
la gestion des données et statistique…) |
|
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
21 |
15 |
3 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
7 |
|
|
4 |
6,5 |
2 |
|
||||||||||||||||||||||||||||||
|
|
On passe de la première ligne du tableau à la
deuxième ligne du tableau en divisant par « 3 ». Or vous savez que multiplier par On pourra donc comme opérateur « |
||||||||||||||||||||||||||||||||||||
|
|
Commentaire concernant la représentation graphique : On vous demande de choisir convenablement l’unité
sur chaque droite graduée (appelée :
horizontalement : « axe des abscisses » ,
et verticalement appelée « axe des ordonnées ) . Ce choix sera déterminé pour placer tous les
nombres du tableau et de telle sorte que le dessin soit le plus grand
possible. Ceci fait, placer les points comme dans
l’activité « 1 ». Vous constatez aussi que tous les points que vous
avez placez sont « ……………….. » (prendre une règle) |
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
Activité n°3: On vous demande de remplir le tableau ci-dessous. |
|
|||||||||||||||||||||||||||||||||||
|
· Trouvez la valeur de
l’opérateur multiplicatif permettant de passer d’une ligne du tableau
à l’autre. · Faire la représentation graphique (comme vu à la leçon sur
la gestion des données et statistique…) |
|
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
7 |
14 |
17,5 |
|
3,5 |
21 |
|
|
||||||||||||||||||||||||||||
|
|
3 |
6 |
7,5 |
4,2 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
L’opérateur multiplicatif ( si
il existe) qui permet de passer de la première
ligne à la seconde ligne , est le nombre par lequel il faut multiplier
« 7 » pour obtenir « 3 » . C’est le quotient de « 3 » par
« 7 » qui s’écrit « (voir le cours sur …….) Vérifiez que cet opérateur convient bien pour les
autres nombres du tableau et complétez celui –ci. Faites la représentation graphique comme dans les
activités précédents. Vous constatez aussi que les points sont
…………… « ……………………». |
|
|||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||
|
|
APPLICATIONS INTERDISCIPLINAIRES. |
|
|||||||||||||
|
|
|
Info
arithmétique : fiche de travaux sur le calcul des périmètres. |
|
||||||||||||
|
|
|
|
|||||||||||||
|
|
Le calcul de périmètre. (info
++ sur le calcul des périmètres) |
|
|||||||||||||
|
|
|
||||||||||||||
|
|
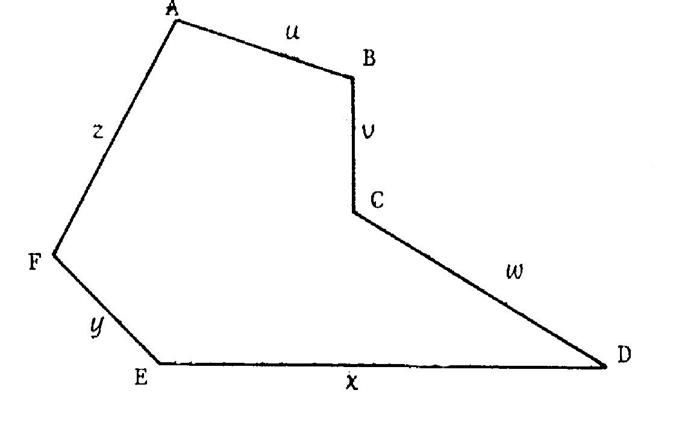
Voici un polygone « ABCDEF ». Appelons « u », « v »,
« w », « x » ,
« y » , « z » , les mesures faites avec la même
unité des longueurs des côtés du polygone. (vois ci -contre). La mesure
(avec La même unité) du périmètre du polygone « ABCEDEF »
est alors :
« u + v + w + x + y + z ». Activité n°1 : Mesurez au « mm » prés
la longueur de chacun des côtés du polygone et détermine ainsi une valeur
approchée en « mm » de la mesure du périmètre du polygone
« ABCDEF » : …………+…………+……….+………..+ ………+ ………..= ………………………… |
|
|
||||||||||||
|
|
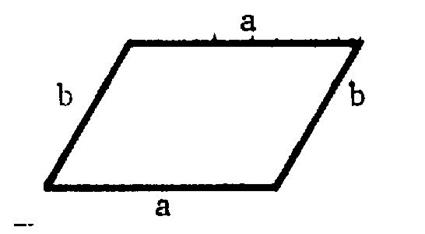
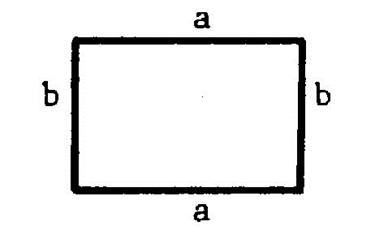
Périmètre du parallélogramme et du rectangle : |
|
|||||||||||||
|
|
Vous savez que dans tout parallélogramme les
côtés opposés ont la même : …………..………… (info plus…) |
|
|
||||||||||||
|
Il en est de même pour tout rectangle car tout
rectangle est un « ……………………………. » |
|
||||||||||||||
|
|
Appelons « a » et « b » les
mesures des longueurs des côtés ( voir les figures
ci-dessus) Et désignons par « P » la mesure du
périmètre. ( les mesures sont ,bien entendu , exprimées
dans la même unités) (tout en
« mm » ; ou tout « cm » ,
…) On a alors : « P =
a + b + a + b » ou
encore : « P = ( a + b) + ( a + b
) » Ce qui peut s’écrire : « P = 2 fois ( a +
b) » qui s’écrit : « P = 2 Remarque : ( a + b) est appelé « le demi
–périmètre » . |
|
|||||||||||||
|
|
Activités n° 2 : Chaque
colonne du tableau ci-dessous correspond à un rectangle ( lorsqu’il
existe). On vous demande de compléter ce tableau ( si
possible) , attention ! :
vous devez penser à transformer les unités ,il faut
les homogénéiser (même unité) |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Longueur |
43 mm |
11,2 m |
10,5 cm |
|
||||||||||
|
Largeur |
0,025 m |
4 cm |
3,2 m |
||||||||||||
|
Périmètre |
428 mm |
38 m |
5 300 mm |
0,42 m |
|||||||||||
|
|
|
|
|||||||||||||
|
|
|
||||||||||||||
|
|
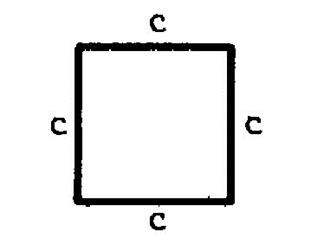
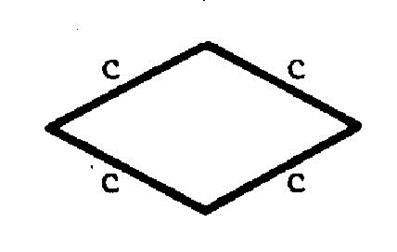
Vous savez que tous les carrés ou tous les losanges ont les quatre côtés
de même « ………………………. ». |
|
|||||||||||||
|
|
|
|
|
||||||||||||
|
|
Nous appelons « c » la mesure de la
longueur de chaque côté de la figure
et « P » la mesure du périmètre ( dans
la même unité de mesure). On a alors : « P = c + c + c + c » et l’on écrit que « P = 4 |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Activité n°3 : Dans le tableau ci-dessous ,
les nombres de la première ligne sont les mesures en « cm » des
côtés de certains carrés (une colonne = un carré). Les nombres de la deuxième
ligne sont les mesures en « cm » des périmètres des carrés
correspondants. Complétez ce tableau. Vous pouvez être amené à faire certaines
remarques, faites en part à votre
professeur. |
|
|||||||||||||
|
|
Côté |
0,1 |
0,2 |
|
|
|
1 |
2 |
5 |
10 |
|
||||
|
Périmètre |
|
|
4,8 |
12 |
24 |
|
|
|
|
||||||
|
|
|
|
|||||||||||||
|
|
Activité n°4 : |
|
|||||||||||||
|
|
Dans tout « triangle
isocèle » , on appelle « base » ,
le côté qui n’a pas la même longueur que les deux autres. |
|
|
||||||||||||
|
|
On vous dit que le périmètre d’un triangle
isocèle est de « 23,55 cm ». La base a pour longueur
« 3,55cm » . On vous demande de calculer la longueur de chacun
des deux autres côtés de ca triangle. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
SITUATIONS PROBLEMES LS.P.) |
|
|||||||||||||
|
|
S.P. n°1 : La longueur d’un rectangle est de 21 cm. Sa
largeur est les Quel est le périmètre de ce rectangle ? |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
S.P. 2 |
|
|||||||||||||
|
|
Une balle élastique rebondit aux Sachant que la balle est lâchée d’une hauteur de
6 m . Quelle est la hauteur du premier rebond ? Quelle est
la hauteur du second rebond ? Quelle est la hauteur du troisième rebond ? |
|
|||||||||||||
|
|
|
||||||||||||||
|
|
S.P.3 : »Budget tabac » |
|
|||||||||||||
|
|
Dans une famille de fumeurs: Le père fume chaque jour en moyenne 20
cigarettes, ce qui correspond à un paquet coûtant « 7,60 € » .
Il fume également la pipe, en moyenne, il achète chaque semaine un paquet de
tabac coûtant « 9,70 € » .IL
fume aussi le cigare, la dépense correspondante est en moyenne de
« 67,50 € » par mois. La mère fume en moyenne 10 cigarettes par jour.
Elle achète tous les deux jours un paquet coûtant « 9,80 € ». Questions : |
|
|||||||||||||
|
|
1°) Combien ce ménage dépense-t-il annuellement pour
sa consommation de tabac ? |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
2°) Sachant qu’un ………………… coûte « 42 € », combien peut-on
acheter de …………….avec la somme dépensée « en fumée » ?. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
S.P. N°4 |
|
|||||||||||||
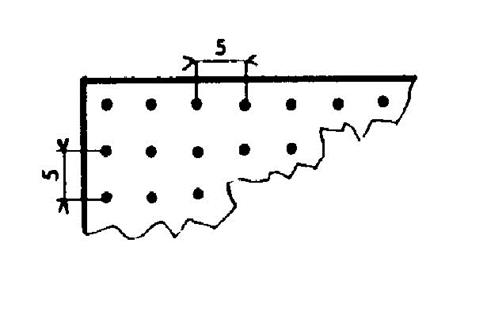
|
|
Un champ a la forme d’un carré de 75 m de côté. A « 2,5m » du bord de ce champ ( à l’intérieur), on plante une rangée d’arbres. Ces arbres sont alors situés sur le pourtour d’un
carré. Il y a un arbre à chaque sommet. Quel est le nombre d’arbres ? |
|
|
||||||||||||
|
S.P. n°5 |
|
||||||||||||||
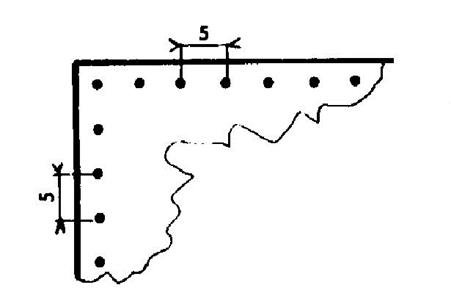
|
Dans un champ rectangulaire dont les longueurs
des côtés sont « 95 m » et « 40 m », on veut planter des
arbres d’une même rangée sont distants de s
« 5 m » et ils sont
situés à « 2, 5 m »du bord. Combien d’arbres peut-on planter ? |
|
||||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
TRAVAUX AUTO
FORMATIFS (devoir formatif)
CONTROLE :
Revoir les
textes dans les « encadrés »
EVALUATION
Refaire
les activités ……………….