Pré requis:

Collège : niveau 6 -5^ème
Le repérage.
Le papier millimétré
Lieu géométrique : INFO
Repérage d’un point dans un repère cartésien orthonormé

ENVIRONNEMENT du dossier:

			Les Statistiques info : liste des cours
Index : warmaths	Objectif précédent 1°) Les graphiques vus en primaire (inventaire) 2°)Toutes les représentations graphiques de base en statistique.	Objectif suivant : 1°) Exploitation graphique. 2°) Les « fonctions » et les: principales représentations graphiques 3°) Statistique (gestion de données) : les principaux graphiques..	/ 5 Les représentations graphiques et les fonctions Liste des cours de 6^ème collège

DOSSIER :

Statistiques : Gestion de données ( Approches)

					>>>>CORRIGE du cours.
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

	La représentation graphique dans la gestion de données .
	Autre type de représentation : L’ HISTOGRAMME.
	Recherche de « pourcentage »
	Application : L’ Etude d’une situation problème en statistique concernant  : « Une classe d’élèves …….. »
	(pourcentage ; taille ; poids ; représentations graphiques (histogramme ; diagramme en bâtons)
Info. COURS

Pré @requis.		La représentation graphique dans la gestion de données .
		Exemple 1 :
		Le tableau ci-dessous donne les importations de la France en pétrole brut ( en millions de tonnes) de l’année « 1967 » à l’année « 1978 »
		Année					67						68					69						70			71					72		73						74		75				76				77		78
		Importation -pétrole					72						82					90						100			110					121		135						130		106				121				117		116
		Remarque : et à chaque colonne du tableau correspond un couple de nombres ( exemple : à la 5^ème colonne du tableau correspond le couple de nombre ( 71 ; 110 ). Travail demandé : On vous demande de faire une représentation graphique de ces données ; c'est-à-dire : Représenter la quantité de pétrole brut importé « en fonction » des années. Pour ce faire : suivez les explications données ci-dessous ,en respectant cette procédure !!! On sait qu’à chaque « colonne » est limité à un couple de nombres . ( soit deux nombres)
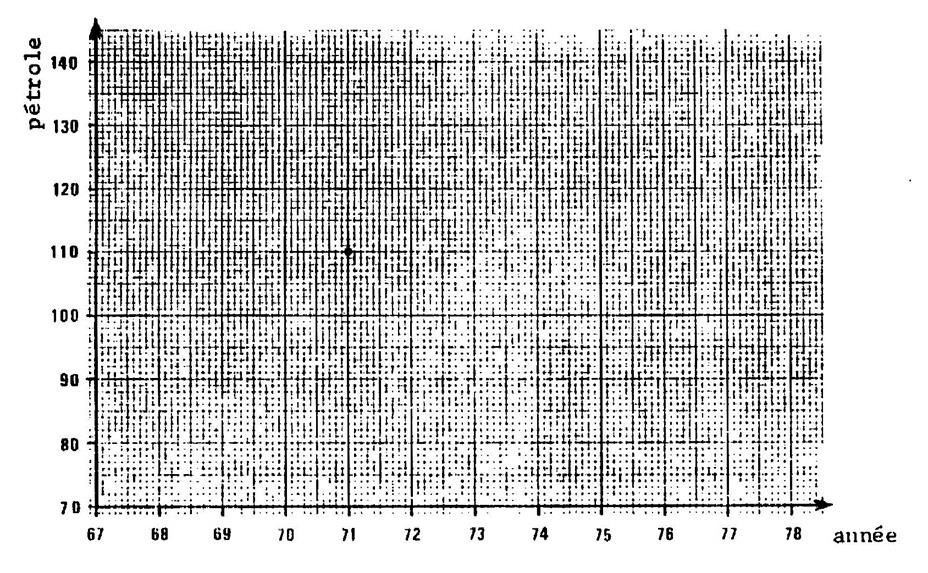
		Voir le repère fourni (voir ci contre) A chaque couple , on associe un point sur le dessin ; de la façon suivante : Par exemple (voir ci contre), on a déjà placé le point correspondant à ( 71 ; 110 ) · « 71 » ( qui est le premier terme (nombre) du couple)se lit sur la droite marquée « année ». · « 110 » ( qui est le deuxième r terme (nombre) du couple)se lit sur la droite marquée « pétrole ». Sur ces deux droites figure une graduation régulière ( avec des unités différentes)
		Reproduire sur une copie blanche le repère ci contre et ; Placer de même tous les points. · pour les années ; prendre 1 cm pour 1 an . · Pour le pétrole : prendre 1 cm pour 10 millions de tonnes.
		Pour avoir une vision globale de «l’  allure ( qui monte ou qui descend)  »de ces points , on peut joindre ces points successifs , cela revient à tracer des segments ( en bleu) Attention : ces traits ( dans ce cas ) n’ont pas de signification . Ils permettent seulement de mieux voir l’évolution des approvisionnements .
		Etude du tracé :
		1°) Que constate – t- on ? On constate que : - de 1967 à 1973 : les importations de pétrole ont augmenté. - Que de 1973 à 1975 : les importations ont diminuées…. (Pour en savoir plus sur la raison de cette diminution , allez voir sur Internet : « choc pétrolier 1974 » )
		2°) En quelle année la quantité de pétrole a – t- elle été la plus petite ?
		3°) En quelle année la quantité de pétrole a – t- elle été la plus grande?
		Exemple 2 :
	Heure					0		1					2					3						4			5					6		7						8		9				10				11		12
	Température					3		2					4					4						4			6					8		8						9		10				10				11		13
	Heure					12h30		13					14					15						16			17					18		19						20		21				22				23		24
	Température					14		15					17					16						16			15					15		14						13		10				10				7		4
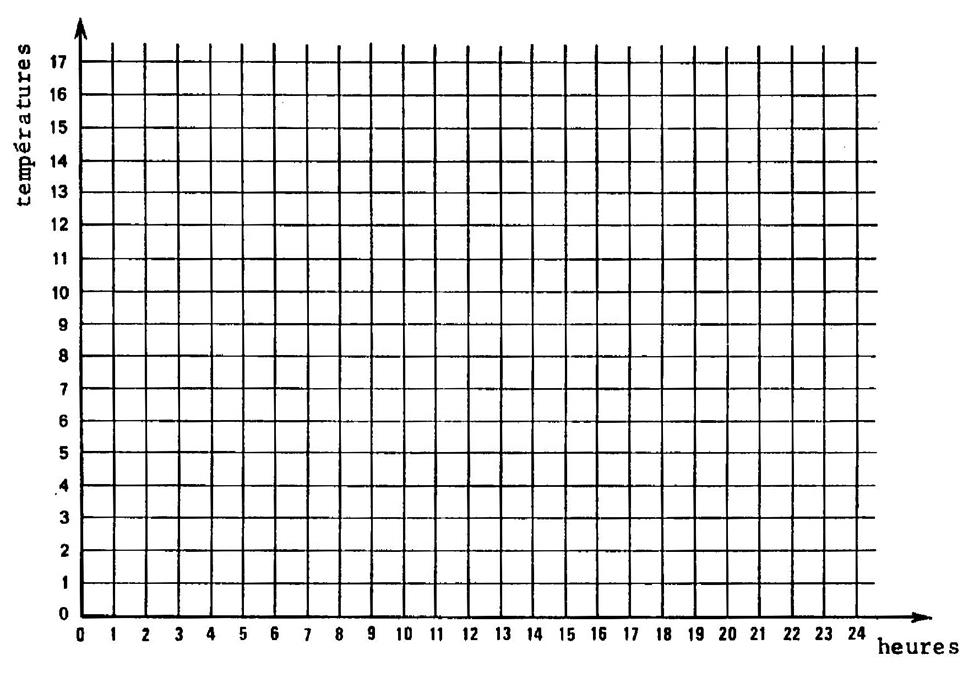
Travail demandé : Faire la représentation graphique correspondante.
	La température évoluant ( elle varie constamment ( en + ou en - ) dans le temps) , vous pouvez joindre les points successifs pour former une ligne régulière continue. ( contrairement au premier exemple , dans lequel on évite de tracer des segments de droite) Cette ligne régulière continue ( que l’on appelle « courbe ») à cette fois –ci une signification. On imaginera  : qu’elle est constituée par une infinité de points qui représentent chacun à la fois un instant déterminé et la température correspondante.
	Remarques : - Il existe un appareil appelé « thermomètre enregistreur » qui trace sur une feuille ( enroulé sur un cylindre ) une courbe comparable à celle que vous venez de tracer. - Il existe aussi un baromètre enregistreur qui trace sur une feuille la variation de la pression atmosphérique en fonction d’une durée déterminée , d’autres diront aussi : « en fonction temps qui s’écoule » …
	Exercices :
	A l’aide de la courbe que vous avez tracé , déterminez « approximativement » ( en minimisant l’erreur )
	1°) la température qu’il faisait à 1 h 30 mn : ……………( 3°).
	2°) Les moments de la journée où la température était de 13° :………………………………………….( 12 h et 20 h )
	3°) Vers quelle heure la température était minimum. ? …………………… Quel était ce minimum ?.............
	3°) Vers quelle heure la température était maximale . ? …………………… Quel était ce maximum ?.............
	4°) De quelle heure à quelle heure la température à augmenté ?....................................
	5°) De quelle heure à quelle heure la température à diminué ?....................................
	Autre type de représentation : L’ HISTOGRAMME.
	Activité « élève » : Vous allez choisir un texte quelconque ( différent de celui de vos camarades ). On vous demande de compter combien de fois apparaissent les voyelles ( « a » , « e » « i » , « o » ,  « u » et la demi voyelle « y ») dans une partie de texte . Vous arrêtez quand vous aurez compté « 100 » voyelles et demi -voyelles. Vous procéderez de la manière suivante : Imaginons que vous rencontrez successivement les voyelles : a ; e ; e ; i ; a ; u ; y ; ……..
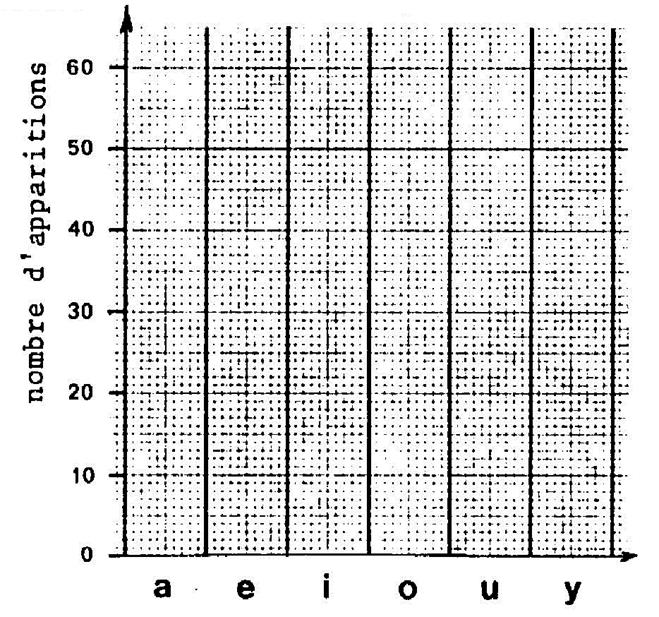
	Vous remplissez alors le diagramme ci-dessous comme il est indiqué ci-contre,  : Pour chaque voyelle tracez un petit trait de ( 1 mm de haut ) dans la colonne correspondant à la voyelle.
	Ceci terminé , vous obtenez , dans chaque colonne , un rectangle dont la hauteur vous donne le nombre d’apparitions de la voyelle considérée. Un tel diagramme s’appelle un « histogramme » Ceci fait : lisez sur votre diagramme le nombre trouvé pour chaque voyelle , vérifiez que le total fait bien « 100 » et complétez le tableau ci -dessous;
	Lettre									a												e									i							o							u						y
	Nombre
	Recherche de « pourcentage »
	· Supposons que vous ayez trouvé « 17 » lettres « a » : On peut dire alors qu’il y a «  17  a » pour « 100 » voyelles. On dit encore : Parmi les voyelles , il y a 17 pour 100 « a ».
	17 pour 100													S’écrit					17 %									Et s’appelle							pourcentage
	On vous demande de donner les pourcentages que vous avez trouvées pour chacune des voyelles
	17 % de « a »					……….% de « e »											……….% de « i »												……….% de « o »										……….% de « u »								……….% de « y »
	Activité « groupe » : Vous allez regrouper les résultats trouvés par l’ensemble des élèves de la classe ;
	Après avoir totalisé les résultats trouvés par tous les élèves , on vous demande de compléter le tableau ci-dessous :
	Lettre								« a »											« e »									« i »							« o »							« u »					« y »
	Nombre total
	Moyenne
	Pourcentage
	· On vous demande de ranger les voyelles de la plus fréquente à la moins fréquente………………………………………………………………………………
	· A partir des résultats trouvés ci-dessus , dans un texte comportant « 1 000 » voyelles , combien peut-on s’attendre à rencontrer de :
				« a » ? ………					« e » ? ………											«  i » ? ………									«  o » ? ………							«  u » ? ………							«  y » ? ………
	Et dans un texte contenant 350 voyelles
	Exemple d’une SITUATION PROBLEME . Dans le tableau ci-dessous on y trouve les renseignements concernant les élèves d’une classe.
			NOM Prénom														Sexe									Date de naissance							Taille en cm.								Poids en kg
	1.		BARDON Claire														F									21- 8 - 99							144								35
	2.		BORRELLI Victor														M									11 – 1 - 98							152								40
	3.		CARNOI Patricia														F									28 - 12 - 99							145								32
	4.		CAUDRE Gilbert														G									5 – 9 - 99							136								33
	5.		CHARLOT Nicolas														G									23 – 10 – 00							126								27
	6.		DESCART Violaine														F									30-4 - 98							141								36
	7.		ERBERT Jacques														G									6 – 7 – 97							157								43
	8.		EULER Fred														G									18 – 9 - 99							143								35
	9.		FROMENT Paul														G									31 – 3 - 99							147								33
	10.		GADROIT Delphine														F									10 – 10 - 98							149								42
	11.		GAUSS Dominique														F									22 – 7 - 99							148								40
	12.		HUBERT Sandrine														F									20 – 3 - 98							138								31
	13.		LANGOGNE Pierre														G									17 – 6 - 99							142								36
	14.		LAPOULE Suzanne														F									22 – 6 - 98							152								43
	15.		LEMPEREUR Lucile														F									10 – 8 - 99							142								39
	16.		MACAIGNE Charline														F									5 – 5 - 99							134								34
	17.		MONTRE Ange														F									15- 3 - 80							148								33
	18.		PATE Raymond														F									25 – 11 - 99							144								37
	19.		PENTRE Véronique														F									3 - 6 - 97							154								46
	20.		POINE Victoria														F									11 – 11 - 99							139								40
	21.		PORTRIR Gisèle														F									17 – 3 - 98							145								33
	22.		RATBURD David														G									27 – 2 - 98							142								35
	23.		TALON Maryse														F									18 – 4 - 99							140								37
	24.		THILOUR Luc														G									11 – 7 - 00							131								31
	25.		ZORRA alexandre														G									27 – 4 - 00							136								29
	ACTIVITES POSSIBLES :
info@	1°) Pourcentage de filles et de garçons dans cette classe. Dans cette classe de 25 élèves , combien y a - - t- il de garçons ? ……………………………. ;et de filles ?.................................. En imaginant une classe de 100 élèves , composée de la même façon, c'est-à-dire avec la même proportion de filles et de garçons , il y aurait ……….fois plus d’élèves , donc ………fois plus de filles ( et de garçons ) c'est-à-dire …………….filles et …………….garçons. On peut donc dire : il y a …………….% de filles et ……………..de garçons.
	2°) Répartition des années de naissante.
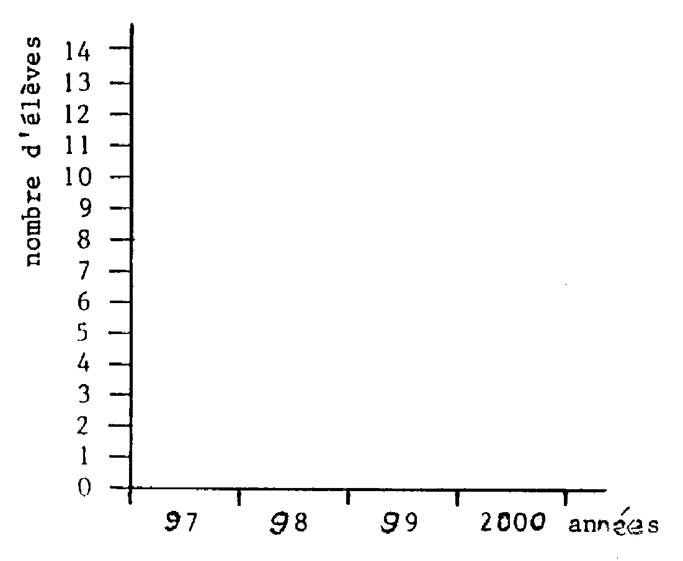
	Compte combien d’ ‘ élèves sont nés la même année et complétez le tableau .
	Année					97			98								99								00
	Nombre d’élèves
	Faire l’ histogramme correspondant.
info@	3°) Tailles des élèves :
	On vous demande dans ce chapitre de calculer la « taille moyenne » dit aussi « combien ils mesurent en moyenne » , des élèves de la classe , c'est-à-dire : faire la moyenne des tailles. ( intérêt de ce calcul ? )
	Pour faire ce calcul de la moyenne , il faut faire la somme de toutes les tailles et puis diviser par le nombre d’élèves.
	Remarque : la liste des tailles des élèves n’est pas une information très parlante . ( pour vous amusez vous reportez dans un repère des points dont le couple de nombre est ( numéro de l’élève et sa taille) : exemple point 1 ( 1 ; 144 ) ; ensuite ( 2 ; 153 ) ; ( 3 ; 145) ; ( ………
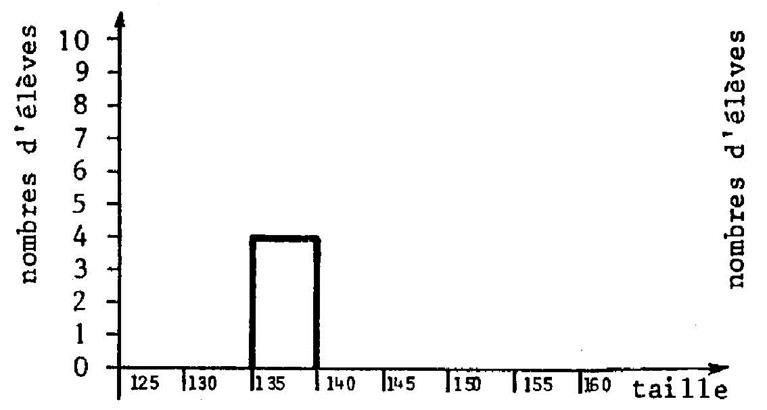
	On vous propose , que, pour mieux étudier la répartition des différentes tailles , de faire ce que l’on appelle « un histogramme » , comme cela a été fait pour les années de naissance. Procédure : · Pour simplifier l’étude nous choisissons de regrouper les tailles de 5 cm en 5 cm ( non de 1cm par 1 cm ). · Construire et compléter le tableau ci-dessous :
	Taille en cm.				De 125 inclus à 130 exclu.						De 130 inclus à 135 exclu.										De 135 inclus à 140 exclu.									De140 inclus à 145 exclu.							De 145 inclus à 150 exclu.							De 150 inclus à 155 exclu.					De 155 inclus à 160 exclu.
	Nombre d’élèves
	Calculez le pourcentage de chaque tranche de tailles (compléter le tableau ci-dessous)
	Pourcentage
	Ensuite : Faire l’histogramme correspondant . ( complétez le graphique ci-contre)
	Autre moyen de représentation graphique :
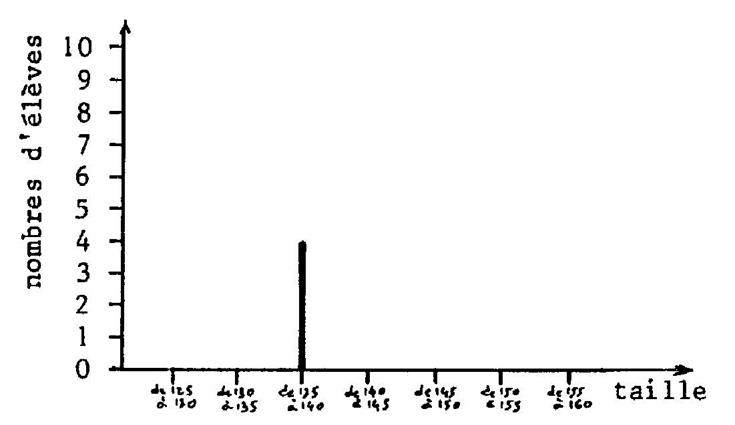
	Au lieu de dessiner des rectangles comme dans le graphique ci-dessus ( histogramme) on décide de tracer des segments de droites , dans ce cas le graphite portera le nom de « diagramme en bâtons »
	4°) « Poids » des élèves
	(@ ne pas confondre « poids » et « masse » L’usage veut que l’on dise « poids » alors que l’on devrait dire « masse »
	a) on vous demande de calculer le poids moyen des élèves de la classe. ( vous trouvez : ………………………..) b) On vous demande de compléter le tableau ci-dessous. ( on vous impose : les poids sont rangés de 3 kg en 3 kg)
	Poids en kg.				De 26 inclus à 29 exclu						De 29 inclus à 32 exclu										De 32 inclus à 35 exclu									De35 inclus à 38 exclu							De 38 inclus à 41 exclu							De 41 inclus à 44 exclu					De 44 inclus à 47 exclu
	Nombre d’élèves.
	Pourcentage %
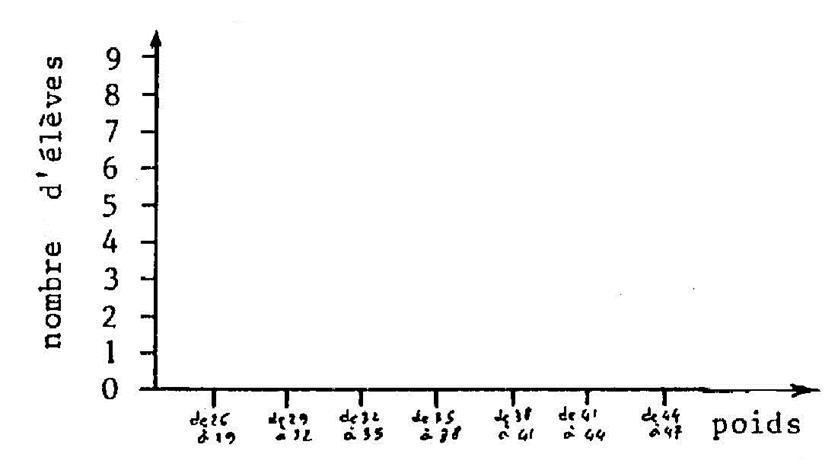
	On vous demande de faire les représentations graphiques
	Faire l’histogramme correspondant :
	Faire le diagramme en bâtons correspondant

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1°) Citer les différentes possibilités de représenter graphiquement une série statistique vu dans le cours.

EVALUATION :

Refaire les travaux du cours……………

(pour le corrigé voir le cours)