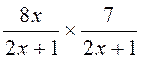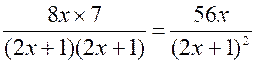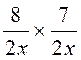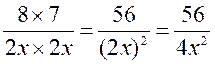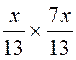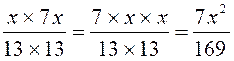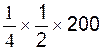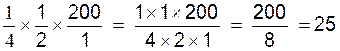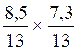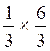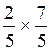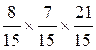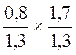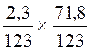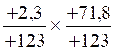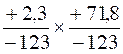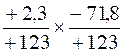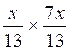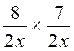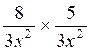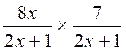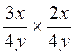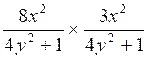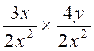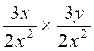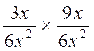|
|
Expression
d' un résultat
|
|
|
|
|
|
|
ENVIRONNEMENT du
dossier :
|
|
Liste des
cours sur le multiplication et les fractions…. |
DOSSIER: MULTIPLICATION de deux fractions de même
dénominateur .
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Devoir Contrôle |
Interdisciplinarité |
|
Remarque
importante: Il n’y a pas de difficulté particulière pour effectuer la
multiplication de deux fraction.
Nous pouvons
multiplier ,directement, deux fractions qui ont
le même dénominateur ou deux fractions qui n’’ont pas le même dénominateur.
CAS GENERAL : Multiplication de deux fractions
(ou écriture(s) fractionnaire(s) .
La
multiplication de deux fractions est égale à une troisième fraction qui aura
pour: Numérateur le produit des numérateurs et pour Dénominateur le produit des
dénominateurs.
A SAVOIR: Forme littérale:
Règle :
La multiplication de deux
fractions de même dénominateur est égale
à une troisième fraction qui aura pour: « Numérateur » le produit des
numérateurs et pour « Dénominateur » le produit des dénominateurs.
Forme
mathématique :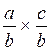 
= 
=
Exemple :
Faire le calcul suivant :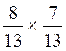 
Procédure
pour multiplier deux fractions de même dénominateur:
On suivra la procédure suivante
1° )construire une égalité (voir objectif:
EG 1) dont le premier membre est
l’énoncé (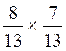) et le deuxième
membre est la fraction dont le numérateur sera le produit des numérateurs des
fractions du premier membre et le dénominateur le produit des dénominateurs
communs (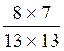
)
soit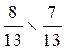 
= = 
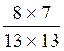3°) Effectuer la multiplication des
numérateurs:
8
fois 7 =56
4°)
Effectuer le produit des dénominateurs:
13 fois 13 = 143 = 13 2
5°)
Rendre compte sous forme d’égalité:
=
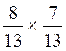Remarques
a) On peut multiplier plusieurs
fractions de même dénominateur ,il suffit de
multiplier les numérateurs entiers eux et les dénominateurs entre eux.
b)La procédure utilisée pour faire la
multiplication de deux fractions
s’applique à la multiplication de deux nombres écrit sous forme
d’écriture fractionnaire.
Par exemple : on
peut faire l’opération: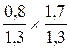 
qui donnera
Voici trois
cas :la soustraction s'opère de la même façon qu'avec
un nombre de dénominateur commun
|
Exemples
de calculs |
|
|
a)
Sans autre difficulté |
Il
est possible de développer (2x+1)2
Voir les IR : Réponses |
|
|
|
|
b ) idem |
|
|
|
|
|
c ) idem |
|
|
|
|
1°) Prendre 1/4 de la moitié de
200 € :
|
Calcul : On fera : Ce qui donne : |
Vérification : a) On prend la moitié de 200 €
= 100 € b) on calcule le quart de 100 €
= 100 /4 = 25 € On conclut : le quart de la moitié de 200 est 25. |
2°) Une balle tombe du premier étage (
solution : 2,50 fois ( 4 / 5 ) 5
TRAVAUX AUTO FORMATIFS
1° )Traduire en langage littéral: =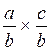 
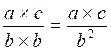
2°) Traduire en langage mathématique:
En
utilisant d’autres lettres que a ; b ; c )
3°) Donner la procédure permettant de faire la
multiplication de deux fractions de même dénominateur.
I:)
Effectuer les calculs suivants:
|
Exercices: |
Résultats |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II: ) Idem.
|
|
|
|
|
|
III )
Faire exercices avec des nombres décimaux relatifs
|
|
|
|
|
|
|
|
|
ALGEBRE
:Niveau IV :
Faire les multiplications suivantes
|
|
|
|
|
|
|
|
|
|
|
|
4°) Faire les
multiplications suivantes : algèbre
|
a ) |
|
|
|
b ) |
|
|
|
c ) |
|
|
|
d ) |
|
|
|
e ) |
|
|
Interdisciplinarité :
1°) Prendre 1/4
de la moitié de 200 € :
2°) Une balle tombe du premier étage (