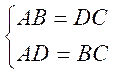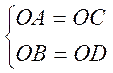|
|
|
|
|
|
|
|
ENVIRONNEMENT du
dossier:
|
1°) les angles
et les parallèles 2°) Le
parallélogramme en primaire. |
Suite :Le
parallélograme propriétés symétrie centrale …. |
|
|
|
|
|
|
3.
|
DOSSIER : LE
PARALLELOGRAMME
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.
Tracés. |
|
|
|
|
|
Collège : Travaux fiches sur : Le parallélogramme
( dont les propriétés)
|
|
|
Collège : Travaux fiches
sur : Le quadrilatère (dont les propriétés )
|
|
TEST |
COURS |
|
Interdisciplinarité |
|
COURS
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|||||||
|
|
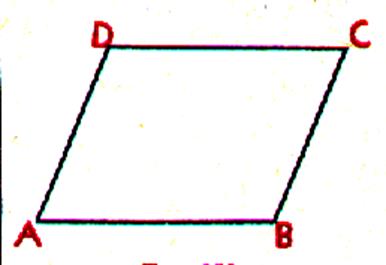
Un parallélogramme est un quadrilatère dont les cotés
opposés sont deux à deux parallèles. Exemple : AB et DC sont parallèles AD et BC sont parallèles |
|
|
|||||
|
|
|
|
||||||
|
|
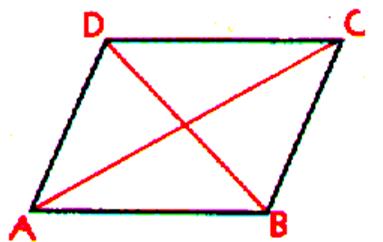
Les diagonales
sont les droites qui joignent les sommets opposés. DB et CA sont les diagonales du parallélogramme
DCBA. Un parallélogramme est un quadrilatère dont les
diagonales se coupent en leur milieu . |
|
|
|||||
|
|
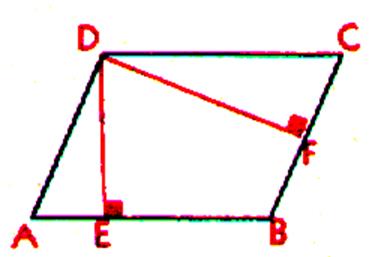
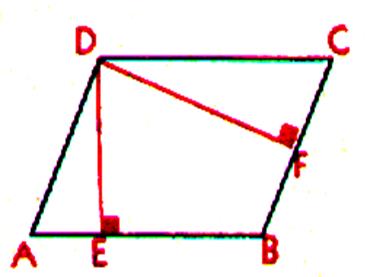
HAUTEURS : La hauteur
d’un parallélogramme est la distance de deux cotés parallèles
. Elle est déterminée par la perpendiculaire
commune à ces deux cotés. Un parallélogramme a deux hauteurs : La droite DE est la hauteur quand on prend AB comme base. La droite DF est la hauteur quand on prend BC comme base. |
|
|
|||||
|
|
Pour obtenir un parallélogramme il nous suffit de
superposer une bande à bords
parallèles sur une autre bande à bords parallèles dont la largeur est différentes de celle de
la première . La partie commune (en rouge) aux deux bandes est
un parallélogramme . |
|
|
|||||
|
|
|
|
||||||
|
|
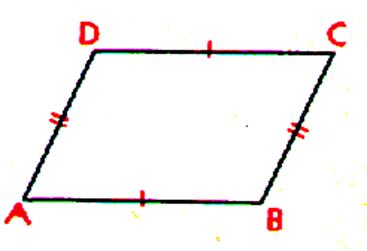
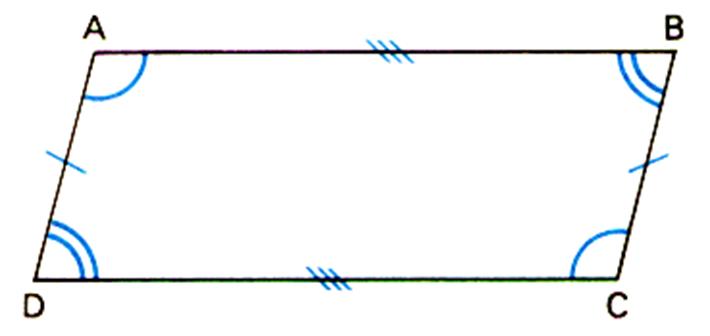
Première propriété : Dans un parallélogramme les cotés opposés
sont égaux : *Soit le parallélogramme DCBA. Décalquons le coté AD puis faisons
glisser le calque de façon que la point D se déplace sur le coté DC. Lorsque le point D coïncide avec le point C ,
le coté DA prend la direction CB , puisque
par un point , on ne peut mener qu’une
parallèle à une droite. Par ailleurs , nous constatons, lors du
déplacement du calque , que le point A se déplace constamment sur le coté AB , donc lorsque le point D coïncide avec le point
C , le point A coïncide avec le point B , puisqu’il doit se trouver à la fois
sur le coté AB et sur le coté
BC. Donc |
1°) un quadrilatère convexe
qui a ses cotés opposés égaux deux à deux est un
parallélogramme si AB= DC et AD =BC on peut conclure que AB
est parallèle à DC et que AD est parallèle
à BC 2°) un quadrilatère convexe qui a deux cotés et parallèles est un parallélogramme. si AB= DC et si AB
est parallèle à DC on peut
conclure que AD est parallèle à BC . |
|
|||||
|
|
Deuxième propriété : Dans un parallélogramme les angles opposés sont
égaux. Dans un parallélogramme DCBA
traçons la diagonale AC puis décalquons le triangle ADC . Déplaçons le calque sur le plan , de façon
que le point C vienne en A et le point
D en B. Nous constatons alors que le triangle ADC se superpose au triangle ABC
et qu’en particulier l’angle D se place
exactement sur l’angle B. Donc On peut vérifier de façon analogue que |
1° ) un quadrilatère dont les diagonales se coupent en leur milieu est un
parallélogramme .Si AO = OC et si BO =OD on peut conclure que AB est
parallèle à DC et AD est parallèle à BC Un quadrilatère convexe qui a ses angles opposés
égaux deux à deux et parallèles est un parallélogramme. Si |
|
|||||
|
|
Remarque : les angles adjacents à un même coté d’un
parallélogramme sont supplémentaires : ABCD étant un quadrilatère on peut écrire Or |
|
||||||
|
|
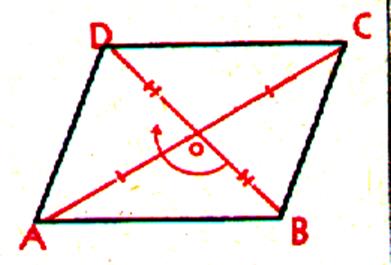
Dans un parallélogramme les diagonales se coupent
en leur milieu : Soit O le point d’intersection des diagonales AC
et BD .Décalquons le triangle AOB puis faisons tourner le calque de 180° autour du point
O ; nous constatons que le triangle AOB se superpose au triangle DOC :
en particulier OB coïncide avec OD et OA coïncide avec OC , Donc |
|
|
|||||
|
|
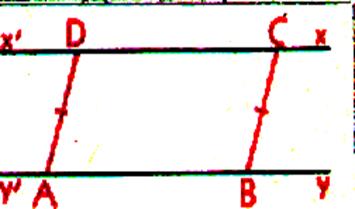
Remarque :
deux segments de droite parallèles compris entre deux parallèles sont égaux . Les segments de droites AD et BC qui sont compris
entre les parallèles x’x et y’y sont égaux : AD = BC |
|
|
|||||
|
|
|
|
|
|||||
|
|
IV) Parallélogramme et symétrie
centrale |
|
|
|||||
|
|
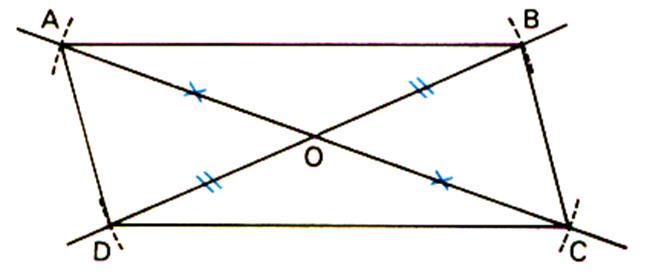
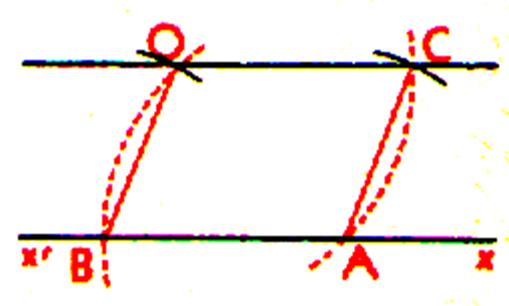
Un point O étant donné ,
traçons deux droites passant par O. Portons avec le compas sur chacune des deux
droites de part et d’autre du point O des longueurs égales. |
|
||||||
|
|
Par exemple :OA = OC = 5 cm ; OB = OD = Cette construction fait apparaître une symétrie
centrale SO telle que : SO : où
A à pour image C ; B à pour image
D ; C à pour image A ; D à pour image B . |
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
Activités : Si
nous mesurons les longueurs des côtés. Si nous mesurons les angles ,
nous en déterminons les propriétés suivantes : |
|
||||||
|
|
|
INFO : « Symétrie centrale
@ » |
|
|||||
|
|
|
|
||||||
|
|
D’après les propriétés des symétries centrales,
nous en concluons que : -
les côtés opposés
d’un parallélogramme sont parallèles. -
Les côtés opposés d’un
parallélogramme sont isométriques. -
Les angles
consécutifs d’un parallélogramme sont supplémentaires ; Les angles opposés d’un parallélogramme sont isométriques. |
|
||||||
|
|
|
|
|
|||||
|
|
RESUME : |
|
|
|||||
|
|
Dans un parallélogramme :
|
|
||||||
|
|
|
|
|
|||||
|
|
Ce qui suit est à retenir |
|
|
|||||
|
|
Définition : Le parallélogramme est un quadrilatère convexe
dont les côtés opposés sont parallèles
deux à deux . [DA ] // [ BC ] et [ AB] // [ CD ] (1) |
Propriétés : -les côtés opposés sont deux à deux
isométriques DA = CB et AB = DC
(2) -
les angles
opposés sont égaux deux à deux
-
deux angles
consécutifs sont supplémentaires (somme = 180°) -
les diagonales [ AC] et [ DB] se coupent en leur milieu (voir
+ : la symétrie centrale) (4) (5 ) deux côtés sont isométriques et parallèles |
|
|||||
|
|
Identification :quadrilatère ayant la propriété (1) ou (2) ou ( 3) ou ( 4) ou (5) |
|
||||||
|
|
|
|
|
|||||
|
|
5-
TRACES. Le tracé d’un parallélogramme sans contrainte de dimensions (angle et longueurs
des segments) ne pose pas de problème particulier. On trace deux droites
parallèles puis une droite sécante à ces deux droites puis
une droite parallèle à cette troisième droite. ► Identifier un parallélogramme : Remarque : on nomme un parallélogramme
par des lettres majuscules. Par convention, ces lettres sont lues dans le
sens des aiguilles d’une montre, le premier point nommé est celui qui se
trouve le plus en haut à gauche de la figure. Exemples : |
|
||||||
|
|
|
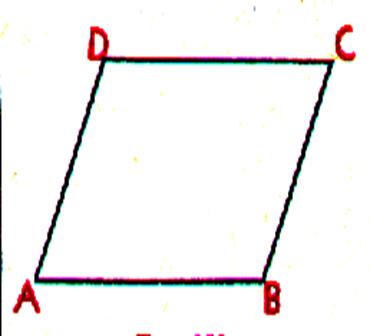
Parallélogramme (ABCD) |
|
|||||
|
|
|
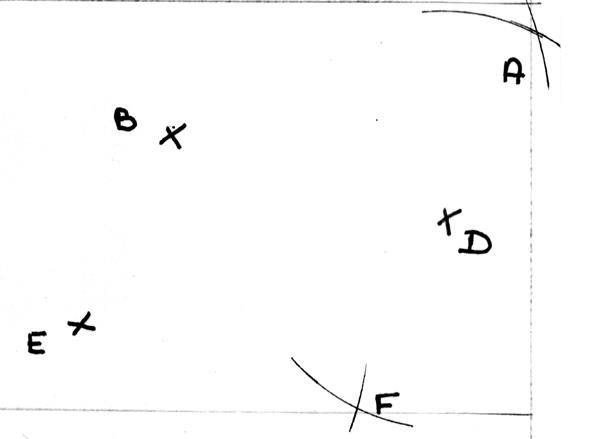
Dans la figure ci
contre je peut
identifier le parallélogramme (BADE) et le parallélogramme (BDFE) ( joindre les
points pour constater que nous avons bien deux parallélogramme.) |
|
|||||
|
|
|
|
|
|||||
|
|
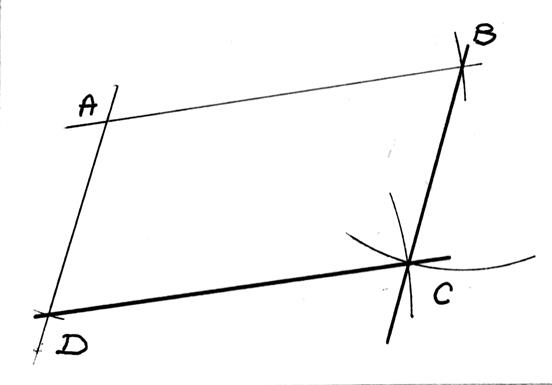
► CONSTRUCTION d’ un parallélogramme à partir d’une droite est
un point « O » extérieur à la droite |
|
||||||
|
|
Du point « O » comme centre
, avec un rayon plus grand que la distance de ce point à la droite x’x , on trace un arc de cercle qui coupe
cette droite au point A. Du point A comme centre , et avec le même rayon que
précédemment , on trace un second arc de cercle qui passe par « O »
et qui coupe la droite x’x au point B. Du point A comme centre ,
avec un rayon égal au segment OB , on trace un troisième arc , qui coupe le
premier en C : La droite OC est parallèle à la droite x’x . En effet : le quadrilatère convexe ABOC est
parallélogramme car il a ses cotés opposés égaux
deux à deux : On
a OA = OC ; OA =BA donc OC = AB
et OB = AC donc AB et OC sont parallèles . |
|
|
|||||
|
|
|
|
|
|||||
|
|
Voir d’autres tracés : Recherche du quatrième sommet d’un parallélogramme avec un compas. ►à partir de deux droites sécantes. ►à partir de trois points. Ces types de tracés vont
être utiles lorsque l’on cherchera à tracer un bipoint équipollent à
un bipoint donné. Pour comprendre la définition d’un vecteur et la translation d’un vecteur dans un plan. En vue de faire la somme de
plusieurs vecteurs. |
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
TRAVAUX AUTO FORMATIFS
CONTROLE :
(6ème) 1 ) Donner la définition d’un parallélogramme :
(5ème) 2 ) Citer
les trois principales propriétés d’un parallélogramme.
EVALUATION
1°) construire un parallélogramme , sachant que deux côtés consécutifs mesurent
respectivement
Calculer les autres angles de ce parallélogramme .
2°) construire sans rapporteur un parallélogramme ,
sachant que ses deux diagonales mesurent respectivement
3°)Construire un parallélogramme dont les côtés mesurent respectivement
4°) Construire sans rapporteur un parallélogramme ,
sachant que le côtés AB mesure
5° ) Construire un parallélogramme ABCD , sachant
que le côté AB mesure
|
1. Parallélogramme ABCD de côtés
AB = |
|
|
2. Parallélogramme ABCD tel que AB
= |
|
|
3. Parallélogramme ABCD de côté AB
= 5cm et de diagonales AC = |
|
|
4. Parallélogramme ABCD tel que AB
= 2,5cm et AD = 5cm et la diagonale AC = |
|
|
5. Parallélogramme ABCD de côtés AB = 5cm et AD = 4cm et de hauteur AH = 3cm |
|
|
6. Parallélogramme ABCD de côté AB= |
|
INTERDISCIPLINARITE