Géométrie : DOSSIER : TRACES GEOMETRIQUES/ / Objectif de base

Pré requis:

Projection orthogonale d'un point et distance .
Droite

Environnement du cours :

Index warmaths

Précédent 1°) Premiers tracés 2°) les parallèles

Objectif suivant 1°) les quadrilatères

tableau liste des cours sur la géométrie plane .

Droites parallèles «le  tracé d’une droite parallèle à une autre droite »

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité Travaux Dossier 68 - 69

Corrigé Contrôle

Corrigé évaluation

COURS:

Tracé N°1
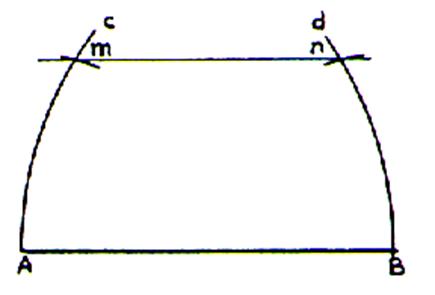
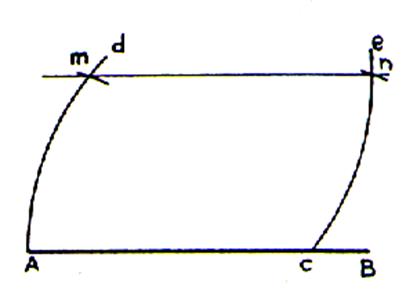
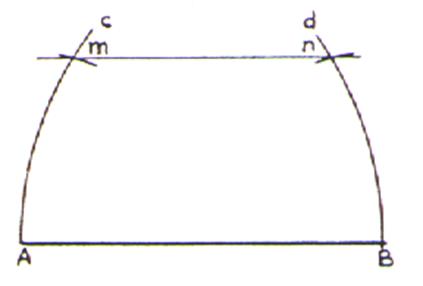
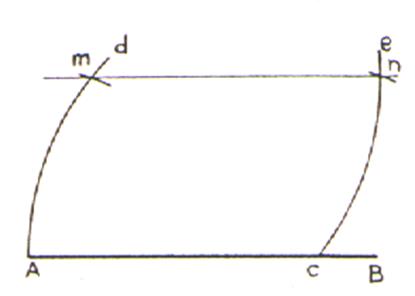
Tracer un segment AB. Avec un compas , prendre A comme centre , tracer un arc de cercle « d » ; prendre comme centre B et tracer un arc C ( de rayon AB) . Prendre comme centre le point A , avec le compas placer le point « m » ; aller en B , en conservant la même ouverture Am ; placer le point « n ». Tracer une droite passant par m et n . Cette droite est mn est parallèle à AB

Tracé N°2
Tracer une droite AB .. Avec un compas , prendre comme centre « c » tracer un arc de cercle « d » , prendre A comme centre coupant l’arc « d » en « m ». Prendre comme centre « m »  tracer un arc de cercle de rayon « mc » appelé « e » Prendre avec le compas l’ouverture « Am » , prendre « c » comme centre et ensuite tracer le point n . Tracer la droite passant par les points « m » et  « n ».

Tracé N°3
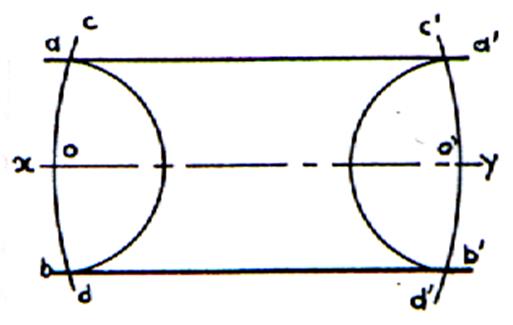
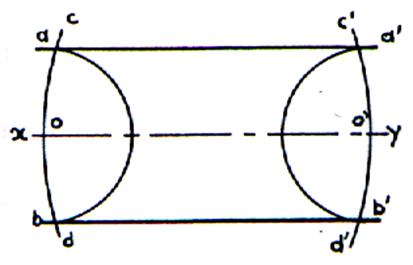
En partant d’un axe . On trace des parallèles à l’axe « x ;y »

Tracé N°4
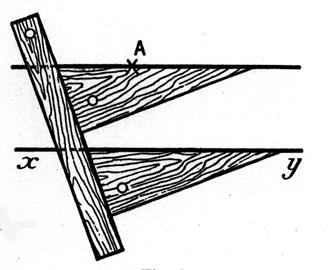
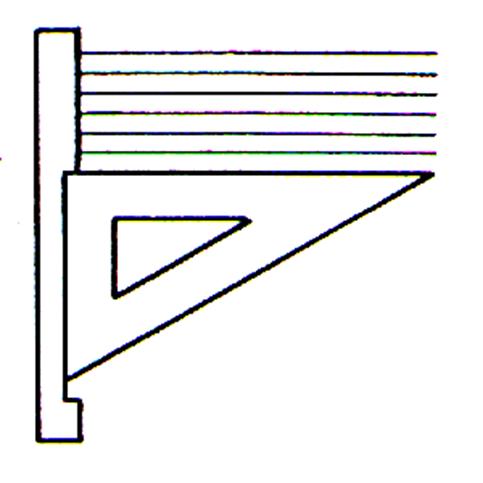
Autre façon d’obtenir des droites parallèles : Avec un té ou une règle entaillée et une équerre . (en fait on trace des droites perpendiculaires à la règle ou té )

Tracé N°5 : avec le rapporteur…….	Tracé N°6 : on pace trois points , trouver la position du quatrième pour obtenir les pôles d’un parallélogramme……
Tracé N°7 Parallèle à une droite donnée passant par un point donné ou à une distance donnée	Réf. CAP TC2 E4 / 6^e Info plus :projection orthogonale et distance entre 1 point et une droite.
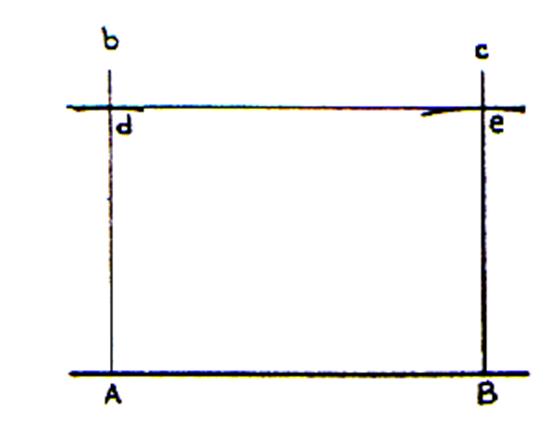
A un point donné Ld) Soit une droite donnée Tracer une perpendiculaire passant par « d ».coupant la droite en « A » En un autre point de la droite donnée , placer un point « B ». Tracer une perpendiculaire à « B » Avec un compas reporter la distance qui lit « d » à « A » Sur la droite perpendiculaire en B.(point « e ») Tracer une droite passant par « d » et « e » A une distance donnée Tracer une droite AB : Tracer une perpendiculaire en A et en B Avec une règle graduée , placer les points « d » et « e » . Tracer une droite passant par ces deux points

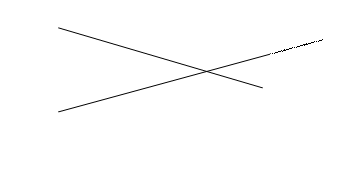
Remarque : Les droites sécantes ne sont pas parallèles

Elles ont un seul point commun, qui est le lieu où les deux droites se rencontrent!

II ) Théorèmes sur les positions relatives de deux droites parallèles et une troisième droite :

Théorème1 : Si deux droites sont parallèles , toute droite parallèle à l’une est parallèle à l’autre

Théorème 2 : Si deux droites sont parallèles , toute sécante à l’une est sécante à l’autre.

Théorème 3 : Si deux droites sont parallèles , toute perpendiculaire à l’une est perpendiculaire à l’autre.

Travaux auto formatifs.

CONTROLE  :

citer les trois théorèmes relatifs aux positions relatives de deux parallèles et d’une troisième droite .

EVALUATION :

Refaire les tracés suivants , donner la procédure.

Tracé N°1

Tracé N°2

Tracé N°3