|
|
|
|
|
Corrigé
du devoir auto formatifs :LES INTERVALLES :
(Représentation graphique et ses limites)
|
|
|
|
|
Interdisciplinarité
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|||||||
|
|
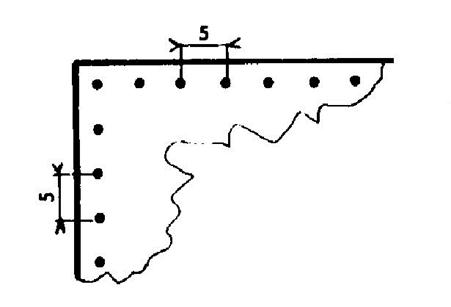
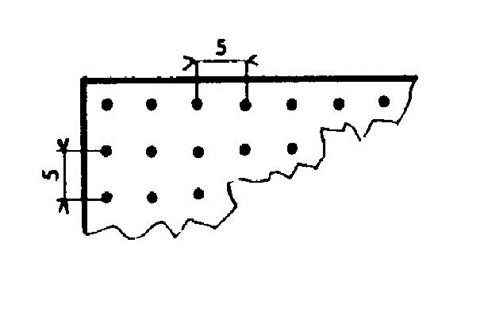
TRAVAUX AUTO FORMATIFS : CONTROLE : 1°) Qu’est qu’un intervalle ? La distance entre deux objets est appelée « intervalle » 2°) Citer les 4 cas qui peuvent être traités avec les intervalles. Cas de la ligne fermée : -
Nombre
d’objets ( d’arbres)
= nombre d’intervalles. Cas d’une ligne non fermée : Voir : - des objets aux deux extrémités. -
Un objet à une seule extrémité. - pas d’objet aux extrémités. EVALUATION I ) Le service des espaces verts veut border un espace rectangulaire de 924 m sur 728 m de large à l’aide
d’arbustes régulièrement espacés. Un arbuste sera planté à chaque angle du
terrain. La distance entre deux arbustes est de 5
mètres. Déterminer, le nombre d’arbustes à planter . CORRIGE : I ) Le service des espaces verts veut border un espace rectangulaire de 924 m sur 728 m de large à l’aide
d’arbustes régulièrement espacés. Un arbuste sera planté à chaque angle du
terrain. La distance entre deux arbustes est de 8
mètres. Déterminer, le nombre d’arbustes à planter . Longueur plantée : 2 ( 924 + 728 ) = 3304 Nombre d’arbustes : 3304 : 8 =
413 arbustes Si l’écart est de 5 m alors : on
planterait 3304 : 5 = 660,8 cela ne tombe pas juste
. Il faudrait répartir les
0,8 fois 5 m = 4 m entre les 660 arbustes pour avoir la
distance entre les deux arbustes. II ) Le service des espaces verts
veut border un espace rectangulaire
de 924 m sur 728 m de large à l’aide d’arbustes régulièrement espacés.
Un arbuste sera planté à chaque angle du terrain. La distance entre deux arbustes doit être un nombre entier de mètres. 1°) Déterminer
toutes les valeurs possibles de la distance entre 2 arbustes. 2°) Déterminer, dans chaque cas le nombre
d’arbustes à la plantation. II ) Le service
des espaces verts veut border un
espace rectangulaire de 924 m sur 728
m de large à l’aide d’arbustes régulièrement espacés. Un arbuste sera planté
à chaque angle du terrain. La distance entre deux arbustes doit
être un nombre entier de mètres. 1°) Déterminer toutes les valeurs possibles de la distance
entre 2 arbustes. 3304 : n = D
; D : distance entre
deux arbustes est un nombre entier. On décompose en produit de facteurs
premiers = 2 fois 2 fois 2 fois 7 fois
59 2°) Déterminer, dans chaque cas le
nombre d’arbustes à la plantation. 2 ; 4 ; 8 ; 56 ; 14 ,
28 , et 2 fois 59 , 4 fois 59 ; 8
fois 59 , 14 fois 59 ; 28 fois
59 ; |
||||||||
|
|
|
|
|||||||
|
|
Autres Applications :SITUATIONS PROBLEMES : |
|
|
|
|
Situation Problème n°1 : |
|
|
|
|
Un champ a la forme d’un carré de 75 m de côté. A « 2,5m » du bord de ce champ ( à l’intérieur), on plante une rangée d’arbres. Ces arbres sont alors situés sur le pourtour d’un
carré. Il y a un arbre à chaque sommet. Quel est le nombre d’arbres ? |
|
|
|
Nombre d’arbres par ligne : ( voir
le « cas 1 » ) a)
Sur une
ligne : Nombres d’intervalles ( n ) :
n= 75 / 5 = 15 b)
Sur une
ligne : Nombre d’arbres :
« n – 1 » = « 15
– 1 » = « 14 » arbres par ligne. c)
Nombres de
lignes ( de 14 arbres J ) = voir le calcul ci-dessus = on compte
14 lignes de 14 arbres. d)
Nombres
total d’arbres = 14 fois 14 = 196 arbres |
|||
|
|
|
||
|
Situation Problème n°2 : |
|
||
|
Dans un champ rectangulaire dont les longueurs
des côtés sont « 95 m » et « 40 m », on veut planter des
arbres d’une même rangée sont distants de s
« 5 m » et ils sont
situés à « 2, 5 m »du bord. Combien d’arbres peut-on planter ? |
|
||
|
|
Nombre d’arbres par ligne : ( voir
le « cas 1 » ) Nombre d’arbres sur la longueur : ( 95 / 5 ) –
1 =
19 – 1 = 18 arbres. Nombre se lignes de 18 arbres (sur
la largeur) = ( 40
/ 5 ) – 1 = 7 lignes de 18 arbres . Nombre d’arbres plantés : 18 fois 7 = 126 arbres. |
|
|