|
Les Segments « bornés » |
|
|
|
ENVIRONNEMENT
du dossier:
|
Objectif précédent |
2°) Les
espacements !.......... |
(Représentation graphique et ses limites)
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
COURS :
|
Première
approche :
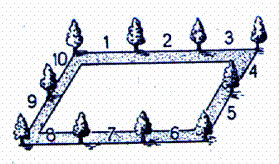
tracer une ligne droite
, un carré , un cercle ou toute autre ligne fermée , montrer
que dans le premier cas si on divise la lignes en parties égales et si on met
un objet (arbre , piquet de clôture ,
borne kilométrique ) , alors qu’à chaque bout le nombre des objets est
supérieur d’une unité à celui des intervalles
(intervalle = espace entre deux objets ) |
|
|
Si au
contraire on ne met rien aux deux extrémités , le
nombre des espaces est supérieur d’une unité à celui des objets. |
|
|
et si
l’on met seulement à une extrémité , il y a autant
d’objets que d’intervalles |
|
|
et si
l’on met chaque extrémité un objet , il y a un objet de plus que d’intervalles |
|
|
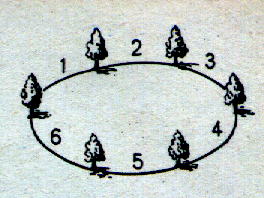
Dans tout
« cycle » fermé , polygone , cercle
ellipse , le nombre des espaces est égal au nombre des divisions . Il y a
autant d’objets que d’intervalles . |
|
|
|
|
1°) Qu’est qu’un
intervalle ?
2°) Citer les 4 cas qui peuvent être traités avec les
intervalles.
I ) Le service des espaces verts veut border un espace rectangulaire de 924 m sur 728 m de large à l’aide d’arbustes
régulièrement espacés. Un arbuste sera planté à chaque angle du terrain.
La distance entre deux arbustes est de 5
mètres.
Déterminer, le nombre d’arbustes à planter .
II ) Le
service des espaces verts veut border un
espace rectangulaire de 924 m sur 728 m
de large à l’aide d’arbustes régulièrement espacés. Un arbuste sera planté à
chaque angle du terrain.
La distance entre deux arbustes doit être un nombre entier de mètres.
1°) Déterminer toutes
les valeurs possibles de la distance entre 2 arbustes.
2°) Déterminer, dans chaque cas le nombre d’arbustes à la
plantation.
CORRIGE :
I ) Le service
des espaces verts veut border un espace
rectangulaire de 924 m sur 728 m de large
à l’aide d’arbustes régulièrement espacés. Un arbuste sera planté à chaque
angle du terrain.
La
distance entre deux arbustes est de
8 mètres.
Déterminer,
le nombre d’arbustes à planter .
Longueur
plantée : 2 ( 924 + 728 ) = 3304
Nombre
d’arbustes : 3304 :
8 = 413 arbustes
Si
l’écart est de 5 m alors : on planterait
3304 : 5 = 660,8 cela ne tombe
pas juste .
Il
faudrait répartir les 0,8 fois 5 m
= 4 m entre les 660 arbustes pour
avoir la distance entre les deux arbustes.
II ) Le service des espaces verts veut border un espace rectangulaire de 924 m sur 728 m de large à l’aide
d’arbustes régulièrement espacés. Un arbuste sera planté à chaque angle du
terrain.
La
distance entre deux arbustes doit être
un nombre entier de mètres.
1°)
Déterminer toutes les valeurs possibles
de la distance entre 2 arbustes.
3304 :
n = D
; D : distance entre
deux arbustes est un nombre entier.
On
décompose en produit de facteurs premiers =
2 fois 2 fois 2 fois 7 fois 59
2°)
Déterminer, dans chaque cas le nombre d’arbustes à la plantation.
2 ;
4 ; 8 ; 56 ; 14 , 28 ,
et 2 fois 59 , 4 fois 59 ; 8 fois
59 , 14 fois 59 ; 28 fois 59 ;