CORRIGE cours 1 : LES INTERVALLES Représentation graphique et ses limites

CONTROLE :

1°) Qu’est qu’un intervalle ?

2° )Que signifie les écritures suivantes :

Sur une droite graduée (munie d’un repère (O, I) , on peut définir pour tout couple de points A et B , d’abscisses respectives « a » et « b ».plusieurs formes d’intervalle .	Si on désigne par « x » tous les nombres appartenant à l’intervalle et par « a » et « b » les bornes (ou limites)
Que désigne les écritures ci dessous ?	Montrer la notation
Un intervalle fermé noté : [A B]	Notation : a…≥ x …≤ b… Exemple :
Un intervalle ouvert noté : ] A B [	Notation : a…< x < …b… Exemple :
Un intervalle fermé à gauche , ouvert à droite , noté : [A B[	Notation : .a…≥ x <…b… Exemple :
Un intervalle ouvert à gauche , fermé à droite , noté : ]A B]	Notation : …a ..< x ≤…b… Exemple :

EVALUATION

A partir des tracés : NOMMER chaque intervalle et donner sa notation sous la forme  d’un encadrement : ? X ?

Remarque : L’intervalle considéré est représenté par le segment de droite « bleu » en trait fin…..

INTERVALLE FERME

+4 ≥ x ≤ +15 

.

I

[ ]

+4

+15

O

INTERVALLE OUVERT

Notation : +4 < x < +15

..

I

: ] [

+4

+15

O

INTERVALLE OUVERT à gauche , fermé à droite

On le notera + 4 < x ≤ + 15 ; on lira les valeurs de « x » sont comprises entre + 4 « exclus » et +15 « inclus »

I

: ] ]

+4

+15

O

INTERVALLE OUVERT à droite , fermé à gauche

Notation : +4 ≥ x < +15 ; on lira les valeurs de « x » sont comprises entre + 4 « inclus » et +15 « exclus »

I

: [ [

+15

+4

O

Faire une représentation graphique :

+4 ≥ x ≤ +15 

+4 ≥ x < +15

+4 < x < +15

+4 < x ≤ + 15

,

INTERDISCIPLINARITE

Cours 2 : appliqué

Applications :SITUATIONS PROBLEMES :
Situation Problème n°1 :
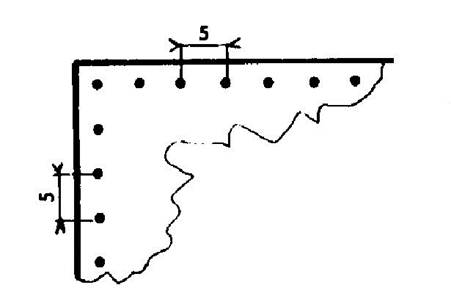
Un champ a la forme d’un carré de 75 m de côté. A « 2,5m » du bord de ce champ ( à l’intérieur), on plante une rangée d’arbres. Ces arbres sont alors situés sur le pourtour d’un carré. Il y a un arbre à chaque sommet. les arbres consécutifs sont distants de « 5 m ». Quel est le nombre d’arbres ?
Nombre d’arbres par ligne : ( voir le « cas 1 » ) a) Sur une ligne : Nombres d’intervalles ( n ) : n= 75 / 5 = 15 b) Sur une ligne : Nombre d’arbres : « n – 1 » = « 15 – 1 » = « 14 » arbres par ligne. c) Nombres de lignes ( de 14 arbres J ) = voir le calcul ci-dessus = on compte 14 lignes de 14 arbres. d) Nombres total d’arbres = 14 fois 14 = 196 arbres
Situation Problème n°2 :
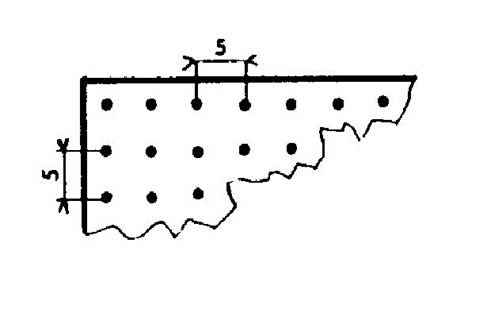
Dans un champ rectangulaire dont les longueurs des côtés sont « 95 m » et « 40 m », on veut planter des arbres d’une même rangée sont distants de s « 5 m » et ils sont situés à « 2, 5 m »du bord. Combien d’arbres peut-on planter ?
Nombre d’arbres par ligne : ( voir le « cas 1 » ) Nombre d’arbres sur la longueur : ( 95 / 5 ) – 1 = 19 – 1 = 18 arbres. Nombre se lignes de 18 arbres (sur la largeur) = ( 40 / 5 ) – 1 = 7 lignes de 18 arbres . Nombre d’arbres plantés : 18 fois 7 = 126 arbres.