|
|
|
ENVIRONNEMENT du
dossier:
|
Objectif précédent :: 1°) le rectangle activités découvertes.
2°) Fiche découverte
collège des propriétés du rectangle. (P6) |
Les autres
parallélogrames. |
2.
Liste
des cours de géométrie.. 3.
Fiches activités de géométrie (à consulter) |
|
|
|
|
|
|
DOSSIER : LE RECTANGLE (caractéristiques)
|
|
1°)
Notion « découverte » |
|
|
|
2°)
Définition: |
|
|
|
3°) Les
PROPRIETES ( rappels : les propriétés d’un quadrilatère et les propriétés
spécifique aux rectangle.) |
|
|
|
4°) Caractères permettant de reconnaître
qu'un parallélogramme est un rectangle. |
|
|
|
5° )
Tracé d’un
« rectangle ». |
|
|
|
6°) Calcul de la Diagonale
d’un rectangle. |
|
|
|
7°) Résumé
« à retenir » sur les rectangles . |
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
COURS
|
1°) Notion « découverte » du rectangle : Intersection de deux
bandes de papier d'inégale largeur,
placées perpendiculairement, forment un parallélogramme particulier : le
rectangle. |
|
|
2°) Définition: |
|
|
Un rectangle est un parallélogramme qui a un angle droit. |
|
|
3°) Les PROPRIETES |
Le rectangle étant un parallélogramme particulier ,
possède toutes les propriétés du parallélogramme, plus certaines propriétés
qui lui sont particulières |
|
Rappels : Propriétés communes avec le
parallélogramme: 1°) les cotés opposés
sont égaux. 2°) les angles opposés
sont égaux. 3°) les angles
adjacents à un même coté sont supplémentaires. 4°) les diagonales se
coupent en leur milieu. |
|
|
Les Propriétés
particulières au rectangle: |
|
|
1°) les angles consécutifs sont des angles
droits.
En effet nous savons que:
donc par ailleurs , nous savons que:
donc |
|
|
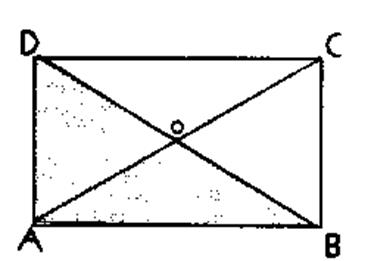
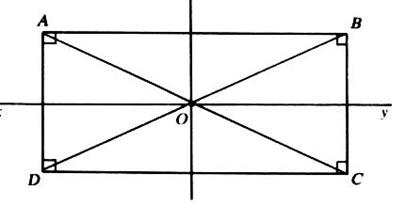
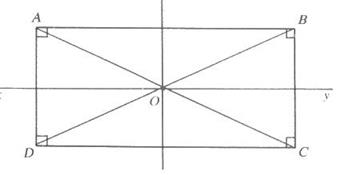
2°) les diagonales sont égales: Soit AC et BD les diagonales .Décalquons le
triangle ADB , retournons le calque de façon que le coté
AD vienne se placer sur le coté BC. Nous constatons que le triangle ADB vient se
placer sur le triangle ABC et qu'en particulier l'hypoténuse BD coïncide avec
l'hypoténuse AC. Donc AC =
BD Conséquence: OA = OB =
OC = OD |
|
|
4°) Caractères permettant de
reconnaître qu'un parallélogramme est un rectangle: |
|
|
1) un parallélogramme qui a ses diagonales égales
est un rectangle. |
|
|
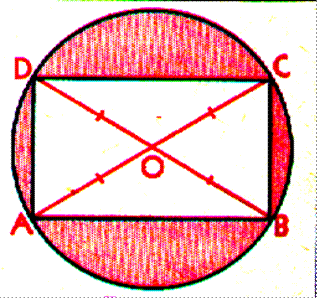
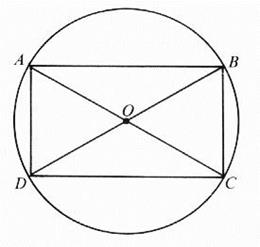
2)Cercle circonscrit: Soit "O" le point d'intersection des
diagonales d'un rectangle. Si du point "O" comme centre nous
décrivons une circonférence qui a pour
rayon OA , cette circonférence passe par les quatre
sommets du rectangle; c'est le cercle circonscrit à ce rectangle. Remarques: 1) OA = OC = 2)le cercle est circonscrit au triangle ACB et au triangle
ADC. |
|
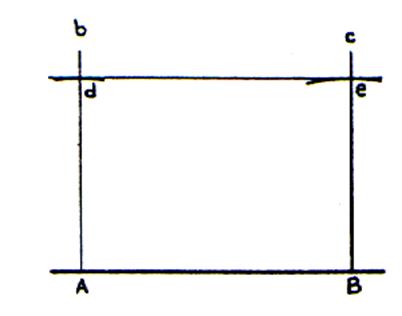
5° ) Tracé d’un « rectangle »
|
( voir : « tracés de parallèles » et
« tracés de perpendiculaires ») |
|
Tracer une droite Placer le points A et B . Tracer de perpendiculaires à A et B.(droites « b » et « c ») Avec un compas placer les points « d » et « e » Tracer une droite passant par les points « d » et
« e » |
|
|
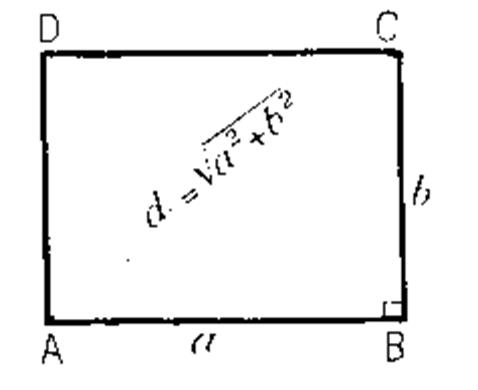
6°) Calcul de la Diagonale d’un rectangle |
|
|
D' après " Pythagore" : La diagonale au carré "d²" est égale à AC²
= AB² + BC² |
|
|
|
7°) Résumé
« à retenir » sur les
rectangles : |
|
||||||
|
|
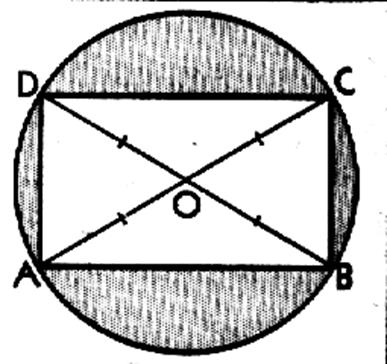
Définition : On appelle rectangle , un
parallélogramme ayant un angle droit .
Propriétés : Nous admettrons
qu'il en est ainsi , uniquement dans le cas
où les diagonales [ AC ] et [ DB] ont
la même longueur . Il en résulte que dans un rectangle ABCD les
quatre angles sont droits :
Les côtés
opposés sont parallèles et ont
la même longueur :
AB = CD et AD
= BC Le point de concours des diagonales est
équidistant des quatre sommets . Il existe donc un cercle circonscrit au rectangle et son
centre est le point de concours des diagonales . OA = OA = OC = OD .
D1
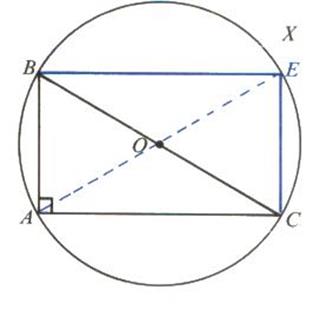
*Remarque : Soit le rectangle BECA ; La figure BCA et la figure BEC sont des demi -
rectangles. On les appelle "
triangle rectangle", l'un est "rectangle" en A , l'autre est
"rectangle" en E . (les diagonales sont appelées : "hypoténuse" )
|
|
||||||
|
|
|
|
CONTROLE :
Quelles sont les caractéristiques ( propriétés ) du rectangle
?
EVALUATION
Tracer :
|
1°) Rectangle ABCD tel que AB = 55mm et AD = 35
mm |
|
|
2°) Rectangle ABCD de diagonale 5 cm et de côté
AB = 20 mm |
|
|
3°) En +++ : Rectangle ABCD de diagonale 55 mm et tel que |
|
|
4°) En
plus : rectangle ABCD de longueur triple de la largeur et de périmètre
16 cm . |
|