|
Pré requis : |
|
|
Rappels sur les
ensembles de nombres :
N ; Z ; D ;R ; |
|
|
Ce qu’il faut savoir sur : le nombre relatif |
|
|
Opposé d' un nombre relatif |
|
|
|
|
|
Les relations d ’ ordre |
|
|
Représentation graphique des nombres relatifs positifs et
négatifs. |
|
|
Rappels : Construction d’ un axe gradué |
|
|
Classification des nombres décimaux relatifs |
|
|
Opérations avec les nombres
décimaux relatifs |
|
|
DOSSIER
"résumé "
Liste des opérations de base avec des Réels
Informations :
Ci-dessous :
RESUME du cours sur les opérations avec les nombres relatifs sur les 4
opérations avec les nombres relatifs ;
I ) ADDITION : (SOS cours)
a) La somme de deux réels de même signe est un
autre réel ayant :
pour signe :
le signe commun
pour valeur absolue : la
somme des valeurs absolues.
Exemples 5,2 + 3,51 = 8,71 ;
- 2,5 - 6,4 = - 8,9
b) La somme
de deux réels de signes contraires est un autre réel ayant :
pour signe : le signe du nombre qui a la plus grande valeur absolue
pour valeur absolue :la
différence des valeurs absolues ( la plus grande moins la plus petite )
Exemples : -12,7 + 6,5 = - 6,2 ;
0,13 - 4,25 = -4,12
II ) MULTIPLICATION : SOS cours
Le produit de deux réels est un autre réel qui a :
pour signe : + si les réels
sont de même signe
- si les réels sont de signe
contraires.
Pour valeur absolue : le produit des valeurs
absolues.
Exemples : 2 ![]() 3,4 =6,8 ; (-1,1 )
3,4 =6,8 ; (-1,1 ) ![]() (-3) = 3,3 ; 3
(-3) = 3,3 ; 3 ![]() (-8) = -24
(-8) = -24
III ) LA SOUSTRACTION
Remarquer que la soustraction ne se fait pas SOS
info
« il suffit d’ajouter au premier nombre l’opposé du second »
IV ) DIVISION : SOS cours
Le quotient d’un réel par un réel est un autre réel
qui a :
pour signe : + si les réels sont de même signe
- si les réels sont de signe
contraires.
Pour valeur absolue : le quotient des valeurs
absolues.
Exemples : ![]() = 1,1 ;
= 1,1 ; 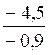 = 5 ;
= 5 ; 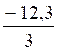 = - 4,1 ;
= - 4,1 ; ![]() = - 3
= - 3
Travaux :
Citer les règles de calcul concernant les
nombres « réels »
|
Devoir N°2 ( batterie d’exercices) |
|
|
Devoir N°3 |
|
|
Devoir
interdisciplinarité |