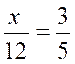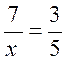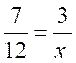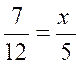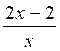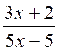|
|
|
|
|
|
|
|
|
|
Voir: transformer
N en fraction équivalente à une autre fraction dont on impose un dénominateur. |
|
environnement
|
Objectif précédent : |
Objectif suivant : |
Liste des cours en
calcul numérique |
DOSSIER : transformation d’une fraction en fraction équivalente .
FRACTION EQUIVALENTE à une autre fraction dont le dénominateur est donné.
|
COURS |
Interdisciplinarité |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Définition
de l ‘ objectif : Savoir construire une
fraction égale à une fraction donnée .dont le dénominateur est donné.
On sait que deux fractions séparées par le
signe « égal » sont dites
« fractions équivalentes »
Modèle
mathématique à utiliser:
![]() =
=![]() (b et d sont différents de 0)
(b et d sont différents de 0)
a / b est la fraction ,
d est le dénominateur donné
(le nouveau dénominateur )
pour Calculer "x" : voir le produit en croix
Exemple
numérique:
On donne la fraction ![]() ;la transformer en
fraction équivalente de dénominateur valent 20
;la transformer en
fraction équivalente de dénominateur valent 20
PROCEDURE :
a) On
pose :
![]() =
=![]() ( voir comment on
vérifie : page........)
( voir comment on
vérifie : page........)
b ) On transforme : 20 fois ![]() = x
= x
|
voir
multiplication d'un nombre par une fraction |
c) on
calcule :![]() fois
fois![]() = x
; 80
= x
; 80
d)Conclusion: La fraction ![]() est équivalente à la fraction
est équivalente à la fraction
![]()
e)
Vérification:
on
calcule : 48
fois 20=
on calcule 12
fois 80 =
On compare et l'on conclut :
Si les produits sont identiques , les
fractions sont équivalentes !
TRAVAUX AUTO
FORMATIFS.
1° ) Donner la procédure permettant d'obtenir
une fraction équivalente à une fraction donnée mais dont on impose le
dénominateur.
1° ) Donner la fraction équivalente à la fraction donnée , le
dénominateur étant fixé:
|
Fraction |
Dénominateur de la fraction
équivalente vaut |
|
|
|
|
|
20 |
|
|
|
|
|
75 |
|
|
|
|
|
100 |
|
|
|
II ) On peut transformer , par le
produit en croix , pour obtenir des fractions équivalentes , faire l' exercice qui correspond à la
situation:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III)
Donner la fraction équivalente à la fraction donnée ,
le dénominateur étant fixé:
|
|
Dénominateur imposé: |
|
|
|
-12 |
|
|
|
|
|
|
|
2y2 |
|
|
|
1,5yx |
|
|
|
X2 |
|
|
|
(5x-5)2 |
|
|
|
|
|
INTERDISCIPLINARITE : Applications : en sciences , LES PROPORTIONNALITES