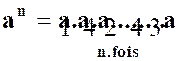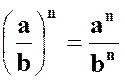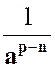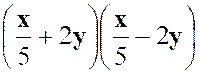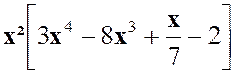L’algèbre est
une langue d’une admirable clarté qui
n’a pas de signe pour exprimer les notions confuses et procure à la pensée une
véritable économie . ( FOURNIER (1768-1830))
2.
Le calcul algébrique avec deux
nombres relatifs.
3.
Retour vers : la multiplication en algèbre…
|
|
Objectif
précédent : 1. Notions
préliminaires en calcul numérique.
2. Algèbre : Notions
préliminaires 3. Compléments d’informations sur le vocabulaire : ·
Cours 1 … ; Cours 2 …. ;
Cours 3 .. ; Cours 4 …. |
Objectif
suivant : ·
Retour vers la liste des cours : la calcul algébrique ( généralités). |
|
|
|
|
|
3.
|
Calcul algébrique :
résumé LES PRODUITS
|
|
|||||||||
|
|
1 ) Propriétés des
puissances entières. |
|
|||||||
|
|
1-1 :
Puissance d’un produit de facteurs , ou d’un quotient. |
|
|||||||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
||||||||
|
|
1-6 :
Cas particuliers fondamentaux : les produits
remarquables |
|
|||||||
|
|
1 – 7 : Différence de deux carrés. |
|
|||||||
|
|
1 – 8 La mise en facteur commun. |
|
|||||||
|
|
|
||||||||
|
|
|
|
|||||||
|
2 ) La décomposition
en produit de facteurs et son rôle
essentiel. LA FACTORISATION. ( voir les 27 exercices types) |
|
||||||||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
||||||||
|
|
2 – 4 : Intervention des différences de deux
carrés seules . |
|
|||||||
|
|
2 – 5 : souvent la différence de deux
carrés ne sont pas en évidence et il y
a lieu de les faire apparaître
, notamment par application des identités fondamentales du chapitre 1-6 |
|
|||||||
|
|
2 – 6 Intervention
des différences de deux carrés , combinées avec la
mise en facteur commun. |
|
|||||||
|
|
|
||||||||
|
|
|
|
|||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
COURS |
|
Interdisciplinarité : voir les études de
fonctions
|
|
|
|
||||
|
Commentaire : Ce
résumé destiné aux élèves de lycée (niveau 4 ) ne sera entièrement compris que si l’on maîtrise
les cours sur les
( ou le J
« nombres relatifs ») |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
1 )Propriétés
des puissances entières. |
|
|||||||||||||||||||
|
|
Tous les exposants utilisés ,ici, sont entiers et positifs. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Remarques : a)
Toute puissance d’un
nombre positif est un nombre positive. b)
Toute puissance
« paire » d’un nombre négatif est un nombre positif : exemple : ( - 2 ) 4 = +
16 c)
Toute puissance
« impaire » d’un nombre négatif est un nombre négatif : exemple : ( - 2 ) 7
= - 128 |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
· 1-1 : Puissance d’un produit de facteurs , ou d’un quotient. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
· 1-2 Produit de puissances
d’un même nombre. |
|
||||||||||||||||||
|
|
c’ est la règle de l’addition des
exposants.. Pour l’application de cette règle, si une lettre
n’a pas d’exposant, il faut lui affecter l’exposant « un » ( exposant :
1 )
Cette
règle ne s’applique qu’aux produits de puissances ; S’il y a
plusieurs lettres dans le produit envisagé, on applique la règle à chacune
d’elles : Ainsi : |
|
||||||||||||||||||
|
|
· 1 - 3 Elévation d’une puissance
à une puissance. |
|
||||||||||||||||||
|
|
On multiplie les exposants :
Exemples : |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
· 1-4 Quotient de deux puissances d’un même
nombre. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Soit : |
|
|
|
||||||||||||||||
|
|
L’introduction de la notation des exposants négatifs évite de
distinguer les trois cas. ON convient que :
On a alors dans tous les cas : Exemples : |
|
||||||||||||||||||
|
|
|
Pour « p = n » on aurait |
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
· 1- 5 Propriété distributive
ou « distributivité ». |
|
||||||||||||||||||
|
|
La multiplication est distributive relativement à
l’addition algébrique. Il s’agit de la multiplication d’une somme
algébrique par un terme ou par une « autre » somme algébrique. Il faut tenir compte éventuellement de la
« règle des signes »…..(voir ci-dessus) |
|
||||||||||||||||||
|
|
|
( a + b – c ) .
n =
n a + nb
– n c ( a + b – c ) ( n – p
) =
n a + nb
– n c – pa – pb + pc |
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||
|
· 1 – 6 Cas particuliers fondamentaux :
les produits remarquables . |
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
( a + b ) ² = a² + 2 ab + b² ( a - b ) ² = a²
- 2 ab + b² ( a + b ) ( a – b ) = a² -
b² ( a + b ) 3 = a 3
+ 3 a2b + 3 a b 2
+ b 3 ( a - b ) 3 = a 3 - 3 a2b + 3 a b 2 - b 3 ( a² - 2
ab + b² ) ( a + b) = a 3 +
b 3 ( a² + 2 ab + b² ) ( a
- b) =
a 3 - b 3 |
|
|||||||||||||||||
|
|
D’une
manière très générale , le développement de «
( a + b ) n est « homogène » en « a » et « b » , ce
qui veut dire que la somme des exposants des lettres est la même dans chaque
terme. Quant aux
coefficients numériques, ils sont donnés par le triangle de Pascal. Dans lequel chaque terme est la
somme des deux termes situés au-dessus
et au-dessus à gauche. ( Exemple : 15 =
10 + 5 ) |
|
||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
2 |
1 |
|
|
|
Pour : ( a + b ) ² |
|
||||||||||||
|
|
1 |
3 |
3 |
1 |
|
|
Pour : ( a + b ) 3 |
|
|
|||||||||||
|
|
1 |
4 |
6 |
4 |
1 |
|
|
|
|
|
|
|
||||||||
|
|
1 |
5 |
10 |
10 |
5 |
1 |
|
|
|
|
|
|
||||||||
|
|
1 |
6 |
15 |
20 |
15 |
6 |
1 |
Pour ( a + b ) 6 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Exemple : ( a + b ) 6 = a
6 + 6 a 5 b + 15
a 4 b2 + 20 a 3 b 3 + 15 a 2
b 4 + 6 a b 5 + b 6 |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
· 1 – 7 : Différence de deux carrés. |
|
||||||||||||||||||
|
|
( d’après le chapitre précédent ) a²
- b²
= ( a + b ) ( a – b ) Cette formule très importante est l’une des clés
du calcul algébrique. Elle s’applique quels que soient « a » et
« b ». Voir quelques exemples ci-dessous : Série a ) : · x ² - 4 = ( x + 2) ( x –
2) · 16 x ² - 81 = ( 4 x + 9 ) ( 4 x – 9 ) · · ( 2 x + 3 ) ² - 49 = ( 2 x + 3
+ 7 ) ( 2 x + 3 – 7 ) = ( 2 x + 10 ) ( 2 x – 4 ) · ( 3 x – 5 ) ² - ( x + 4 ) ²
= [ ( 3 x – 5 ) + ( x + 4 ) ] [( 3 x –
5 ) - ( x + 4 ) ]
= ( 3 x – 5 +
x + 4 ) ( 3 x – 5 - x - 4 )
= ( 4 x – 1 ) ( 2 x – 9 ) |
|
||||||||||||||||||
|
|
Série b ) :Parfois
cette identité exige que l’on se rappelle que : « Tout nombre positif est le carré de sa racine carrée » |
|
||||||||||||||||||
|
|
· 11 = · 17 = · x² - 13 = ( x + · ( 7 x – 4 )
² - 21 = ( 7 x – 4 + |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
1 – 8 La mise en facteur commun. |
|
|||||||||||||||||||
|
|
C’est l’opération inverse du développement par
application de la propriété distributive. «
a n + b n – c n = n
( a + b – c) » Pour
effectuer une mise en facteur commun il faut : 1°) Apercevoir la lettre ,
le nombre ou le groupe de lettres qui figures comme « facteurs »
dans tous les termes , sans exception
. 2°) Ecrire le facteur commun. 3°) Ouvrir une parenthèse. 4°) Ecrire , dans la
parenthèse , tout ce qui reste , y
compris les signes , après suppression , dans chaque terme, du facteur
commun : Tout ce qui reste ,
ce sont les quotients de chaque terme par le facteur commun. 5°) Fermé la parenthèse. Il est à noter que le contenu de la parenthèse
est l’ensemble des quotients de chaque terme, par le facteur commun. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exemples : |
|
||||||||||||||||||
|
|
1°) E = 3 x
6 - 8 x 5 + Le facteur commun est « x² » et l’on
écrira : E = 2°) E = x 8 y 6 + x 6 y 8 Le facteur commun est évidemment : x 6 y 6
E = x 6 y 6 ( x ² + y ² ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
1-9 Mise en
facteur commun « forcée ». |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Il arrive que l’on ait besoin ,
dans une somme de termes, de mettre en facteur commun une quantité qui , pourtant,
n’est pas facteur dans chacun des termes . Mais ,
d’après la phrase qui suit , on écrit dans la parenthèse les quotients des
différents termes par la quantité mise en facteur commun. |
|
||||||||||||||||||
|
|
Voir les exemples qui suit ,
ce procédé est souvent utilisé….. 1°) E
= 2°) E = a x 3 + b x² + c x = 3°) E = a x²
+ b x + c = |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
2 )
La décomposition en produit de facteurs
et son rôle essentiel . LA FACTORISATION. |
|
|||||||||||||||||||
|
|
Les produits de facteurs interviennent dans la
plupart des questions (ou problèmes) d’algèbre : -
Simplification de
fractions ; -
Réduction au même
dénominateur ; -
Résoudre des
équations ; -
Résoudre des
inéquations ;…….. On ne peut
se passer d’eux. Apprendre à décomposer une expression en produit de facteurs
est de toute nécessité et de toute urgence….. Or, il n’existe pas de procédé général permettant
d’effectuer une telle décomposition . Cependant en
algèbre élémentaire, on doit toujours penser à utiliser : -
la mise en facteur commun , partielle ou totale. -
Les différences de
deux carrés : « a² -
b² = ( a + b ) ( a – b )» qui jointes aux identités
( chapitre 1-6) conduisent avec un peu de perspicacité et beaucoup
de « métier » (expériences),
au résultat désiré. |
|
||||||||||||||||||
|
|
Donc voici ci-dessous une séries d’exercices
progressifs ( s’imprégner) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
2-1 Intervention de la mise en
facteur commun seule. |
|
||||||||||||||||||
|
|
Exercice 1 : E
= ( 2 x + 5 ) ( 3 x – 4 ) - 2 ( 2 x + 5 ) ( x – 1 ) + ( 2 x + 5 ) |
|
||||||||||||||||||
|
|
Solution : Le facteur commun est
en évidence « ( 2 x + 5 ) » |
|
||||||||||||||||||
|
|
E
= ( 2 x + 5 ) [ ( 3 x – 4 )
- 2 ( x - 1 ) + 1 ]
E
= ( 2
x + 5 ) ( 3 x – 4 - 2 x + 1
+ 1 ) E =
( 2 x + 5 ) ( x – 1 ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 2 : E =
( 4 – 5 x ) ( 3 x + 2 ) + 3 ( 4 – 5 x ) x – (
4 – 5 x ) Réponse : -
Facteur
commun : ( 4 – 5 x ) -
E = ( 4 – 5 x ) ( 6 x + 1 ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 3 : E =
( 7x + 3 ) ( 5 x -1 ) - 3 ( 7x +4
) + 2 ( 7 x +4 ) ( x – 3 ) Réponse : E
= ( 7 x +4 ) ( 7 x – 10 ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
2 – 2 Souvent le facteur commun n’est pas en
évidence et n’apparaît que grâce à une transformation d’écriture , : telle
que : « a
– b =
- ( b – a ) » |
|
||||||||||||||||||
|
|
Exercice 4 . E = ( 2x
– 7 ) ( 3x + 4 ) – 2 x + 7 + 2 ( 2 x – 7 ) ( x + 1 ) Ici il faut d’abord remarquer que : - 2 x + 7 = -
( 2 x – 7 ) Et écrire : E = ( 2x – 7 ) ( 3x + 4 ) – ( 2 x -
7) + 2 ( 2 x – 7 ) ( x + 1 ) Le facteur commun est
alors : « ( 2 x – 7 ) » E
= ( 2 x – 7 ) [( 3x + 4 ) - 1 + 2 ( x + 1 ) ] E
= ( 2
x – 7 ) [ 3x + 4 - 1 + 2
x + 2 ) ] E
= ( 2
x – 7 ) ( 5 x + 5 ) E
= 5 ( 2
x – 7 ) ( x + 1 ) |
|
||||||||||||||||||
|
|
Exercice 5 . E = ( 4
– 3 x ) ( x + 2 ) – 4 + 3 x Ecrire : E = ( 4 – 3
x ) ( x + 2 ) – ( 4
- 3 x ) E
= 4 – 3 x ) [ ( x + 2 ) – 1 ] E
= 4 – 3 x )
( x + 1 ) |
|
||||||||||||||||||
|
|
Exercice 6 . E = ( 7 x – 3
) ( 8 x + 1 ) +
( 7 x – 3 ) x
- 7 x + 3 Réponse : E = 9 ( 7 x – 3
) x |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
2 – 3 Parfois pour apparaître , le facteur commun
exige une mise en facteur partielle dans certains termes. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 7 . E = ( 7 – 2 x
) ( x + 5 ) – ( 21 – 6 x ) ( 2 x – 1 ) |
|
||||||||||||||||||
|
|
Aucun facteur commun n’apparaît
d’emblée. Mais ( 21
– 6 x ) = 3 ( 7 - 2 x ) et l’on a : E = ( 7
– 2 x ) ( x + 5 ) – 3 ( 7
- 2 x ) ( 2 x – 1 ) le facteur commun est alors : ( 7 - 2 x ) E = ( 7
– 2 x ) [ ( x + 5 ) – 3 ( 2 x – 1 )] E = ( 7
– 2 x ) ( x + 5
– 6 x +3 ) E = ( 7
– 2 x ) (
8 – 5 x ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 8 . E = ( 3
x + 4 ) ( 7 x – 1 ) + ( 12 x + 16 ) (
x + 2 ) |
|
||||||||||||||||||
|
|
Voir que : ( 12 x + 16 ) =
4 ( 3 x + 4 ) E =
( 3 x + 4 ) ( 11 x + 7 ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 9 . E = ( 2 x + 3 ) ( 5 x – 1
) - 3 ( x + 2 ) ( 25 x – 5 ) Réponse : Voir : (25 x – 5 ) = 5 ( 5 x – 1 ) E =
( 5 x – 1 ) [
( 2 x + 3 ) - 15 ( x + 2 ) ] E
= ( 5 x – 1 ) ( - 13 x – 27
) =
- ( 5 x – 1 )( 13 x + 27 ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Dans le même ordre d’idée ,
nous allons voir des exercices un peu plus compliqués. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 10 . E = x ² + a x + b x + a b |
|
||||||||||||||||||
|
|
Remarquer que : x ² + a x = x ( x + a )
; b x + a b = b
( x + a ) Alors : E =
x ( x + a ) + b ( x + a ) ;
E = ( x + a ) ( x + b ) |
|
||||||||||||||||||
|
|
Exercice 11 . E = x 3 – x ² + x - 1
Ecrire : x 3 – x ² = x
² ( x – 1 ) Réponse : E
= ( x
– 1 ) ( x ² + 1 ) |
|
||||||||||||||||||
|
|
Exercice 12 . E = x ² + x y + y + x |
|
||||||||||||||||||
|
|
Réponse : E = (
x + 1 ) ( x + y ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
2 – 4 : Intervention
des différences de deux carrés seules . |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 13 . E = ( 3 x – 2 ) ² - ( 2 x + 1 ) ² |
|
||||||||||||||||||
|
|
On a immédiatement : E =
[( 3 x – 2 ) + ( 2 x + 1 ) ]
[( 3 x – 2 ) - ( 2 x + 1 ) ] E =
( 3 x
– 2 + 2 x + 1 ) ( 3 x – 2
- 2 x - 1 ) E =
( 5 x
– 1 ) ( x – 3 ) |
|
||||||||||||||||||
|
|
Exercice 14 . E = ( 5 x + 3 ) ² - (
13 x – 2 ) ² |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Ecrire : E =
[ ( 5 x + 3 ) +
( 13 x – 2
)] [( 5 x + 3 ) -
( 13
x – 2 )] Réponse : E =
( 18 x + 1 ) ( 5 – 8 x ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 15 . E = ( 15 x + 2 ) ² - (
3 x – 4 ) ² |
|
||||||||||||||||||
|
|
Réponse : E = 12 ( 9 x – 1 ) ( 2 x + 1 ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
2 – 5 : souvent la différence de
deux carrés ne sont pas en évidence et
il y a lieu de les faire apparaître ,
notamment par application des identités fondamentales du chapitre 1-6 |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 16 . E = 9 x ² + 6 x y + y ² - 25 (
x ² - 2 x y + y ² ) |
|
||||||||||||||||||
|
|
Il y a lieu de remarquer d’abord que : |
|
||||||||||||||||||
|
|
|
9 x ² + 6 x y + y ² = ( 3 x + y ) ² x ² - 2 x y + y ² = ( x - y ) ² |
|
|||||||||||||||||
|
|
On peut écrire : E =
( 3 x + y ) ² - 25 ( x - y ) ² On a alors une différence de deux
carrés. |
|
||||||||||||||||||
|
|
E
= [ ( 3 x + y ) + 5 ( x - y )]
[ ( 3 x + y ) - 5 ( x - y )] E
= ( 3 x + y + 5 x
- 5 y ) ( 3 x + y -
5 x + 5 y ) E
= ( 8
x - 4 y ) ( - 2 x + 6 y ) E
= 4 ( 2 x - y
) 2 ( - x + 3 y ) = 8 ( 2 x
- y ) ( 3 y - x ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 17 . E = 3 x² + 6 x + 3 – 12 y ² +
36 y – 27 |
|
||||||||||||||||||
|
|
Remarquons que : 3 x² + 6 x + 3 = 3 (
x² + 2 x + 1 ) = 3 ( x + 1 ) ² |
|
||||||||||||||||||
|
|
|
3 x² + 6 x + 3 = 3 ( x² + 2 x + 1 ) =
3 ( x + 1 ) ² – 12 y ² + 36 y – 27 = -
3 ( 4 y ² + 12 y – 9 ) = - 3 ( 2 y – 3 ) ² |
|
|||||||||||||||||
|
|
E = 3
[ ( x + 1 ) ²
- ( 2 y – 3 ) ² ] Réponse : E = 3 ( x + 2 y – 2 ) ( x – 2y + 4 )
|
|
||||||||||||||||||
|
|
Exercice 18 . E = 3 x ² - y ² - 2 y z – z ² |
|
||||||||||||||||||
|
|
Réponse : E = ( x + y + z ) ( x - y
- z ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 19 . E = 4 a ² b ² - ( a
² + b ² - c ² )² |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Il y a
d’abord une différence de deux carrés : E = [ 2 a b + a² + b
² - c ² ]
[ 2 a b - a² -
b ² + c ² ] Il faut alors procéder à des regroupements de
termes. : |
|
||||||||||||||||||
|
|
|
a² + b² + 2 ab = ( a + b
) ² - a²
- b² + 2 ab = - (
a ² + b ² - 2 a b ) = - ( a – b ) ² |
|
|||||||||||||||||
|
|
Dés lors : E = [( a + b ) ² - c ² ]
[ c² - ( a + b ) ² ] Et il n’y a plus , dans
chaque crochet, qu’à effectuer les différences de deux carrés : E = ( a
+ b + c ) ( a + b - c ) ( c + a – b ) ( c – a + b ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 20 . E = a ² - b ² + x ² - y ² + 2 ( a x – b y ) |
|
||||||||||||||||||
|
|
Ecrire : E = x ² + 2 a x + a ² - ( y ² + 2 b
y + b ² ) |
|
||||||||||||||||||
|
|
Réponse :
E = ( x + y + a + b ) ( x – y + a – b ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 21 . E = a ² - b ² - c ² + d ² - 2 ( a d
– b c ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Réponse : E = ( a – d + b – c ) ( a – d – b +
c ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
2 – 6 Intervention des
différences de deux carrés , combinées avec la mise
en facteur commun. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 22 . E = ( 3 x – 5 ) (
2 x – 7 )+ 4 ( 1 – 3x ) ( 3 x – 5 ) – 9 x ² + 25 |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Aucun facteur commun n’est en évidence ; mais : – 9 x ² + 25 = – ( 9 x ² - 25 )
= - ( 3 x + 5 ) ( 3x – 5 ) donc : E = ( 3 x – 5 ) ( 2 x
– 7 )+ 4 ( 1 – 3x ) ( 3 x – 5 ) - ( 3 x + 5 ) ( 3x – 5 ) Cette fois « ( 3 x – 5 ) » est
en évidence dans tous les termes. E = ( 3 x – 5 ) [( 2 x – 7
)+ 4 ( 1 – 3x ) - ( 3 x + 5 ) ] Ou : E = ( 3
x – 5 ) ( 2 x – 7 + 4 – 12 x) - 3 x -
5 ) E = ( 3
x – 5 ) (13 x + 8 ) |
|
||||||||||||||||||
|
|
Exercice 23 . E = ( 4 x – 1 ) (
x + 3 ) – 3 ( 16 x² - 1 ) – ( 4 x – 1 ) ² |
|
||||||||||||||||||
|
|
Voir que : ( 16 x² - 1 ) = (
4 x + 1 ) ( 4 x – 1 ) |
|
||||||||||||||||||
|
|
Nous mettons « ( 4 x – 1 ) » en
facteur commun |
|
||||||||||||||||||
|
|
Réponse : E = ( 4 x – 1 ) ( 1 – 15 x ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 24 . E = (
x² – y ² )
( 2 x + y ) + ( x + 3 y ) ( 4
x² - y ² ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Réponse :
E = ( x + 3 y ) ( 2 x + y ) ( 3 x – 4 y ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
2 – 7 Voir les exercices « exemples »
suivant dans lesquels la plupart des considérations précédentes
interviennent utilement. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 25 . E = (
x + y ) ( x
- z ² ) + ( x – z ) ( x² - y ²
) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Il suffit d’écrire :
E = (
x - y ) (
x + z ) ( x – z ) + ( x – z ) ( x + y ) ( x – y ) et mettre « ( x – y ) ( x – z ) en facteurs
communs.. E =( x – y ) (
x – z ) ( x + z + x + y ) Réponse finale : E =( x – y ) ( x
– z ) (2 x + z + y ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 26 . E = ( x – 1 ) ( x – 2 ) ( x – 3 ) + ( x – 1 ) ( x – 2 ) – x + 1 |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
On voit une mise en facteur commun
partielle dans les deux premiers termes : E = ( x – 1 ) ( x – 2 ) ( x
– 3 + 1 ) – ( x – 1 ) E = ( x – 1 )
( x – 2 )² - ( x – 1 ) Mettre ( x – 1 ) en facteur !!! dans l’ensemble et décomposer la
différence de deux carrés. Résultat final : E = ( x – 1 )
² ( x – 3 ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Exercice 27 . E = x 3 - 2 x² - 3 x |
|
||||||||||||||||||
|
|
On va faire des mises en facteur commun
partielles : E
= x ( x² - 1 ) – 2 x ( x + 1 ) Réponse : E = x (
x + 1) ( x – 3 ) |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
Voir
les Travaux auto formatifs
. A apprendre et
retenir !!!!!!!!!!!!!