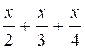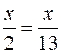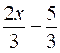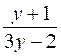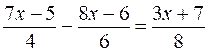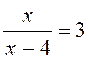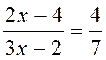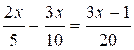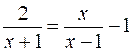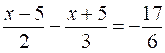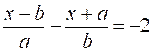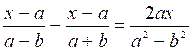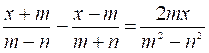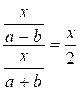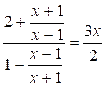Expression algébrique cours N° 3

Pré requis:

Expression et somme algébrique (calcul numérique) niveau 1

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent :

Voir les expressions algébriques :

Objectif suivant

2°) Suite.

Liste 303

DOSSIER : N°4 : ALGEBRE (Généralités) Les "EQUATIONS" et "INEQUATIONS " du premier degré .


I ) l’ EGALITE	Définition et résolution.
II ) les EQUATIONS:	Définition et résolution.
III ) LES INEGALITES:	Définition et résolution.
IV ) L’ INEQUATION	Définition et résolution.

TEST

COURS

Devoir Contrôle

Devoir niveau I évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS.

Vocabulaire : déjà vu:
« Binôme » :
« Expressions algébriques équivalentes. »
« Expression algébrique rationnelle: »
« Expression algébrique irrationnelle: »
« Expression algébrique rationnelle entière : »
« Expression algébrique rationnelle fractionnaire : »
« Identité »
« Monôme : »
« Polynôme : »
« Termes semblables: »
« Trinôme : »
« Polynôme entier ou rationnel : »
« Valeur numérique d'un terme : »
« Valeur numérique d'un polynôme : »
« Calcul algébrique. »

Info plus !!!!

I ) LES EGALITES :

IDENTITE :

L'expression de l' égalité de deux expressions équivalentes constitue une identité .

Pour la distinguer d'une égalité algébrique on emploie quelque fois le signe º qui veut dire "identique à …."

Exemple : ( a + b ) ² º a² + 2ab + b²

On appelle identité une égalité évidente (ou une égalité satisfaite) quelles que soient les valeurs numériques des lettres qui y entrent

Ainsi : 3 8 = 46 est une identité

8 = 8 est une identité

(a - b )² = a² - 2ab + b² est une identité.

Mais , considérons l'égalité 5 x = 40

Ce n'est pas une identité , car si je remplace "x" par 3 , par exemple , le membre de gauche est égal à 5 3 ou 15 , le membre de droite est égal à 40 et 15 n'est pas égal à 40. Si je remplace "x" par 8 , le membre de gauche est égal à 40 , et par conséquent l'égalité se transforme en identité : 40 = 40

L'égalité 5x = 40 ne se "réduit donc à une identité" que si on remplace par une valeur convenablement choisie , c'est une équation.

Vers "Identités remarquables"

II ) EQUATIONS:

On appelle " équation" une égalité qui ne se réduit à une identité que pour des valeurs particulières des lettres qui y entrent.

Une équation est donc une égalité qui renferme au moins une inconnue et qui ne peut être vérifié que lorsque certaines valeurs numériques , qu'il s'agit de trouver ,sont mises à la place des inconnues.

Inconnues:

Les lettres qu'il faut remplacer par des valeurs particulières pour obtenir une identité sont les inconnues de l'équation ; on les désigne généralement par les lettres "x" , "y" , "z" , "t" , "u"

Solutions ou racines de l'équation :

Les valeurs particulières qu'il faut donner aux inconnues pour avoir une identité sont les "solutions" ou "racines" de l'équation.

Dans la résolution d’une équation du second degré les racines sont les valeurs de « x » pour la valeur de « y=0 » (voir le tracé d’une équation du second)

Equation est satisfaite ou vérifiée

On dit qu'une équation est satisfaite ou vérifiée pour les valeurs des inconnues qui sont les racines .

Résolution des équations :

Résoudre une équation, c'est trouver les valeurs particulières qui , mises à la place des inconnues , donnent une égalité évidente .(on dit aussi "égalité vraies")

On dit aussi : Résoudre une équation c'est rechercher et trouver ses racines .

Une équation peut contenir une ou plusieurs inconnues.

Equation entière:

Une équation est dite "entière" quand elle ne contient aucune inconnue en dénominateur.

Equation rationnelle :

Une équation est dite "rationnelle" quand elle ne contient aucune inconnue sous un radical.

Equation irrationnelle :

Une équation est dite "irrationnelle" quand elle contient un radical. Exemples : ; ;

Degré d'une équation :

On appelle "degré d'une équation" entière ou rationnelle la somme des exposants des inconnues dans le terme où cette somme est la plus grande .

Exemples :

L'équation 2x -8 = x +14 est du premier degré.

L'équation 5 x² - 8x = 0 est du 2^ème degré

L'équation xy +x -y + 1 = 0 est du deuxième degré en "x" et "y" ( la somme des exposants dans le terme "xy" est 2 ).

Les principales équations sont:

	Forme de l'équation :
Du premier degré à une inconnue	ax = b
Du premier degré à deux inconnues	y = ax , y = ax +b
Du second degré à une inconnue	ax²= b
Du second degré à deux inconnues	y = ax²; y = ax²+ b

A titre d’information : l’équation 2x³ -8 = x² +14 est du troisième degré , il en est de même de l’équation . x² y + 1 = 0

III ) LES INEGALITES: ( info ++)

Définitions :

1° ) Un nombre algébrique "a" est plus grand qu'un autre nombre algébrique "b" , lorsque la différence : ( a- b ) est positive

Voir différence de deux nombres algébriques (de décimaux relatifs )

Exemple: soient les nombres : "a" = (+3 ) et "b" = (-4)

La différence de ces deux nombres est (+3) - (-5) = (+8)

On écrira que le nombre (+3) est plus grand que le nombre (-4)

Ce qui se traduit par l'écriture : (+3) > (-4) on a ainsi "une inégalité"

2°) Un nombre algébrique "a" est plus petit qu'un autre nombre algébrique "b" , lorsque la différence ( a- b ) est négative

Exemple : soient les nombres "a" = (-11) et "b" = (-5)

La différence de ces deux nombres est: (-11) - ( -5 ) = (- 11 ) + ( + 5 ) = ( - 6 )

On écrira que le nombre ( -11 ) est plus petit que le nombre ( -5)

Ce qui se traduit par l'écriture : (- 11 ) < (- 5 ) ; on a ainsi "une inégalité"

Les principes ( ou théorèmes ) applicables aux équations sont applicables aux inégalités .

Théorème 1 et 2 :

On peut ajouter ou retrancher un même nombre algébrique aux deux membres d'une inégalité , sans changer cette inégalité.

Exemple : soit l'inégalité : (+4) > (-3)

Ajoutons le nombre algébrique ( -3 ) aux deux membres , on a :

(+4) + ( - 3 ) > (-3) + ( - 3 )

ainsi : (+1) > (-6) , ce qui est encore vrai.

On démontrerait de même ce principe , si on diminuait d'une même quantité les deux membres d'une égalité.

Théorème 3 et 4:

Si on multiplie les deux termes d'une inégalité , ou si l'on divise ces deux termes par un même nombre , on obtient encore une inégalité.

Attention : cette inégalité ne changera pas de sens , si on a multiplié ou si l'on a divisé par un nombre positif . mais cette inégalité changera de sens , si on a multiplié ou divisé par un nombre négatif.

Exemple : soit l'égalité (+7 ) > (-5)

Multiplions les deux termes par (+4) , on a , d'après la règle des signes :

(+7 ) (+4) > (-5) (+4)

ou (+ 28 ) > ( -20 ) ce qui est vrai.

Multiplions les deux termes de la même inégalité par (-3) on a , d' après la règle des signes : (+7 ) > (-5)

a) (+7 ) ( -3 ) donne ( -21 )

b ) (- 5 ) ( -3 ) donne ( + 15 )

On ne peut pas écrire que ( -21 ) > (+15 ) , il faut obligatoirement changer le sens du signe > et écrire que ( -21 ) < (+15 )

ou si (+7 ) > (-5) ; changer le sens du signe de l'inégalité si l'on multiplie par un nombre négatif : (+7 ) ( -3 ) < (-5) ( -3 )

On démontrerait que ce principe est applicable si l'on divisait les deux termes d'une inégalité par un nombre positif ou un nombre négatif.

IV ) L’ INEQUATION ( info +)

Une "inéquation" est une inégalité dans laquelle entre une quantité inconnue.

Exemple 1: On veut résoudre l'inéquation : 2x - 3 > 3 x -20

C'est à dire trouver pour quelles valeurs de "x" l'inéquation est vérifiée .

Pour cela , on applique à la résolution de l'inéquation toutes les règles qu'on applique à la résolution d'une équation. On aura donc:

2x - 3 > 3 x -20

20 - 3 > 3 x -2x

1 7 > x

Ou x < 17

En conclusion :Pour que l'inéquation soit vraie , il faut qu'on donne à "x" des valeurs plus petite que 17

Exemple 2 : Résoudre l'inéquation , c'est à dire trouver les valeurs qui satisfont à l' inéquation suivante :

8x -5 >

nous chassons le dénominateur , on a :

2 ( 8 x -5 ) > 15x -8

16 x - 10 > 15x -8

16x - 15x > 10 -8

x > 2

Conclusion : toutes les valeurs positives , à partir de (+2) jusqu'à (+ l'infini ) sont les valeurs qui satisfont à l'inéquation donnée.

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°) Donnez la définition d’une expression algébrique.

2° )Donner la définition de « variable »

3° )Donner la définition de « somme algébrique ».

4° )Quelle relation y a t - il entre « somme algébrique » et « expression algébrique »?

5° )Pour faire du calcul algébrique ,que doit-on faire de l’expression algébrique ?

6°) Donner la procédure permettant de transformer une expression algébrique en somme algébrique.

EVALUATION: NIVEAU I

Résoudre les équations suivantes:

Série 1
x - 2 = 5
x - 4 = 5 - 2 x
Série 2
5 x - 18 = 3 x
3 + 2x = 1 - x
Série 3
12x - 8 = 172
5x -4 = x - 28

Série 4
3x +4 = 9 -4x
5x -18 =-3x +6
Série 5
4x +3 +5 = 3x +12
5x -13 = 2x -4
Série 6
6x + 160 = 40 + 8x
2x -1 = 3x +2
Série 7
3x -4 -2 ( x - 5) = 18
=45
Série 8
= 11 –x
6+ +17
Série 9
- 8 =
+20= x +25
Série 10
+ 5 = 2 +x
- 5 = 3y - 85
Série 11
( y -2 ) 7 =
=
Série 12
= 1 -
5 ( y +3) = (y -3)
Série 13
= 7
+ 7 = + 9
Série 14
=50
= 5 x -46
Série 15
= x +3
2= x -2
Série 16

(x-7) = (x-2)
Série 17


Série 18


Série 19