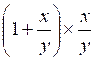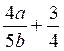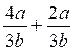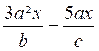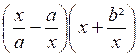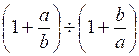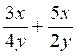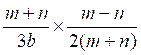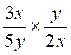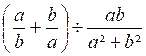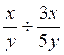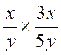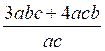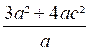|
|
|
DOC : Formation
Individualisée |
DOC : Elève. |
|
Résumé d’une progression : ALGEBRE. N° 24 |
Information « TRAVAUX » ;Cliquer sur le mot !. |
|
OBJECTIFS :- médiation en algèbre. |
I ) Pré requis:
|
i9 |
:i |
II ) ENVIRONNEMENT du dossier :
|
1°) Calcul
numérique (réduire
au même dénominateur) 2°) Progression
d’algèbre) Dossier précédent 23: |
Info ++ |
COURS sur : Résumé
sur les FRACTIONS ALGEBRIQUES.
IV)
INFORMATIONS « formation
leçon » :
|
|
Travaux auto -
formation. (dans le cours) |
|
Corrigé des travaux
auto - formation. |
|||
|
|
||||||
|
Leçon |
Titre |
|
N°24 |
FRACTIONS ALGEBRIQUES. |
Déjà
vu : voir cas par cas.
4
I°) Réduction au même dénominateur.
1° exemple : recherche d’un dénominateur commun
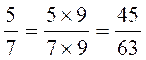 et
et 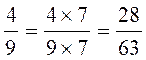
Pour réduire deux fractions au même dénominateur on
multiplie les deux termes de chaque fraction par le dénominateur des autres.
2° exemple : On peut parfois prendre le plus grand
dénominateur comme dénominateur commun.
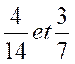
Nous prenons 14 pour
dénominateur commun, on a 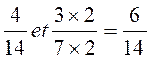
3° exemple : On cherche un dénominateur commun
un multiple proche du plus grand dénominateur : 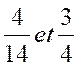
Nous prenons 2 fois 14, ou 28, comme dénominateur commun ; on a :
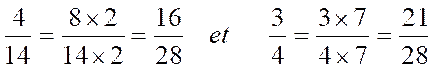
II) Somme et différence de fractions. (info Complémentaires
« addition » et info. « soustraction »
Pour additionner ou soustraire deux
fractions on les réduit au même
dénominateur, puis on ajoute ou on soustrait le second numérateur au premier
numérateur en conservant le dénominateur commun.
Exemples :
1°
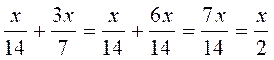
2°) 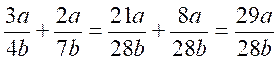
3°) 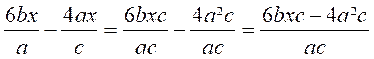
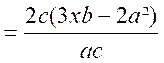
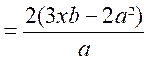
III) Produit de
fractions. ( info complémentaires)
Pour calculer le produit de
fractions on multiplie les numérateurs entre
eux et les dénominateurs entre eux.
Exemples :
1°
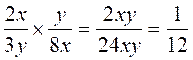
2° 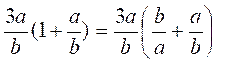
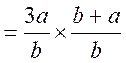
![]()
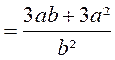
IV) Quotient de fractions. ( Info complémentaires)
Pour calculer le quotient de deux
fractions on multiplie la fraction dividende par la fraction diviseur renversée
Exemples :
1°) 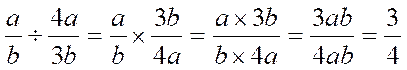
2°)
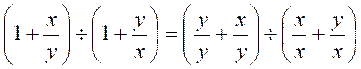
![]()
|
Titre |
|
|
N°24 |
TRAVAUX d’Auto - FORMATION sur FRACTIONS ALGEBRIQUES. |
1°)
Pour réduire deux fractions au même
dénominateur on.
.
……………………………………………………….........................................
2°)
Pour additionner ou soustraire deux fractions
on ………………………………………………………………………………………..
3°)
Pour calculer le produit de fractions on
………………………………………………………………………………………..
4°)
Pour calculer le quotient de deux fractions on
………………………………………………………………………………………..
I°) Réduire au même dénominateur.
1°) 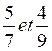
.2°) 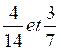
3°) 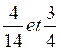
II) Calculer les sommes et la différence de fractions.
1° 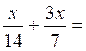
2°)
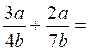
3°) 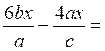
III)
Calculer le produit de fractions
1°) 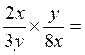
2° ) 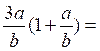
IV) calculer le quotient de deux fractions
1°) 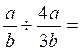
2°)
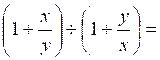
2°) Série
« effectuer » :
|
1 |
|
|
A |
|
|
2 |
|
B |
|
|
|
3 |
|
C |
|
|
|
4 |
|
D |
|
|
|
5 |
|
E |
|
|
|
6 |
|
F |
|
1°) 4 créanciers ont à se partager 68 000
euros. La créance du premier n’est que la moitié du second. Celle du second les
4/5 de celle du troisième. Celle du troisième les 5/6 de celle du quatrième.
Combien revient-il à chaque créancier ?
CORRIGE :
1°) diviser :
|
1 |
2a² b c ¸a |
|
A |
2a²b c ¸
b |
|
2 |
2a²b c ¸
a b |
|
B |
2a²b c ¸
a b c |
|
3 |
|
|
C |
|
|
4 |
|
|
D |
|
|
5 |
|
|
E |
|
Problème :
1°)
Une personne a placé à intérêt simple , au taux
de 3%, un certain capital et,au taux de 4% un autre
capital. Le second est les 8/11 du premier. Les deux capitaux et intérêts réunis se sont élevés au
bout de 3 ans à 20950 euros. Quels étaient les deux capitaux placés ?