|
|
||||
|
Ici : Devoir auto_ formatif. |
Ici : Devoir formatif |
|||
|
|
|
|||
|
|
||||
|
|
|
|
||
|
|
Devoir : Partie
I : RAPPORTS et RAPPORTS EGAUX |
|
||
|
|
|
|
||
Ce cours est en trois partie
et il prépare celui sur la fonction linéaire.
CONTROLE :
1- On appelle « rapport »
la division d’un nombre par un autre nombre.
Le modèle mathématique d’un « rapport » est « une
fraction ».
2- Traduction en langage
mathématique : 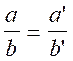
3- On appelle « rapports
égaux » des divisions de deux
nombres qui ont le même quotient et dont le reste des divisions est
nul .
(on dit aussi :quotient exact )
4- Le modèle mathématique de deux rapports égaux est l’égalité de deux fractions
5- Le modèle mathématique de plusieurs rapports égaux est l’égalité de plusieurs fractions
. 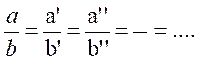
6_ Lorsque l’on calcule le
quotient de chaque rapport on obtient un rationnel (nombre) identique , c’e
nombre dit « constant » est
appelé « k ».
7- Traduction en langage mathématique : 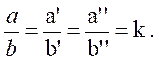
8- Avec une suite de rapports égaux ,on forme un
autre rapport(ou fraction) égal à chacun d’eux
( de chaque rapport) qui
aura pour numérateur la somme des
numérateurs et pour dénominateur la somme des dénominateurs .
9- Traduction en langage mathématique : si; alors on a 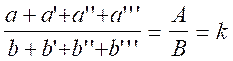
10 - Pour vérifier si une suite de rapports forme une suite de rapports égaux ,on fait la somme des numérateurs sur la somme des
dénominateurs et l'on effectue la
division; on compare avec le résultat d'une division d'une fraction choisie au
hasard.
![]() =
= ![]() =
=
![]() =
=
![]() ; alors on a
; alors on a
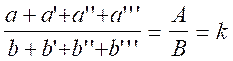
12 - Vérifier si deux suites de
nombres forment une suite de rapports égaux.
Méthode :
Dans une suite de fractions
on considère les numérateurs comme formant une première suite de nombres
et on considère les dénominateurs
forment une deuxième suite de nombres.
On calcule la somme des numérateurs , puis la
somme des dénominateurs , ensuite on calcule le quotient des deux sommes
obtenues.
On calcule le quotient d’une fraction dans la suite de départ ,Si
les deux quotients sont identiques on
dira que : les deux suites
(numérateurs et dénominateurs) forment une suite de rapports égaux.
Application :
13- On représente une suite de
nombre « S1 » de la façon suivante : « S1 » = { 2 ; 3 ;4 }
14 - On
représente deux suites de nombres de la façon suivante :
«
S1 » = { 2 ; 3 ;4 } ;
« S2 » = { 4 ; 6 ; 9 } ; on
donne des valeurs « au hasard ».
15- Méthode : pour former
deux suites de nombres qui formera une suite de rapports égaux on créera une première suite de nombres , ensuite on
créera une deuxième suite de nombres en
multipliant les nombres de la première suite par un même nombre multiplicateur
.
Exemple :
on crée« S1 » = { 2 ; 3 ;4 }
; je multiplie par « 2 »
tous les nombres de la première suite pour obtenir la suite 2 « S2 »
= { 4 ; 6 ;8 }
Ensuite je forme la suite de rapports
égaux S ={ ![]() ;
;
![]() ;
;
![]() }
}
1°) Les deux suites [
9 ;11 ;19 ;25 ;31 ;]
et [27 ;
33 ;57 ;75 ;93 ;] sont - elles des suites de nombres
proportionnelles ?
|
9 |
11 |
19 |
25 |
31 |
|
|
27 |
33 |
57 |
75 |
93 |
|
|
|
|
|
|
|
|
1) somme des numérateurs : 9+11+19+25+31= 95
2 ) somme des dénominateurs = 27+33+57+75+93= 285
3 ) division des deux sommes 285:95 =3
4 ) division d'un rapport : 27:9 = 3
5 ) on compare les deux résultats : 3 et 3 ; les quotients sont égaux
6 )
Conclusion : la suite de rapports est une suite de rapports égaux
A) Si
l’on paye dans un restaurant 2400 €
pour un mois (30 jours)de pension
,que paiera-t-on pour :
5jours ; 12jours ; 21 jours
|
2400
€ |
X1 |
X2 |
X3 |
|
|
30 |
5 |
12 |
21 |
|
2400 :30 = X1 :5 ; X1 = 2400 fois 5 : 30 = 400 €
X2= 960 € X3
= 1680 €