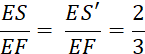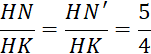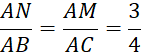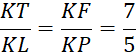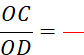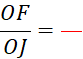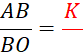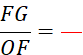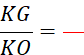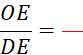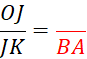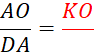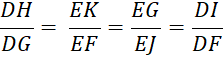|
DOC : Formation Individualisée |
DOC : Elève. |
|
DOSSIER N° GEOMETRIE PLANE (partie
2) |
Information « TRAVAUX » |
|
OBJECTIFS : - Savoir ……………………… |
I ) Pré requis:
|
i9 |
THALES Pré requis |
:i |
|
i9 |
:i |
II ) ENVIRONNEMENT du dossier :
|
Dossier suivant : Démonstration
« Thalès » : |
2.
Liste des cours de géométrie plane.. |
||
|
|
|
|
3.
|
Module « THALES »
GEOMETRIE PLANE: LES
PROPRIETES DE THALES. ( au collège)
Chapitres :
|
i9 |
1°) Les parallèles équidistantes. Rappel : Projection du milieu d’un segment. ; Projection d’une graduation régulière. ;
Théorème : parallèles équidistantes. |
:i |
|
i9 |
2) Partage d’un segment. |
:i |
|
|
3°) Construction de points « M » et
« N » d’un triangle « ABC » tels que : |
|
|
|
4°) Expérimentation sur des triangles quelconques . |
|
|
|
5°) Théorème de Thalès. |
|
|
|
6 °)
Quatrième proportionnelle à trois longueurs. |
|
|
i9 |
|
:i |
IV) INFORMATIONS
« formation leçon » :
|
Travaux auto - formation. |
|
|||||
|
Corrigé |
||||||
V )
DEVOIRS ( écrits):
|
Devoir diagnostique L
tests. |
|
|
Devoir Auto
- formatif
(intégré au cours) |
|
|
Devoir
Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .
|
Leçon |
Titre |
|
|
|
|
1°) Les parallèles équidistantes. |
|
|
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
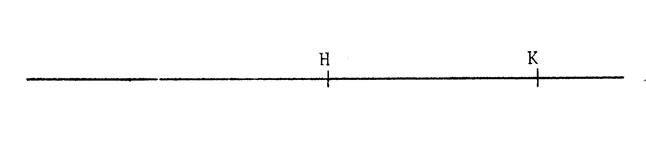
Rappel : Projection du milieu d’un segment. |
|
||||||||||||||||||||||||
|
|
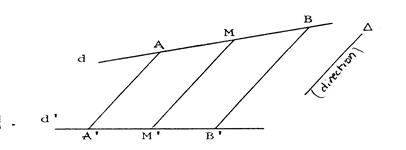
Dans la projection de la droite de direction « d » ,sur la droite « d ’ »suivant la direction
« Δ » , le segment [ AB ] a pour projeté …………………. Si « M » est le milieu de [ AB ]
,alors son projeté « M ’ »est le « milieu » de ……………… |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Projection d’une graduation régulière. |
|
||||||||||||||||||||||||
|
|
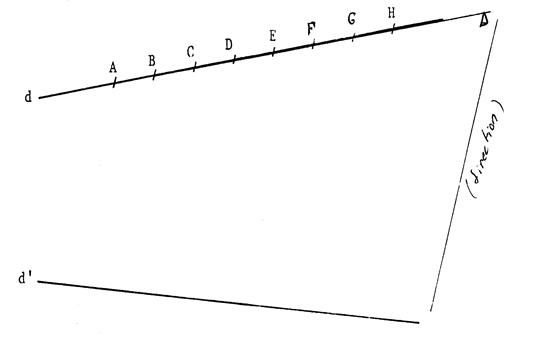
Sur la droite « d », les points
« A », « B »,
« C », « D », « E », « F »,
« G » et « H » détermine une graduation régulière. C'est-à-dire « AB = BC= CD= DE= EF = G H ». En projetant la droite « d » sur la droite « d ’ »
suivant la direction « Δ ». Les points « A », « B », « C », « D »,
« E », « F », « G » et « H » ont
respectivement pour projetés , les points « A ‘», « B ‘», « C’», « D’ »,
« E’ », « F ‘», « G’ » et « H’ » Activité n° 1 |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
§ Activité n° 2 Expliquez
pourquoi : les points « A ‘», « B ‘», « C’», « D’ »,
« E’ », « F ‘», « G’ » et « H’ » déterminent sur « d » une graduation
régulière ( C'est-à-dire «
A’B’ = B’C’= C’D’= D’E’= E’ F’ = G’
H’ ».) § Activité n° 3 Tracez une
droite dont la direction est « orthogonale » à « Δ » . On appellera « d ’’ » (lire « d » seconde), cette droite.
Appelez « A ‘’», « B ‘‘», « C ’’», « D ’’ », « E
’’ », « F ‘‘», « G ’’ » et « H ’’ » les points d’intersection de « d’’ »avec les parallèles. § Activité n° 4 Prouvez (montrez) que
la graduation ainsi déterminée sur « d’’ » est régulière. |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Rappel : On appelle « distance de deux
parallèles » la distance d’un
point de l’une à son projeté orthogonal sur l’autre. |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
On peut dire que « A ‘’ B ‘’» est la distance de la
droite ( A A
‘) à la droite ( B B ‘) et de même
« B ‘’ C’’ »est la distance de ………………….à
………………….. § Puisque « A’’B’’ = B’’C’’= C’’D’’= D’’E’’= E’’ F’’ = G’’ H’’ »on peut dire que les droites
parallèles que vous venez de tracer sont toutes à la même distance de leurs
voisines immédiates. On dit que ces droites sont des parallèles équidistantes. |
|
||||||||||||||||||||||||
|
|
§ Activité n° 4 :Tracez une droite coupant ces parallèles équidistantes. Vous pouvez démontrer comme précédemment que la graduation ainsi
déterminée sur cette droite est une graduation régulière. On
dira alors :. |
|
||||||||||||||||||||||||
|
|
Théorème : Si des parallèles déterminent une sécante des segments consécutifs de
même longueur, alors elles déterminent sur toute autre sécante des segments
consécutifs de même longueur. De telles parallèles sont appelées des parallèles équidistantes. |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
2) Partage d’un segment. |
|
||||||||||||||||||||||||
|
|
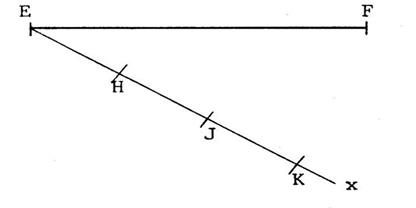
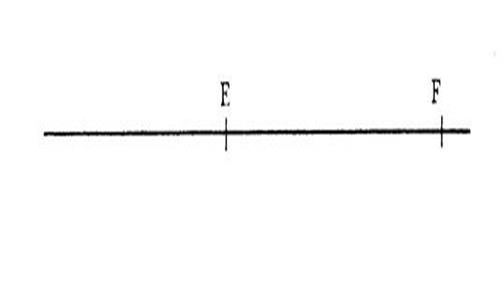
On veut partager le segment [ E F ] ci-contre
en 3 segments de même longueur. Activité n° 5 : a) Pour cela, on trace une demi droite « [ E
x » et sur cette demi-droite on place les points « H » ,
« J » , « K » tel que : « E H = H
J = J K » (
prendre un compas ) . b) Tracez ( K F) et, c)
Tracez une droite
passant par « H » et une autre droite passant par « J » ,ces droites étant
parallèles à ( K F). d) Nommez les points
« L » et « P » obtenus par ces droites qui coupent ( EF). D’après le théorème (sur
les parallèles équidistantes) , on peut dire
que « …
………= ………..= ……… » |
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
Activité n° 6 : |
|
|||||||||||||||||||||||||
|
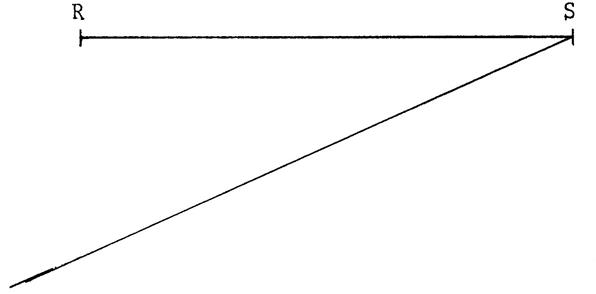
On vous demande de partager, comme ci-dessus, le segment [ R S ] en « 7 » segments de même longueur. ( ci-contre)
|
||||||||||||||||||||||||||
|
Posons un problème : n° 1 : |
|
|||||||||||||||||||||||||
|
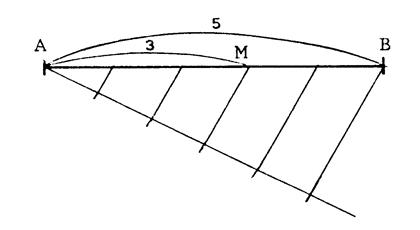
On vous donne un segment [ A B ] divisé en 5
parties égales.( Une graduation = Plaçons un point « M » sur « [AB] tel que « A M =
Pour ce faire ,il nous a suffi de partager [A
B ]en 5 segments de même longueur et d’en prendre « 3 »à partir de
« A ». Remarque : le partage de [AB] s’est fait comme précédemment. … |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
Remarque 1 : |
|
|||||||||||||||||||||||||
|
|
Sur le segment [ AB] il n’existe qu’un seul point
« M » tel que « A M = Mais : sur la droite (AB) , il en existe
un autre : le symétrique « M’ » de « M » par rapport
à « A ». (En effet, sur une
droite, il y a deux points à la même distance d’un point donné). |
|
||||||||||||||||||||||||
|
|
On a « A M = |
|
||||||||||||||||||||||||
|
|
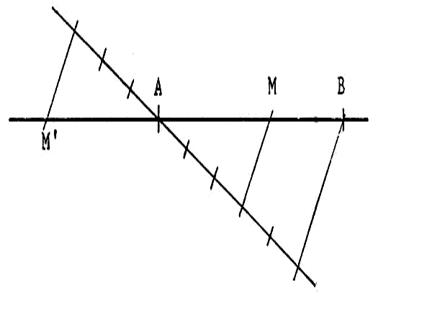
Remarque 2 : Pour « trouver » la position du point « M ’ » il suffit
d’observer le passage de la figure 1
à la figure 2 . .Il faut prolonger la 1/2 droite [ A x
,et reporter les graduations puis tracer une parallèle à celle passant par « M » ou « B ». |
|
||||||||||||||||||||||||
|
|
Figure 1 |
Figure 2. |
|
|||||||||||||||||||||||
|
|
« x » |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Activité n° 7 : |
|
||||||||||||||||||||||||
|
|
En vous aidant des activités précédentes, construisez les points
« S » et « S ’ »de la droite (EF) tels que :
|
|
||||||||||||||||||||||||
|
|
Posons le problème : n° 2 |
|
||||||||||||||||||||||||
|
|
On vous donne un segment [ AB ] , on vous demande
de construire un point « M » de ( AB ) tel que Puisque Donc « M » est à l’extérieur du segment [
AB] Voir
la construction ci-contre……
|
|
||||||||||||||||||||||||
|
|
Remarque : il existe un autre point « M’ »sur la
droite ( A B
) tel que C’est le symétrique de [ M
’] de « M » par rapport à
« A ». |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Activité n° 8 : |
|
||||||||||||||||||||||||
|
|
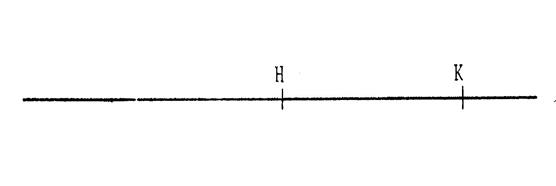
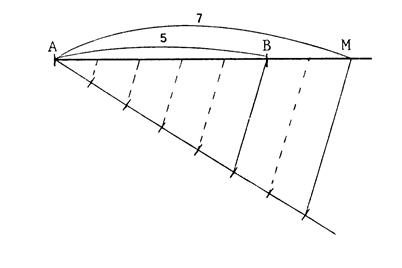
On donne le segment [ H K ]. Construisez les points « N » et « N’ » tels
que :
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
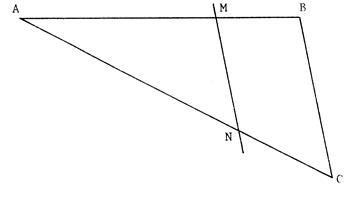
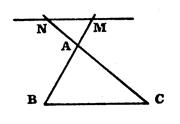
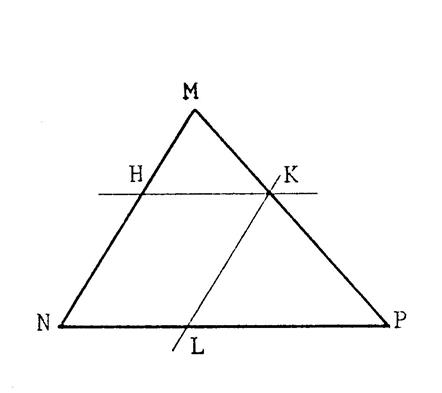
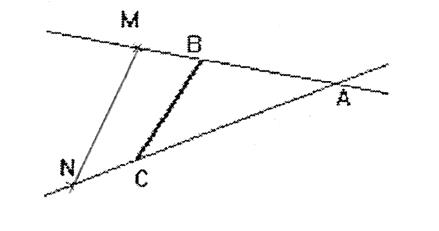
3°) Construction de points « M » et
« N » d’un triangle « ABC » tels que : |
|
||||||||||||||||||||||||
|
|
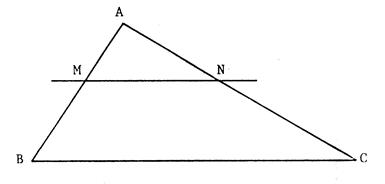
Etant donné un triangle, on veut déterminer la position d’un point
« M » sur [
AB ] tel que C'est-à-dire Pour cela, on procède comme au chapitre précédent « 2°) » : On utilise une demi-droite annexe [ A x ce qui permet de partager [ AB] en
« 5 » et en traçant des parallèles à ( BC ), on obtient le partage
de [AC] en « 5 ».
|
|
||||||||||||||||||||||||
|
|
Remarque 1 : Il n’est pas
nécessaire de tracer toutes les parallèles . Dés que la position du point
« M » est déterminé pour obtenir le point « N » il
suffit de tracer par « M » la « …………………. »
à «
………………….. ». |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Remarque 2 : (voir la
figure ci-dessus, comptez les graduations) On a On peut écrire aussi : Ou encore :
|
|
||||||||||||||||||||||||
|
|
Activité n° 9 |
|
||||||||||||||||||||||||
|
|
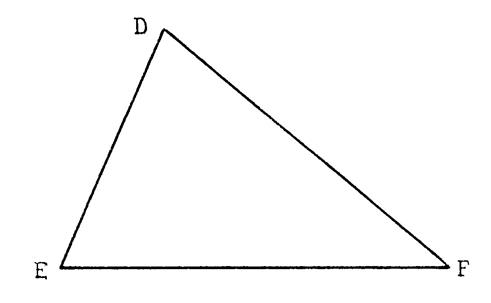
Soit la figure ci -contre, On vous donne un triangle « DFE ». Déterminez le point « P » sur [ DE
] et le point « R » sur [DF] Tels que Ayant placé le point « P » sur [ DE
] pour obtenir le point « R » sur [ DF ] il suffit de tracer par « P » la
………………………………..(EF)….
|
|
||||||||||||||||||||||||
|
|
Activité n° 10 |
|
||||||||||||||||||||||||
|
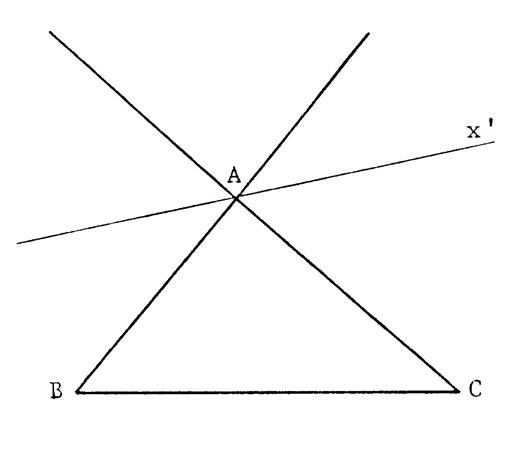
|
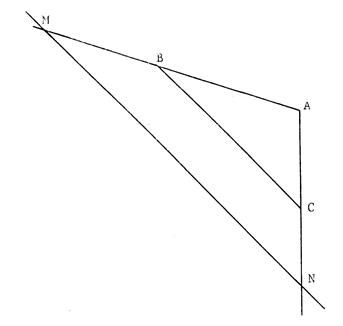
Ci-contre, on vous donne un
triangle « ABC » Déterminé le point « N » sur ( AB )
non situé sur [ AB ] Et le « M » sur ( AC ) non situé
sur [ AC ] tels que :
Utilisez la droite ( x x’ )
|
|
||||||||||||||||||||||||
|
|
Activité n° 10 |
|
||||||||||||||||||||||||
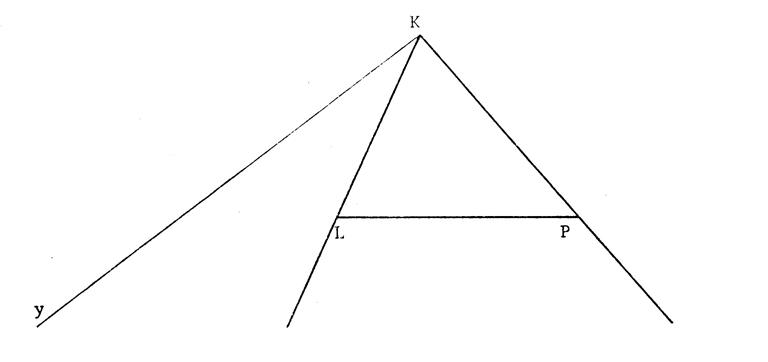
|
|
Ci-contre un triangle « KLP ». Déterminez le point « T » sur [ K L
. et le point « F » tels
que :
Utilisez la demi-droite annexe : [ K y.
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
4°) Expérimentation sur des triangles quelconques . |
|
||||||||||||||||||||||||
|
|
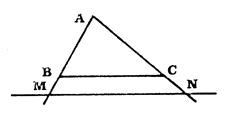
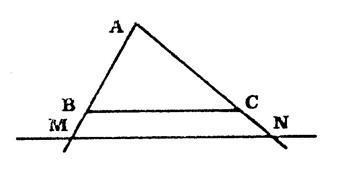
Voici des triangles « ABC » quelconques « a » ; « b » , « c » et « d » .. |
|
||||||||||||||||||||||||
|
|
Dans chacun des cas, une parallèle à (BC) coupe ( AB
) en « M » et ( AC ) en « N ». Mesurez ( en mm) les longueur « AB »
, « AC » , » « AM » , « MB » ,
« AN » et « NC » . Complétez le tableau après
avoir calculé les quotients ( à 10 -2 prés ) |
|
||||||||||||||||||||||||
|
|
Figure « a » |
Figure « b » |
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
Figure « c » |
Figure «d » |
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
Activité 11 |
|
||||||||||||||||||||||||
|
|
|
Mesures |
Rapports. |
|
||||||||||||||||||||||
|
|
Triangle. |
AB |
AC |
AM |
MB |
AN |
NC |
|
|
|
|
|
|
|
||||||||||||
|
« a » |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
« b » |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
« c » |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
« d » |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
« e » |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
« e » faite de même avec un triangle de votre choix …. |
|
||||||||||||||||||||||||
|
|
Bien que vos mesures ne soient pas parfaites, vous constatez que
certains quotients sont apparemment égaux et cela pour n’importe quel
triangle. Ecrivez ces égalités. |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Ces constations vous suggèrent la propriété suivante : Pour tout triangle « ABC », « M » étant un point
de ( AB) et « N » un point ( AC)
si : |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
5°) Théorème de Thalès. |
|
||||||||||||||||||||||||
|
|
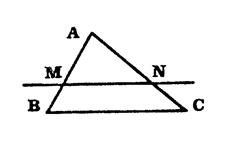
On donne un triangle « ABC » et une droite parallèle à ( BC ) qui coupe
respectivement ( AB ) et ( AC ) en
« M » et « N ». Ci-dessous les trois cas de figures possibles. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Vous avez vu au chapitre « 3 » et « 4 » que dans
cette situation on peut écrire :
Cette propriété est connue sous le nom de « Théorème de Thalès. ( nous ne ferons pas la démonstration à ce niveau ) |
|
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
Dans tout triangle « ABC » , « M » étant un point
de (AB) et « N » un point de ( AC) , si ( MN) est parallèle à ( B C
) alors les points « A » , « B » , « M »
déterminent sur ( AB) des segments dont les longueurs sont proportionnelles
aux longueurs des segments correspondants déterminés respectivement par
« A » , « C » , « N » sur ( AC) .
(voir
ci-dessous) |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Remarque : Les points
« A », « C », « N » sont les projetés
respectifs des points : « A » ,
« B » , « M » dans la projection de ( AB) sur (AC)
suivant la direction des parallèles ( BC ) et ( MN) |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Question :
Comment établir les rapports
égaux ? ou autrement
dit : Comment faire pour
écrire les quotients égaux ? |
|
||||||||||||||||||||||||
|
|
Prenons un exemple ci-dessus , soit le
triangle « ABC », ( BC) et ( MN) parallèles. On vous donne par exemple le rapport :
|
|
||||||||||||||||||||||||
|
|
Constat 1 : Les points « M » , « A »
, « B » sont des points appartenant à la droite ( AB) et les
points correspondants sont situés sur : …………………….. On doit penser à la projection : ( le
symbole Par
convention : On remplacera
l’expression « a pour image » par le
dessin : Aussi la projection de : |
|
||||||||||||||||||||||||
|
|
|
A |
On a alors : |
|
|
|||||||||||||||||||||
|
|
|
B |
|
|
||||||||||||||||||||||
|
|
|
M |
|
|
||||||||||||||||||||||
|
|
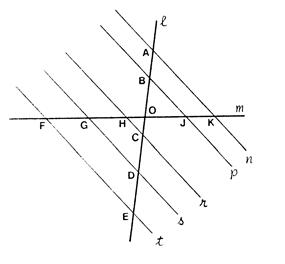
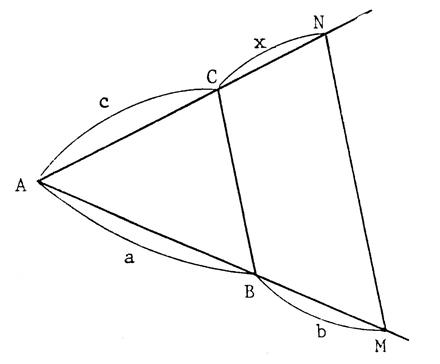
Activité n° 12 On vous donne deux droites « L »
et « m » se coupant en « O ». « n » , « p »,
« r » , « s » , « t » sont des droites
parallèles qui coupent « L »
et « m » en des points nommés sur la figure ci-contre. Complétez les égalités : |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Activité n° 13 |
|
||||||||||||||||||||||||
|
|
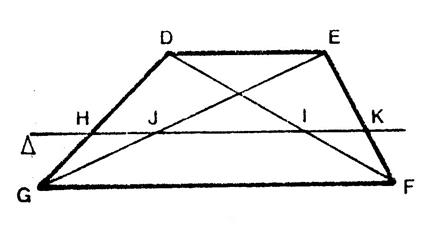
« DEFG » est un trapèze de base [ DE
] et [ FG ]. « Δ » est une droite parallèle aux bases
, coupe les droites ( DG) , ( DF), ( EG) , ( EF) en « H »,
« I » , « J » , « K ». On vous demande d’écrire trois quotients égaux à :
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Activité n° 14 |
Pré requis : le calcul : « la quatrième
proportionnelle » |
|
|||||||||||||||||||||||
|
|
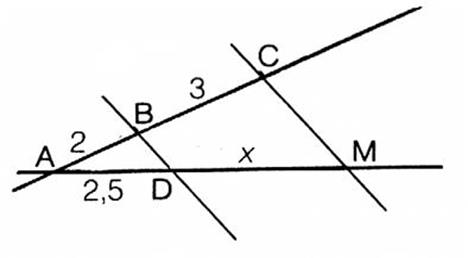
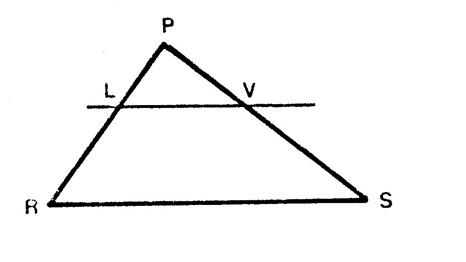
Un triangle « PRS »est
tel que « PR = 64 mm» et
« PS = 80 mm ». « L » est un point de [ PR ] tel que « PL = 24 mm ». Par « L » on trace la parallèle à la droite ( RS) qui
coupe ( PS) en « V ». Calculez la longueur PV. Corrigé :
On choisit l’égalité :
Il reste à effectuer le calcul : « la quatrième
proportionnelle » ( voir aussi dans cette
fiche le chapitre « 7 »)
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Activité n° 15 |
|
||||||||||||||||||||||||
|
|
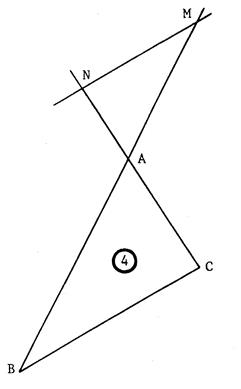
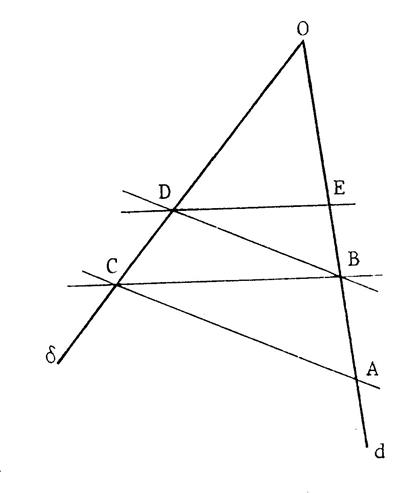
Deux droites (sécantes) « d » et « δ » se
coupent en « O ». « A » et « B » sont deux points de
« d ». Par les points « A » et « B » on trace deux
parallèles qui coupent respectivement
« δ » en
« C » et « D » . Par « D » on trace la parallèle à ( BC)
qui coupe « d » en « E ». On démontre que : Hypothèse :……………………………….. Conclusion : …………………………………
|
|
||||||||||||||||||||||||
|
|
Démonstration : Dans le triangle « OBD » , ( AC)
est parallèle à ( DB) ; donc ,
grâce au théorème de Thalès , Dans le triangle «
OBC » , ( CB) est parallèle à ( DE ) ;
donc , grâce au théorème de Thalès , On en déduit que : |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Activité n° 16 |
Cet
exercice demande de maitriser les rapports proportionnels.. |
|
|||||||||||||||||||||||
|
|
On vous donne un triangle « MNP ». Une parallèle à ( NP) coupe [ MN
] en « H » et [ MP] en « K ». « MH = 28 mm» , « MN =
77 mm» , « KP = 56 mm » 1°) Calculez “MK” Corrigé :
|
|
||||||||||||||||||||||||
|
|
2° ) On trace par “K” la parallèle à ( MN)
qui coupe ( NP) en “L” sachant que « NP = 99 mm , Calculez
« PL ». Corrigé : MP= MK + KP = 56 + 32 = 88 |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
6 °)
Quatrième proportionnelle à trois longueurs. |
(voir cours sur : » la quatrième
proportionnelle ») |
|
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
On vous donne 3 segments dont les longueurs sont « a » , « b » « c ». On se propose de construire le segment de longueur « x »,
tel que « x » soit la quatrième proportionnelles à « a » , « b » « c ». C'est-à-dire :
|
|
||||||||||||||||||||||||
|
|
Pour cela nous traçons un triangle « ABC » |
|
||||||||||||||||||||||||
|
|
Tel que « AB = a » et « AC= c » Plaçons sur [ AB un point « M » tel que « BM=
b » Traçons par « M » la parallèle à ( BC). Elle coupe ( AC ) en « N » Grâce au théorème de Thalès on a alors C'est-à-dire : La longueur du segment [ CN ] est la longueur cherchée.
|
|
||||||||||||||||||||||||
|
|
Remarque : vous pouvez imaginer d’autres façons de faire la
figure. |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
Activité n° 17 |
|
||||||||||||||||||||||||
|
|
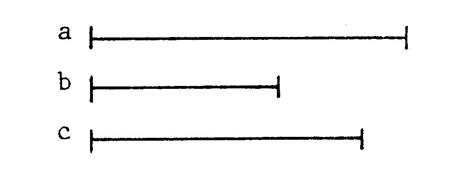
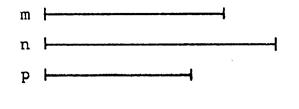
Construire un segment dont la longueur est la quatrième
proportionnelle des longueurs « m », « n »,
« p » des segments ci-dessous.
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
Leçon |
Titre |
|
N° |
TRAVAUX d ’ AUTO - FORMATION
sur THALES |
|
TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE |
|
1°) Enoncer le théorème de Thalès.
2°) Enoncer la propriété de Thalès.
3°) Enoncer la réciproque de Thalès.
|
|
Série 1 :
|
Exercice
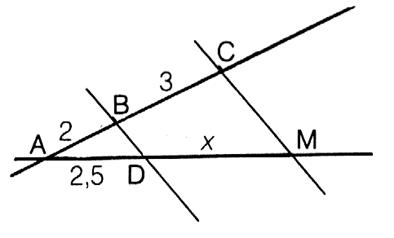
1 :
( 3 pts.)
On donne
( en cm) : AM = 7 ; AB =
3 ; AN = 9 ; AC = 5 Les droites BC et NM sont-elles parallèles ? justifier |
|
|
Série 2
|
1°) quelle est la mesure de AM par rapport à AB |
|
|
|
|
|
2°) Calculer l'abscisse du point A |
|
|
|
|
|
3°) Calculer la longueur "x" |
|
|
|
|