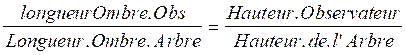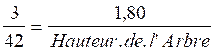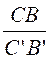Pré requis
|
|||||||||||||||
|
Les
triangles semblables et homothétiques |
|||||||||||||||
|
L’homothétie
|
|||||||||||||||
|
|
|||||||||||||||
|
ENVIRONNEMENT
du dossier |
|
||||||||||||||
|
Objectif précédent : |
Objectif suivant : |
2°)Liste des objectif de cours sur Thalès 3°) Liste de cours de géométrie
plane. |
|||||||||||||
|
|
|||||||||||||||
|
|
DOSSIER : THALES |
|
|||||||||||||
|
|
1.
Théorème 2.
Réciproque du théorème
3.
Propriétés
de Thalès |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
5.
|
|||||||||||||||
|
COURS |
Corrigé
Contrôle |
Corrigé
évaluation |
|||||||||||||
|
|
|
|
|||||||||||||
|
|
:test :
Evaluation diplômante :Contrôle Continu : Thalès
|
|
|||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Ce qu ‘il faut savoir sur le théorème : ce théorème rend compte , en
fait , de propriétés à peu prés évidente qu’ont des
droites parallèles quand elles en coupent
deux ou plusieurs autres. La notion fondamentale qui est en jeu est celle de
« rapport » , et le théorème énonce l ’
égalité de deux rapports , donc met en jeu une « proportion ». (Stella
BARUK ,
Dictionnaire des Mathématiques élémentaires ;ed.
Seuil , page 1193) THALES
et le THEOREME de THALES Qui est « THALES » ? Thalès de Millet. Il vécut environ 600 ans avant J.C. Il est né en Grèce au VIIième
siècle avant J.C. . Mathématicien et philosophe grec ,
on lui attribua la première mesure « exacte » du temps, il aurait
apporté d ’ Egypte en Grèce les fondements de la géométrie. Travaillant sur les lignes
(droites, cercles ,angles ) il donna son point de départ à la
géométrie pure :il fut le premier à démontrer que le diamètre d’un
cercle partage celui-ci en deux parties égales , que tout angles inscrit dans
un demi cercle est droit , que deux angles opposés
par le sommet sont égaux . On suppose qu’il fut le premier à bâtir des démonstrations
élémentaires à partir d ’ axiomes. Quelques définitions : « Axiomes » un axiome est un énoncé évident par lui même et donc non susceptible d’être démontré. Exemples
d’axiomes d ’ Euclide : On
peut ajouter ou soustraire la même quantité à deux quantités égales .Les
quantités obtenues sont alors égales. Deux
quantités égales à la même quantité sont égales entre elles. Postulat : Le postulat est un principe premier , indémontrable ou non démontré , dont l’admission
est nécessaire pour établir une démonstration. Exemples
de postulats d’Euclide. Par deux points passe une droite. Un
cercle est déterminé par la connaissance de son centre et de son rayon. Tous
les angles droits sont égaux . Par
un point extérieur à une droite , on peut mener une et une seule droite parallèle à cette droite. Définition de « Théorème » :
du latin theorema , du grec théôrêma ,
« ce qu ‘on peut contempler » d’après le Littré :
« théorème » : terme didactique, consiste en
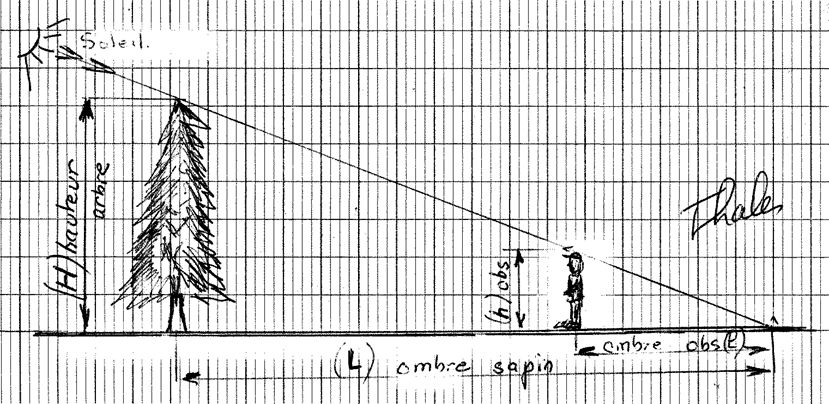
« toute proposition qui a besoin d’une démonstration pour devenir évidente » A quoi sert le théorème de THALES. Exemple : Calculer la hauteur d’un arbre : |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Par soleil : On connaît la hauteur de l’Observateur ( On mesure la longueur de
l’ombre de l ’
arbre au sol. L’observateur se
place debout au point de rencontre (affleurement de la tête) avec l’ombre
« portée », on mesure la distance qui sépare l’Observateur et le point de rencontre des ombres (point
le plus éloigné de l’ombre de l’arbre ) : On établit la relation de
proportion :
si hauteur de l’observateur = 1,80
; Ombre Observateur 3
m : ;longueur de l’ombre de l’arbre nous remplaçons dans la relation de proportion :
Calcul de la quatrième
proportionnelle :
hauteur de l’arbre = 1,80 fois 42 divisé par 3 Conclusion : l’arbre à pour
hauteur approximative : |
|
|||||||||||||
|
|
Théorème
de Thalès :
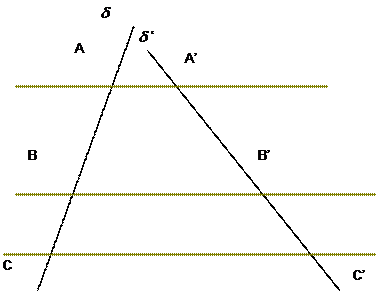
(énoncés équivalents). Premier énoncé : Si des parallèles découpent sur
chacune des sécantes D1 et D2 , des segments
respectivement de longueur l1 ;
l2 ; l’1 et l’2 , les quatre longueurs (ainsi obtenues)
sont en « proportion ». |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||
|
D1 l1 l’1 l2 l’2 D2 |
Une
fois les segments , sur chaque droite sécante,
nommés il suffit d’établir l’égalité des
rapports :
- à partir des projections (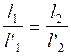 )
)
- à partir des proportions des
longueurs des segments : (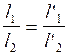 )
)
Deuxième
énoncé :
info :
d : lire « delta »
AB :
lire « longueur du segment d’origine A d’extrémité B »
BC :
lire « longueur du segment d’origine B d’extrémité C »
AC :
lire « longueur du segment d’origine A d’extrémité C »
A’B’ :
lire « longueur du segment d’origine A’ d’extrémité B’ »
B’C’ :
lire « longueur du segment d’origine B’ d’extrémité C’ »
A’C’ :
lire « longueur du segment d’origine A’ d’extrémité C’ »
Si deux segments d ’
« une droite » d :
ont leurs longueurs dans un certain « rapport » ,
des parallèles reproduisent ce rapport sur n’importe quelle autre droite qui
les coupe
en
particulier :
|
|
Si A,B,C,
sont trois points d’une droite. d , A’ ; B’ et C’ les
points correspondants par parallèles
sur une droite d ‘ , on peut , pour chacun des six rapports de longueurs
déterminés par la position des points A,B, C , écrire qu
‘il est égal au rapport déterminé par les longueurs correspondantes sur d ‘
, soit :
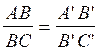 ou
ou 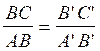
*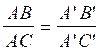 ou
ou 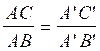
*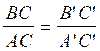 ou
ou 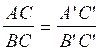
*si problème de compréhension voir « les
triangles homothétiques »
Le théorème est un énoncé
« vrai » dans une théorie mathématique donnée .Leur vérité a été établie , ils sont à redémontrer.(et non pas « à
démontrer »)
|
RECIPROQUE DU THEOREME de THALES. |
|
Rappel : Traduction de ![]() : lire « mesure algébrique du bipoint AB »
: lire « mesure algébrique du bipoint AB »
Deux formes :
Première
forme :
Pour montrer qu’un point M’ est le projeté d’un point M sur une droite « D’ »
suivant un droite de direction donnée « d ».
Soit la description de la représentation graphique suivante :
Une droite graduée « D » et
deux points A et B (A et B étant
différents).
Une droite graduée « D’ » sur
laquelle sont tracées les projetés
respectives A’ et B’ selon une droite de direction donnée « d »
|
|
||||||||||||
Soit
un point « M » de la droite « D » et « M’ » le point de la droite
« D’ »,
Si « M » est le
point de « D » et
« M’ » le point de « D’ » , si l’
on vérifie « l’égalité vraie » de la proportion suivante : 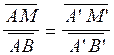
alors on conclut que le
point « M » de la droite «D » est le projeté du
point « M » sur la droite
« D’ » selon la direction « d ».
et donc que : ![]() =
= 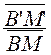 =
= 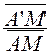
PROJECTION DU MILIEU D’UN SEGMENT
Si B est milieu du segment [AM] , alors ![]() = -1
= -1
Comme 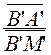 =
= ![]() on obtient
on obtient 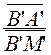 = -1 et B’
est le milieu du segment [A’C’]
= -1 et B’
est le milieu du segment [A’C’]
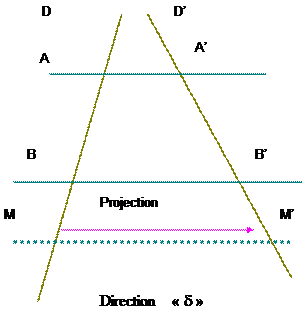
Deuxième forme :
Pour montrer qu
‘ une droite ( MM’) est parallèle à deux autres droites AA’ et BB’.
Soit la description de la représentation graphique suivante :
Une droite graduée « D » et
une droite graduée « D’ »
sécantes .
Deux droites «d » et
«d ‘ » strictement
parallèles ,coupant respectivement la
droite « D » au x points A et B
et « D’ » en A’ et B’ .
Soit un point
« M » de la droite
« D » et « M’ » le
point de la droite « D’ »,
d’
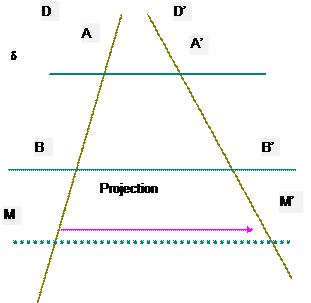
Si « M » est le
point de « D » et
« M’ » le point de « D’ » , si
l’on établit la proportion tels que :
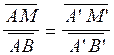 et que l’on vérifie
que « l’égalité est vraie »
(avec les nombres données),
alors la droite ( MM’) est parallèle aux
droites passant respectivement par les points AA’ et les points BB’.
et que l’on vérifie
que « l’égalité est vraie »
(avec les nombres données),
alors la droite ( MM’) est parallèle aux
droites passant respectivement par les points AA’ et les points BB’.
A D B C F E D1 D2 D3 D1 ; D2 ; D3 sont
// AB = 18 mm ; BC = 14 mm ; DE = Calculer la longueur DF![]()
![]()
![]()
![]()

|
Relation mathématique:
On remplace dans les relations les lettres par les valeurs données: On établit deux proportions , dans les quelles
on connaît 3 valeurs sur quatre 1°) On calcule la quatrième
proportionnelle: EF = (14 fois 13,5)
divisé 18 EF = 10,5 2°) On calcule la quatrième proportionnelle DF =
(32 fois 13,5)divisé par 18 DF = 24 |
II ) Dans la figure ci - dessous
, comparer les triangles :
ABC et A B’C’ ; (BC ) // ( B’C’ )
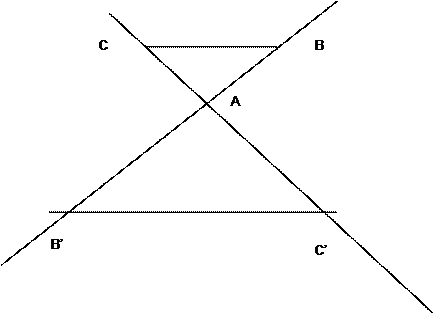
BC = 2,8 cm
; B’C’ = 4 cm ; AC = 2 cm ; rectangle en A
SOLUTION :
Calculer AB ; AB’ ; AC’
|
Transformer
le dessin : (rotation) |
|
|
Faire une rotation du triangle ACB dans le
sens des aiguilles d'une montre autour du point A ( point A est centre de rotation); Après la rotation on doit obtenir BC // B'C' ( le point B doit se trouver sur le segment B'A ) |
|
|
Constat : les triangles ABC et AB'C' sont
homothétiques ; il existe donc un rapport d' homothétie
: On prend deux rapports donc on connaît 3
valeurs sur 4
|
Les rapports homothétie sont (ils n'y a pas d'ordre
) On
remplace dans les rapports les valeurs que l'on nous donne.
AC' = (4 fois 2 ) divisé
par 2,8 AC' »2,8571429 (voir "arrondir"
) |
|
Nous
connaissons : AC' = 2,86 ; et B'C'= 4 , le triangle est rectangle
en A Nous
pouvons chercher AB' par Pythagore: (B'C')2 = (B'A)2+ (AC')2 42 =
(B'A)2+ (2,86)2 après transformation: 42 - (2,86)2
= (B'A)2 ou (B'A)2 = 42
- (2,86)2 (B'A)2 =
16 -8,1796 (B'A)2 =7,8204
B'A » 2,7964978 B'A » 2,80 à 0,001 prés On peut maintenant calculer la valeur de AB :
à partir des rapports précédemment établis :
On
remplace dans les rapports les valeurs que l'on nous donne.
ainsi:
AB = (2,8 fois 2,8)divisé
par 4 AB =
1,96 |
|
|
Autres applications : Thalès et le triangle |
||||
Cas général:
|
||||
|
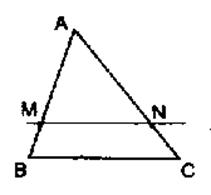
Si dans un triangle A BC , une parallèle à un segment [
BC] coupe un segment [ AB]
en M et un segment [ AC
]en un point N alors on a
:
|
|
|||
|
Cas particulier
|
|
||
|
Les milieux : Dans un triangle , la droite qui passe par le milieu d’un côté et qui
est parallèle à un autre côté coupe le troisième en son milieu . |
|
|
|
|
Propriété des milieux des côtés : Si M est milieu du segment AB , la parallèle à la droite ( BC)
menée par M coupe la droite (AC) en N milieu de [AC] ( voir projection du milieu d’un segment ) . Réciproquement : si N et milieu de [AC],
On énonce : Si M est le milieu du côté [AB]
d’un triangle ABC. Le point N du segment [AC
] est milieu de [AC] si et seulement si la droite ( MN ) esr parallèle à la droite
( BC ) Si M , N , P sont les milieux
des côtés [AB] [BC ] [CA]
du triangle ABC , que peut-on
dire des directions des côtés du
triangle MNP ? ( voir info plus ++++) |
|
||
|
|
Enoncé le théorème de Thalès ;
vous vous aidez d’un dessin pour « expliquer ».
EVALUATION
|
I ) |
|
A D B C F E D1 D2 D3 D1 ; D2 ; D3 sont
// AB = 18 mm ; BC = 14 mm ; DE = Calculer la longueur DF![]()
![]()
![]()
![]()

II ) Dans la figure ci - dessous
, comparer les triangles :
ABC et A B’C’ ; (BC ) // ( B’C’ )
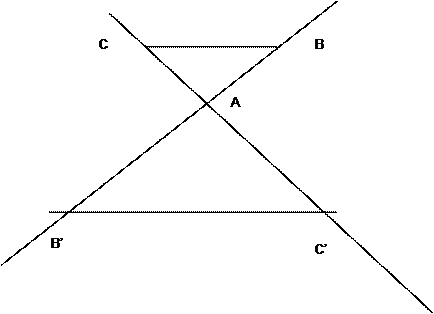
BC = 2,8 cm
; B’C’ = 4 cm ; AC = 2 cm ; rectangle en A
Calculer AB ; AB’ ; AC’