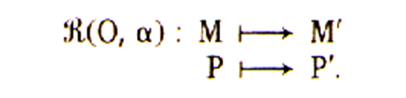Pré requis:
|
Cercle |
||||||||||
|
Angle |
||||||||||
|
ENVIRONNEMENT du dossier: |
||||||||||
|
Index : |
Objectif précédent : |
|||||||||
|
LES ROTATIONS par rapport à un point |
||||||||||
|
|
|
|
||||||||
|
|
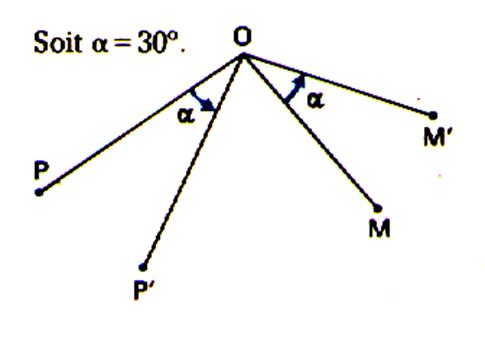
1. Définition |
|
||||||||
|
|
2. Notation |
|
||||||||
|
|
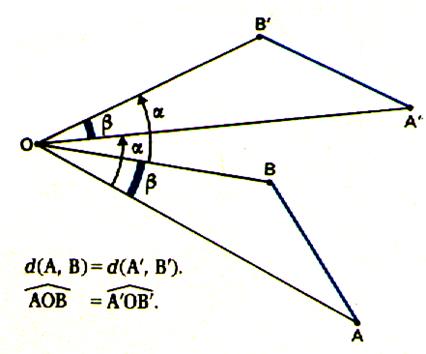
3. Propriétés |
|
||||||||
|
|
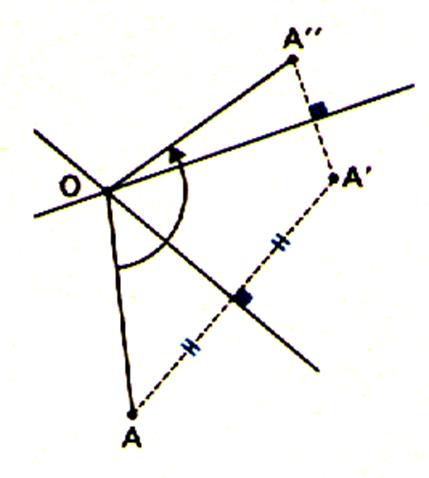
4. Théorème |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
|
TEST |
COURS |
Interdisciplinarité |
|
|||||||